(Created page with "3) a) 270x222px <math> \begin{align*} \text{\underline{BC's}:}& &E_{1t}&= E_{2t}\\ & &D_{1n}-D_{2n}&=\rho_s \end{align*} </math> <math> \begin{e...") |
|||
| Line 23: | Line 23: | ||
b) | b) | ||
| − | [[Image:pot. | + | [[Image:pot.jpg|Alt text|270x222px]] |
<math> | <math> | ||
Latest revision as of 18:39, 18 June 2017
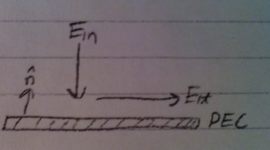
3)
a)
$ \begin{align*} \text{\underline{BC's}:}& &E_{1t}&= E_{2t}\\ & &D_{1n}-D_{2n}&=\rho_s \end{align*} $
$ \begin{equation*} \text{In PEC, $\bar{E}=0$ so:} \left\{\begin{aligned} E_{1t}&=E_{2t}=0 \\ D_{1n}&=\rho_s \end{aligned} \right. \end{equation*} $
only normal component of $ \bar{D} $ is non-zero, implying only $E_n$ exists in the region above the PEC due to the charge distribution on the PEC surface.
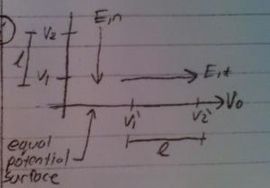
b)
$ \begin{align*} \quad V'_2-V'_1&=-\int_1^2\bar{E}_{1t}\cdot d\bar{l}&&\\ \quad V_0-V_0&=-E_{1t}(l)=0&&\\ \longrightarrow &\boxed{E_{1t}=0}&&\\ \quad V_2-V_1&=-E_{1n}(l)\neq0&&\\ &\boxed{E_{1n}\neq0}\longleftarrow \text{only normal component\\ is not zero} \end{align*} $