Latest revision as of 20:52, 24 April 2017

ECE Ph.D. Qualifying Exam

Fields and Optics (FO)

Question 1: Statics 1

August 2013

Question 1

Solution

Click here to view student answers and discussions

Question 2

Solution

Click here to view student answers and discussions

Question 3

Solution

Click here to view student answers and discussions

Back to ECE Qualifying Exams (QE) page

@@ Line 20: / Line 20: @@
 ----
 ----
-==Question==
+==Question 1==
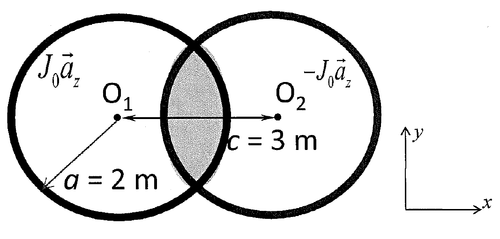
 [[Image:Q1FO12013.png|Alt text|500x500px]]
-=Solution=
-write it here
-==Question==
+[[Image:Q1FO12013D.png|Alt text|200x200px]]
-'''Part 1. '''
-Consider <math class="inline">n</math> independent flips of a coin having probability <math class="inline">p</math> of landing on heads. Say that a changeover occurs whenever an outcome differs from the one preceding it. For instance, if <math class="inline">n=5</math> and the sequence <math class="inline">HHTHT</math> is observed, then there are 3 changeovers. Find the expected number of changeovers for <math class="inline">n</math> flips. ''Hint'': Express the number of changeovers as a sum of Bernoulli random variables.
+=Solution=
+:'''Click [[ECE_PhD_QE_FO_2013_Problem1.1|here]] to view student [[ECE_PhD_QE_FO_2013_Problem1.1|answers and discussions]]'''
-:'''Click [[ECE_PhD_QE_CNSIP_2013_Problem1.1|here]] to view student [[ECE_PhD_QE_CNSIP_2013_Problem1.1|answers and discussions]]'''
+==Question 2==
-----
+[[Image:Q2FO12013.png|Alt text|500x500px]]
-'''Part 2.'''
-Let <math>X_1,X_2,...</math> be a sequence of jointly Gaussian random variables with covariance
+=Solution=
+:'''Click [[ECE_PhD_QE_FO_2013_Problem2.1|here]] to view student [[ECE_PhD_QE_FO_2013_Problem2.1|answers and discussions]]'''
-<math>Cov(X_i,X_j) = \left\{ \begin{array}{ll}
+==Question 3==
- {\sigma}^2, & i=j\\
+[[Image:Q3FO12013.png|Alt text|500x500px]]
- \rho{\sigma}^2, & |i-j|=1\\
-, & otherwise
-  \end{array} \right.</math>
-Suppose we take 2 consecutive samples from this sequence to form a vector <math>X</math>, which is then linearly transformed to form a 2-dimensional random vector <math>Y=AX</math>. Find a matrix <math>A</math> so that the components of <math>Y</math> are independent random variables You must justify your answer.
+[[Image:Q3FO12013D.png|Alt text|500x500px]]
-:'''Click [[ECE_PhD_QE_CNSIP_2013_Problem1.2|here]] to view student [[ECE_PhD_QE_CNSIP_2013_Problem1.2|answers and discussions]]'''
+=Solution=
-----
+:'''Click [[ECE_PhD_QE_FO_2013_Problem3.1|here]] to view student [[ECE_PhD_QE_FO_2013_Problem3.1|answers and discussions]]'''
-'''Part 3.'''
-Let <math>X</math> be an exponential random variable with parameter <math>\lambda</math>, so that <math>f_X(x)=\lambda{exp}(-\lambda{x})u(x)</math>. Find the variance of <math>X</math>. You must show all of your work.
-:'''Click [[ECE_PhD_QE_CNSIP_2013_Problem1.3|here]] to view student [[ECE_PhD_QE_CNSIP_2013_Problem1.3|answers and discussions]]'''
-----
-'''Part 4.'''
-Consider a sequence of independent random variables <math>X_1,X_2,...</math>, where <math>X_n</math> has pdf
-<math>\begin{align}f_n(x)=&(1-\frac{1}{n})\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{1}{2\sigma^2}(x-\frac{n-1}{n}\sigma)^2]\\
-&+\frac{1}{n}\sigma exp(-\sigma x)u(x)\end{align}</math>.
-Does this sequence converge in the mean-square sense? ''Hint:'' Use the Cauchy criterion for mean-square convergence, which states that a sequence of random variables <math>X_1,X_2,...</math> converges in mean-square if and only if <math>E[|X_n-X_{n+m}|] \to 0</math> as <math>n \to \infty</math>, for every <math>m>0</math>.
-:'''Click [[ECE_PhD_QE_CNSIP_2013_Problem1.4|here]] to view student [[ECE_PhD_QE_CNSIP_2013_Problem1.4|answers and discussions]]'''
 ----
 [[ECE_PhD_Qualifying_Exams|Back to ECE Qualifying Exams (QE) page]]

Difference between revisions of "ECE PhD QE Fields Optics 2013" - Rhea

Latest revision as of 20:52, 24 April 2017

Contents

Question 1

Solution

Question 2

Solution

Question 3

Solution

Alumni Liaison