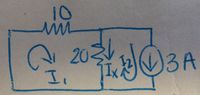| (7 intermediate revisions by the same user not shown) | |||
| Line 21: | Line 21: | ||
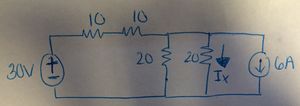
Determine the value of <math> I_x </math> using superposition. | Determine the value of <math> I_x </math> using superposition. | ||
| − | [[File: | + | [[File:ECE201 P2.jpg|300px|center]] |
---- | ---- | ||
| Line 31: | Line 31: | ||
Let's find <math> I_x </math> first by deactivating the voltage source as seen in the picture below. | Let's find <math> I_x </math> first by deactivating the voltage source as seen in the picture below. | ||
| − | [[File: | + | [[File:ECE201_P3_2.jpg|200px|center]] |
We can find <math> I_x </math> by using loop analysis. The left loop can be <math> I_1 </math> and the right loop can be <math> I_2 </math>.<br /> | We can find <math> I_x </math> by using loop analysis. The left loop can be <math> I_1 </math> and the right loop can be <math> I_2 </math>.<br /> | ||
When doing loop analysis we can come up with the following equation:<br /> | When doing loop analysis we can come up with the following equation:<br /> | ||
<math>\begin{align} | <math>\begin{align} | ||
| − | I_1: | + | I_1: |
10*I_1 + 20(I_1 - I_2) = 0\\ | 10*I_1 + 20(I_1 - I_2) = 0\\ | ||
30*I_1 = 20*I_2\\ | 30*I_1 = 20*I_2\\ | ||
| − | I_2: | + | I_2: |
I_2 = 3A\\ | I_2 = 3A\\ | ||
\end{align} | \end{align} | ||
| − | </math> | + | </math><br /> |
| − | After finding <math> I_1 </math> and <math> I_2 </math> we can find <math> I_x </math>. | + | After finding <math> I_1 </math> and <math> I_2 </math> we can find <math> I_x </math>.<br /> |
<math>\begin{align} | <math>\begin{align} | ||
I_x = I_1 - I_2\\ | I_x = I_1 - I_2\\ | ||
| Line 54: | Line 54: | ||
Now we need to do the same procedure but this time we will deactivate the current source; therefore, we will get the following circuit:<br /> | Now we need to do the same procedure but this time we will deactivate the current source; therefore, we will get the following circuit:<br /> | ||
| − | [[File:ECE201_P3_3.jpg| | + | [[File:ECE201_P3_3.jpg|200px|center]] |
We can use source transformation to turn the voltage source into the current then use current division to solve for <math> I_x </math>.<br /> | We can use source transformation to turn the voltage source into the current then use current division to solve for <math> I_x </math>.<br /> | ||
After doing source transformation we get the following circuit:<br /> | After doing source transformation we get the following circuit:<br /> | ||
| − | [[File:ECE201_P3_4.jpg| | + | [[File:ECE201_P3_4.jpg|200px|center]] |
Now use current division to find <math> I_x </math>.<br /> | Now use current division to find <math> I_x </math>.<br /> | ||
| Line 68: | Line 68: | ||
</math> | </math> | ||
| − | Finally, the last step would be to add up the two <math> I_x </math> | + | Finally, the last step would be to add up the two <math> I_x </math> values we obtained by deactivating the voltage and current sources. |
<math> I_x = -1 + 2</math><br /> | <math> I_x = -1 + 2</math><br /> | ||
<math> I_x = 1A</math><br /> | <math> I_x = 1A</math><br /> | ||
Latest revision as of 15:31, 2 May 2015
Superposition Practice
Practice question for ECE201: "Linear circuit analysis I"
By: Chinar Dhamija
Topic: Superposition
Question
Determine the value of $ I_x $ using superposition.
Answer
The circuit has two sources, a voltage and a current source. In order to find $ I_x $ we need to look at two instances.
1. Deactivate the voltage source (V = 0)
2. Deactivate the current source (I = 0)
Let's find $ I_x $ first by deactivating the voltage source as seen in the picture below.
We can find $ I_x $ by using loop analysis. The left loop can be $ I_1 $ and the right loop can be $ I_2 $.
When doing loop analysis we can come up with the following equation:
$ \begin{align} I_1: 10*I_1 + 20(I_1 - I_2) = 0\\ 30*I_1 = 20*I_2\\ I_2: I_2 = 3A\\ \end{align} $
After finding $ I_1 $ and $ I_2 $ we can find $ I_x $.
$ \begin{align} I_x = I_1 - I_2\\ I_x = 2 - 3\\ I_x = -1\\ \end{align} $
That is what we get for $ I_x $ if the voltage source is deactivated.
Now we need to do the same procedure but this time we will deactivate the current source; therefore, we will get the following circuit:
We can use source transformation to turn the voltage source into the current then use current division to solve for $ I_x $.
After doing source transformation we get the following circuit:
Now use current division to find $ I_x $.
$ \begin{align} I_x = \frac{1/10}{1/10 + 1/20} * 3\\ I_x = 2\\ \end{align} $
Finally, the last step would be to add up the two $ I_x $ values we obtained by deactivating the voltage and current sources.
$ I_x = -1 + 2 $
$ I_x = 1A $
Questions and comments
If you have any questions, comments, etc. please post them below
- Comment 1
- Answer to Comment 1
- Comment 2
- Answer to Comment 2