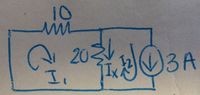| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Category: | + | [[Category:ECE201]] |
| + | [[Category:ECE]] | ||
| + | [[Category:ECE201Spring2015Peleato]] | ||
| + | [[Category:circuits]] | ||
| + | [[Category:linear circuits]] | ||
| + | [[Category:problem solving]] | ||
| − | = | + | =Superposition Practice= |
| + | <center><font size= 4> | ||
| + | '''Practice question for [[ECE201]]: "Linear circuit analysis I" ''' | ||
| + | </font size> | ||
| + | By: Chinar Dhamija | ||
| + | Topic: Superposition | ||
| − | + | </center><br /> | |
| + | ---- | ||
| + | ==Question== | ||
| + | Determine the value of <math> I_x </math> using superposition. | ||
| + | [[File:ECE201 P2.jpg|300px|center]] | ||
| + | ---- | ||
| + | ---- | ||
| + | ===Answer === | ||
| + | The circuit has two sources, a voltage and a current source. In order to find <math> I_x </math> we need to look at two instances.<br /> | ||
| + | 1. Deactivate the voltage source (V = 0)<br /> | ||
| + | 2. Deactivate the current source (I = 0)<br /> | ||
| − | [[ 2015 Spring ECE 201 Peleato|Back to 2015 Spring ECE 201 Peleato]] | + | Let's find <math> I_x </math> first by deactivating the voltage source as seen in the picture below. |
| + | [[File:ECE201_P3_2.jpg|200px|center]] | ||
| + | We can find <math> I_x </math> by using loop analysis. The left loop can be <math> I_1 </math> and the right loop can be <math> I_2 </math>.<br /> | ||
| + | When doing loop analysis we can come up with the following equation:<br /> | ||
| + | <math>\begin{align} | ||
| + | I_1: | ||
| + | 10*I_1 + 20(I_1 - I_2) = 0\\ | ||
| + | 30*I_1 = 20*I_2\\ | ||
| + | I_2: | ||
| + | I_2 = 3A\\ | ||
| + | \end{align} | ||
| + | </math><br /> | ||
| + | |||
| + | After finding <math> I_1 </math> and <math> I_2 </math> we can find <math> I_x </math>.<br /> | ||
| + | <math>\begin{align} | ||
| + | I_x = I_1 - I_2\\ | ||
| + | I_x = 2 - 3\\ | ||
| + | I_x = -1\\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | That is what we get for <math> I_x </math> if the voltage source is deactivated.<br /> | ||
| + | |||
| + | Now we need to do the same procedure but this time we will deactivate the current source; therefore, we will get the following circuit:<br /> | ||
| + | [[File:ECE201_P3_3.jpg|200px|center]] | ||
| + | |||
| + | We can use source transformation to turn the voltage source into the current then use current division to solve for <math> I_x </math>.<br /> | ||
| + | After doing source transformation we get the following circuit:<br /> | ||
| + | [[File:ECE201_P3_4.jpg|200px|center]] | ||
| + | |||
| + | Now use current division to find <math> I_x </math>.<br /> | ||
| + | <math>\begin{align} | ||
| + | I_x = \frac{1/10}{1/10 + 1/20} * 3\\ | ||
| + | |||
| + | I_x = 2\\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Finally, the last step would be to add up the two <math> I_x </math> values we obtained by deactivating the voltage and current sources. | ||
| + | <math> I_x = -1 + 2</math><br /> | ||
| + | <math> I_x = 1A</math><br /> | ||
| + | |||
| + | |||
| + | ---- | ||
| + | ==Questions and comments== | ||
| + | If you have any questions, comments, etc. please post them below | ||
| + | *Comment 1 | ||
| + | **Answer to Comment 1 | ||
| + | *Comment 2 | ||
| + | **Answer to Comment 2 | ||
| + | ---- | ||
| + | [[2015 Spring ECE 201 Peleato|Back to 2015 Spring ECE 201 Peleato]] | ||
| + | |||
| + | [[ECE201|Back to ECE201]] | ||
Latest revision as of 15:31, 2 May 2015
Superposition Practice
Practice question for ECE201: "Linear circuit analysis I"
By: Chinar Dhamija
Topic: Superposition
Question
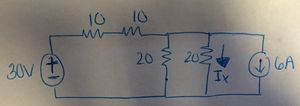
Determine the value of $ I_x $ using superposition.
Answer
The circuit has two sources, a voltage and a current source. In order to find $ I_x $ we need to look at two instances.
1. Deactivate the voltage source (V = 0)
2. Deactivate the current source (I = 0)
Let's find $ I_x $ first by deactivating the voltage source as seen in the picture below.
We can find $ I_x $ by using loop analysis. The left loop can be $ I_1 $ and the right loop can be $ I_2 $.
When doing loop analysis we can come up with the following equation:
$ \begin{align} I_1: 10*I_1 + 20(I_1 - I_2) = 0\\ 30*I_1 = 20*I_2\\ I_2: I_2 = 3A\\ \end{align} $
After finding $ I_1 $ and $ I_2 $ we can find $ I_x $.
$ \begin{align} I_x = I_1 - I_2\\ I_x = 2 - 3\\ I_x = -1\\ \end{align} $
That is what we get for $ I_x $ if the voltage source is deactivated.
Now we need to do the same procedure but this time we will deactivate the current source; therefore, we will get the following circuit:
We can use source transformation to turn the voltage source into the current then use current division to solve for $ I_x $.
After doing source transformation we get the following circuit:
Now use current division to find $ I_x $.
$ \begin{align} I_x = \frac{1/10}{1/10 + 1/20} * 3\\ I_x = 2\\ \end{align} $
Finally, the last step would be to add up the two $ I_x $ values we obtained by deactivating the voltage and current sources.
$ I_x = -1 + 2 $
$ I_x = 1A $
Questions and comments
If you have any questions, comments, etc. please post them below
- Comment 1
- Answer to Comment 1
- Comment 2
- Answer to Comment 2