| Line 1: | Line 1: | ||
| + | [[Category:ECE201]] | ||
| + | [[Category:ECE]] | ||
| + | [[Category:ECE201Spring2015Peleato]] | ||
| + | [[Category:circuits]] | ||
| + | [[Category:linear circuits]] | ||
| + | [[Category:problem solving]] | ||
| + | =Maximum Power Transferred Practice Problem= | ||
| + | <center><font size= 4> | ||
| + | '''Practice question for [[ECE201]]: "Linear circuit analysis I" ''' | ||
| + | </font size> | ||
| − | + | By: Chinar Dhamija | |
| + | Topic: Maximum Power Transferred | ||
| + | </center> | ||
| + | ---- | ||
| + | ==Question== | ||
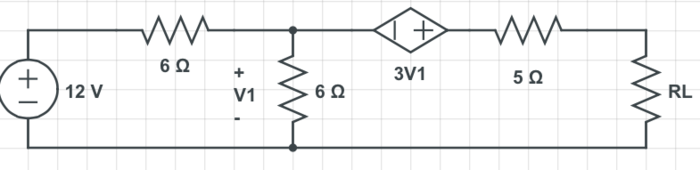
| + | What is the maximum power transferred to the load resistor. | ||
| + | [[File:ECE201_P1.png|700px|center]] | ||
| + | ---- | ||
| + | ---- | ||
| + | ===Answer === | ||
| + | Ground is located at the bottom of the circuit. | ||
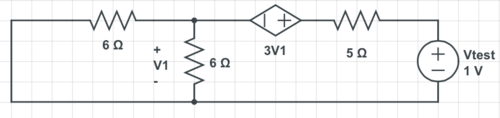
| + | First we need to find voltage and current from the perspective of the resistor load. In order to do that we need to deactivate all the independent sources and add a test source in place of RL as shown in the image below. | ||
| − | + | [[File:ECE201_P1_1.png|500px|center]] | |
| + | In this case we added a 1V test source. Since we have our Vtest we need to find Itest, which can be found by using loop analysis. | ||
| + | Let's call the 'first loop in the left box' I1 going clockwise and the 'second loop in the right box' as I2 going counterclockwise. | ||
| + | Using loop analysis we can come up with our two equations: | ||
| + | I1: 6I1 + 6(I1 + I2) = 0<br /> | ||
| + | I2: -1 + 5I2 + 3V1 + 6(I2 + I1) = 0<br /> | ||
| + | To analyze only 2 unknowns we can write V1 in terms of I1 and I2.<br /> | ||
| + | V1 = 6(I1 + I2)<br /> | ||
| + | Then substitute above equation in place of V1:<br /> | ||
| + | I1: | ||
| + | 12I1 + 6I2 = 0<br /> | ||
| + | I2 = -2I1 | ||
| + | I2: | ||
| + | -1 + 5I2 + 3(6(I1 + I2)) + 6(I2 + I1) = 0<br /> | ||
| + | -1 + 5I2 + 18I1 + 18I2 + 6I2 + 6I1 = 0<br /> | ||
| + | -1 + 29I2 + 24I1 = 0 | ||
| + | Plug I1 into the I2 equation:<br /> | ||
| + | -1 + 29(-2I1) + 24I1 = 0<br /> | ||
| + | I1 = -1/34<br /> | ||
| + | I2 = 1/17 | ||
| + | I2 = Itest = 1/17A<br /> | ||
| + | Vtest = 1V<br /> | ||
| − | [[ | + | Now we can find the equivalence resistance:<br /> |
| + | Rth = Rs = Vtest/Itest<br /> | ||
| + | = 17Ω | ||
| + | Vs = 12(6 / (6 + 6)) + 12 | ||
| + | = 18V | ||
| + | |||
| + | Pmax = Vs^2 / 4Rs | ||
| + | = 18^2 / (4 * 17) | ||
| + | '''= 4.76 W''' | ||
| + | |||
| + | ---- | ||
| + | ==Questions and comments== | ||
| + | If you have any questions, comments, etc. please post them below | ||
| + | *Comment 1 | ||
| + | **Answer to Comment 1 | ||
| + | *Comment 2 | ||
| + | **Answer to Comment 2 | ||
| + | ---- | ||
| + | [[2015 Spring ECE 201 Peleato|Back to 2015 Spring ECE 201 Peleato]] | ||
| + | |||
| + | [[ECE201|Back to ECE201]] | ||
Latest revision as of 14:01, 26 April 2015
Contents
Maximum Power Transferred Practice Problem
Practice question for ECE201: "Linear circuit analysis I"
By: Chinar Dhamija
Topic: Maximum Power Transferred
Question
What is the maximum power transferred to the load resistor.
Answer
Ground is located at the bottom of the circuit. First we need to find voltage and current from the perspective of the resistor load. In order to do that we need to deactivate all the independent sources and add a test source in place of RL as shown in the image below.
In this case we added a 1V test source. Since we have our Vtest we need to find Itest, which can be found by using loop analysis. Let's call the 'first loop in the left box' I1 going clockwise and the 'second loop in the right box' as I2 going counterclockwise. Using loop analysis we can come up with our two equations:
I1: 6I1 + 6(I1 + I2) = 0
I2: -1 + 5I2 + 3V1 + 6(I2 + I1) = 0
To analyze only 2 unknowns we can write V1 in terms of I1 and I2.
V1 = 6(I1 + I2)
Then substitute above equation in place of V1:
I1:
12I1 + 6I2 = 0
I2 = -2I1
I2:
-1 + 5I2 + 3(6(I1 + I2)) + 6(I2 + I1) = 0
-1 + 5I2 + 18I1 + 18I2 + 6I2 + 6I1 = 0
-1 + 29I2 + 24I1 = 0
Plug I1 into the I2 equation:
-1 + 29(-2I1) + 24I1 = 0
I1 = -1/34
I2 = 1/17
I2 = Itest = 1/17A
Vtest = 1V
Now we can find the equivalence resistance:
Rth = Rs = Vtest/Itest
= 17Ω
Vs = 12(6 / (6 + 6)) + 12
= 18V
Pmax = Vs^2 / 4Rs
= 18^2 / (4 * 17)
= 4.76 W
Questions and comments
If you have any questions, comments, etc. please post them below
- Comment 1
- Answer to Comment 1
- Comment 2
- Answer to Comment 2