| (2 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
---- | ---- | ||
==Question== | ==Question== | ||
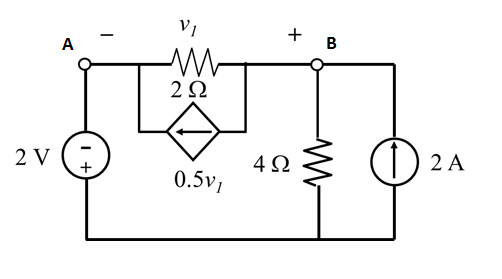
| − | The value of voltage v_1 in the following circuit is: | + | The value of voltage <math>v_1</math> in the following circuit is: |
[[File:Circuit12.png|framed|center]] | [[File:Circuit12.png|framed|center]] | ||
---- | ---- | ||
---- | ---- | ||
===Answer === | ===Answer === | ||
| − | Assuming that ground is at the bottom of the circuit, as we usually do, we want to find the voltage of the other two nodes A and B. Our unknowns will be | + | Assuming that ground is at the bottom of the circuit, as we usually do, we want to find the voltage of the other two nodes A and B. Our unknowns will be <math>V_A</math> and <math>V_B</math> and the desired voltage <math>v_1</math> can be expressed as <math>v_1=V_B-V_A</math>. |
| − | The voltage | + | The voltage <math>V_A</math> is easy to find, since node A is connected to a grounded voltage source. However, you have to be careful with the polarity of this source, since it has the plus side connected to ground and the minus side connected to the node. Then <math>V_A=-2V</math>. |
Now we need to write a nodal analysis equation to node B: | Now we need to write a nodal analysis equation to node B: | ||
| − | + | ||
| − | + | <math>\begin{align} | |
| + | \frac{V_B-V_A}{2}+0.5v_1+\frac{V_B}{4}-2= & 0\\ | ||
| + | \frac{V_B-(-2)}{2}+0.5(V_B-(-2))+\frac{V_B}{4}-2= & 0\\ | ||
| + | V_B= & 0 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Finally, <math>v_1=0-(-2)=2</math>. | ||
Latest revision as of 12:26, 18 February 2015
Problem 12 exam 1
Practice question for ECE201: "Linear circuit analysis I"
By: Anonymous
Topic: Nodal analysis
Question
The value of voltage $ v_1 $ in the following circuit is:
Answer
Assuming that ground is at the bottom of the circuit, as we usually do, we want to find the voltage of the other two nodes A and B. Our unknowns will be $ V_A $ and $ V_B $ and the desired voltage $ v_1 $ can be expressed as $ v_1=V_B-V_A $.
The voltage $ V_A $ is easy to find, since node A is connected to a grounded voltage source. However, you have to be careful with the polarity of this source, since it has the plus side connected to ground and the minus side connected to the node. Then $ V_A=-2V $.
Now we need to write a nodal analysis equation to node B:
$ \begin{align} \frac{V_B-V_A}{2}+0.5v_1+\frac{V_B}{4}-2= & 0\\ \frac{V_B-(-2)}{2}+0.5(V_B-(-2))+\frac{V_B}{4}-2= & 0\\ V_B= & 0 \end{align} $
Finally, $ v_1=0-(-2)=2 $.
Questions and comments
If you have any questions, comments, etc. please post them below
- Comment 1
- Answer to Comment 1
- Comment 2
- Answer to Comment 2