(New page: Category:ECE Category:QE Category:CNSIP Category:problem solving Category:image processing = ECE Ph.D. Qualifying Exam in Communication Ne...) |
|||
| (23 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <br> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | = [[ | + | = [[ECE PhD Qualifying Exams|ECE Ph.D. Qualifying Exam]] in Communication Networks Signal and Image processing (CS) = |
| − | = [[ECE- | + | |
| + | = [[ECE-QE CS5-2013|Question 5, August 2013]], Problem 2 = | ||
| + | |||
| + | :[[QE637 2013 Pro1|Problem 1 ]],[[QE637_2013_Pro2|Problem 2 ]] | ||
| − | |||
---- | ---- | ||
| − | |||
| + | === Solution 1: === | ||
| − | == Solution 2: == | + | a) If the color matching functions <span class="texhtml">''f''<sub>''k''</sub>(λ)</span> has negative values, it will result in negative values in <span class="texhtml">''F''<sub>''k''</sub></span>. In this case, the color can not be reproduced by this device. |
| + | |||
| + | b) The CIE color matching functions are not always positive. This is the case because, to match some reference color that is too saturated, colors have to be subtracted from the <span class="texhtml">''R'',''G'',</span> and <span class="texhtml">''B''</span> primaries. This results in negative values in tristimulus values r, g, and b. So the color matching functions at the corresponding wavelength have negative values. | ||
| + | |||
| + | c) <br> <math>\left[ {\begin{array}{*{20}{c}} | ||
| + | F_1\\ | ||
| + | F_2\\ | ||
| + | F_3 | ||
| + | \end{array}} \right] | ||
| + | = | ||
| + | {\begin{array}{*{20}{c}} | ||
| + | \int_{-\infty}^{\infty} | ||
| + | \end{array}} | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | f_1(\lambda)\\ | ||
| + | f_1(\lambda)\\ | ||
| + | f_1(\lambda) | ||
| + | \end{array}} \right] | ||
| + | I(\lambda)d\lambda | ||
| + | |||
| + | = {\begin{array}{*{20}{c}} | ||
| + | \int_{-\infty}^{\infty} | ||
| + | \end{array}} | ||
| + | M | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r_0(\lambda)\\ | ||
| + | g_0(\lambda)\\ | ||
| + | b_0(\lambda) | ||
| + | \end{array}} \right] | ||
| + | I(\lambda)d\lambda | ||
| + | |||
| + | = M | ||
| + | {\begin{array}{*{20}{c}} | ||
| + | \int_{-\infty}^{\infty} | ||
| + | \end{array}} | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r_0(\lambda)\\ | ||
| + | g_0(\lambda)\\ | ||
| + | b_0(\lambda) | ||
| + | \end{array}} \right] | ||
| + | I(\lambda)d\lambda | ||
| + | |||
| + | = M | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r\\ | ||
| + | g\\ | ||
| + | b | ||
| + | \end{array}} \right]</math> | ||
| + | |||
| + | So that, <span class="texhtml">[''r'',''g'',''b'']<sup>''t''</sup> = ''M''<sup> − 1</sup>[''F''<sub>1</sub>,''F''<sub>2</sub>,''F''<sub>3</sub>]</span>. <br> | ||
| + | |||
| + | <span style="color:green"> missed transpose sign on F. It should be <span class="texhtml">[''r'',''g'',''b'']<sup>''t''</sup> = ''M''<sup> − 1</sup>[''F''<sub>1</sub>,''F''<sub>2</sub>,''F''<sub>3</sub>]<sup>''t''</sup></span>. | ||
| + | |||
| + | |||
| + | </span> | ||
| + | <br> | ||
| + | d) It exists. CIE XYZ is one example. However, XYZ has problems with its primaries, since, the primary colors are imaginary. | ||
| + | |||
| + | == Solution 2: == | ||
| + | |||
| + | a) <span class="texhtml">''f''<sub>1</sub>(λ)</span>, <span class="texhtml">''f''<sub>2</sub>(λ)</span> and <span class="texhtml">''f''<sub>3</sub>(λ)</span> are the spectral functions for the three color outputs of color camera. It must be positive because we cannot produce negative spectrum. | ||
| + | |||
| + | b) No. <span class="texhtml">''r''<sub>''o''</sub>(λ),''g''<sub>''o''</sub>(λ)''a''''n''''d''''b'''''<b><sub>''o''</sub>(λ)</b></span>''' are CIE color matching. It takes negative value in order to substract some color to be saturated. ''' | ||
| + | |||
| + | c) | ||
| + | |||
| + | <math>\left[ {\begin{array}{*{20}{c}} | ||
| + | F_1\\ | ||
| + | F_2\\ | ||
| + | F_3 | ||
| + | \end{array}} \right] | ||
| + | = | ||
| + | {\begin{array}{*{20}{c}} | ||
| + | \int_{-\infty}^{\infty} | ||
| + | \end{array}} | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | f_1(\lambda)\\ | ||
| + | f_2(\lambda)\\ | ||
| + | f_3(\lambda) | ||
| + | \end{array}} \right] | ||
| + | I(\lambda)d\lambda | ||
| + | |||
| + | = {\begin{array}{*{20}{c}} | ||
| + | \int_{-\infty}^{\infty} | ||
| + | \end{array}} | ||
| + | M | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r_0(\lambda)\\ | ||
| + | g_0(\lambda)\\ | ||
| + | b_0(\lambda) | ||
| + | \end{array}} \right] | ||
| + | I(\lambda)d\lambda | ||
| + | |||
| + | = M | ||
| + | {\begin{array}{*{20}{c}} | ||
| + | \int_{-\infty}^{\infty} | ||
| + | \end{array}} | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r_0(\lambda)\\ | ||
| + | g_0(\lambda)\\ | ||
| + | b_0(\lambda) | ||
| + | \end{array}} \right] | ||
| + | I(\lambda)d\lambda | ||
| + | |||
| + | = M | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r\\ | ||
| + | g\\ | ||
| + | b | ||
| + | \end{array}} \right]</math> | ||
| + | |||
| + | d) | ||
| + | |||
| + | Yes. They exist. If there is a matrix M that exist to satisfy this equation <math>\left[ {\begin{array}{*{20}{c}} | ||
| + | f_1(\lambda)\\ | ||
| + | f_2(\lambda)\\ | ||
| + | f_3(\lambda) | ||
| + | \end{array}} \right] | ||
| + | = M \left[ {\begin{array}{*{20}{c}} | ||
| + | r_0(\lambda)\\ | ||
| + | g_0(\lambda)\\ | ||
| + | b_0(\lambda) | ||
| + | \end{array}} \right]</math>. | ||
| + | |||
| + | <span style="color:green"> The student can be more specific on the example of such case. I am not sure what is a good example either. Will consult Professor to figure it out.</span> | ||
---- | ---- | ||
| − | ===Related Problem=== | + | |
| + | === Related Problem === | ||
| + | |||
| + | 1. In a color matching experiment, the three primaries R, G, B are used to match the color of a pure spectral component at wavelength <span class="texhtml">λ</span>. Here the color matching allows for color to be subtracted from the reference color. At each wavelength <span class="texhtml">λ</span>, the matching color is given by | ||
| + | |||
| + | <math> | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | R, G, B | ||
| + | \end{array}} \right] | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r(\lambda)\\ | ||
| + | g(\lambda)\\ | ||
| + | b(\lambda) | ||
| + | \end{array}} \right] | ||
| + | </math> | ||
| + | |||
| + | where <span class="texhtml">''r''<sub>(</sub>λ)</span>, <span class="texhtml">''g''<sub>(</sub>λ)</span>, and <span class="texhtml">''b''<sub>(</sub>λ)</span> are normalized to 1. | ||
| + | |||
| + | Further define the white point | ||
| + | |||
| + | <math> W = | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | R, G, B | ||
| + | \end{array}} \right] | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | r_w\\ | ||
| + | g_w\\ | ||
| + | b_w | ||
| + | \end{array}} \right] | ||
| + | </math> | ||
| + | |||
| + | Let <span class="texhtml">''I''(λ)</span> be the light reflected from a surface. | ||
| + | |||
| + | a) Calculate <span class="texhtml">(''r''<sub>''e''</sub>,''g''<sub>''e''</sub>,''b''<sub>''e''</sub>)</span> the tristimulus values for the spectral distribution <span class="texhtml">''I''(λ)</span> using primaries <span class="texhtml">''R'',''G'',''B''</span> and an equal energy white point. | ||
| + | |||
| + | b) Calculate <span class="texhtml">(''r''<sub>''c''</sub>,''g''<sub>''c''</sub>,''b''<sub>''c''</sub>)</span> the tristimulus values for the spectral distribution <span class="texhtml">''I''(λ)</span> using primaries <span class="texhtml">''R'',''G'',''B''</span> and white point <span class="texhtml">(''r''<sub>''w''</sub>,''g''<sub>''w''</sub>,''b''<sub>''w''</sub>)</span>. | ||
| + | |||
| + | (Refer to ECE637 2004 Final Problem 4.) | ||
| + | |||
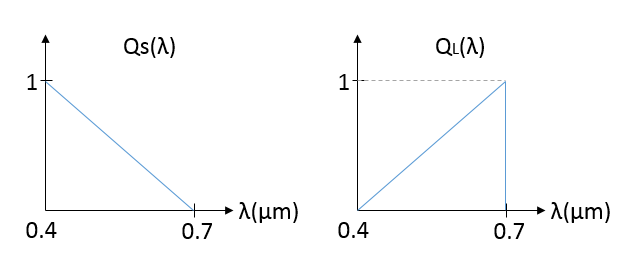
| + | 2. Consider the two channel sensors with response function <span class="texhtml">''Q''<sub>''S''</sub>(λ) ''a'''n'''d '''Q'''''<b><sub>''L''</sub>(λ). Suppose that we have two primaries <span class="texhtml">''P''<sub>''L''</sub>(λ) = σ(λ − 0.6)</span> and <span class="texhtml">''P''<sub>''S''</sub>(λ) = σ(λ − 0.5)</span>.</b></span> | ||
| + | |||
| + | <span class="texhtml">'''[[Image:QE637 2013 P2 F1.PNG]]'''</span> | ||
| + | |||
| + | Find the color matching function <math>\bar{l}(\lambda)</math> and <math>\bar{s}(\lambda)</math> for these two primaries. | ||
| + | |||
| + | (Refer to ECE638 <u>[https://engineering.purdue.edu/~ece638/lectures/03.%20Trichromatic%20theory%20-%202011.pdf Lecture note 3: Trichromatic theory of color].</u>) | ||
| + | |||
---- | ---- | ||
| − | [[ | + | |
| + | [[ECE PhD Qualifying Exams|Back to ECE QE page]]: | ||
| + | |||
| + | [[Category:ECE]] [[Category:QE]] [[Category:CNSIP]] [[Category:Problem_solving]] [[Category:Image_processing]] | ||
Latest revision as of 21:30, 2 December 2015
Contents
ECE Ph.D. Qualifying Exam in Communication Networks Signal and Image processing (CS)
Question 5, August 2013, Problem 2
- Problem 1 ,Problem 2
Solution 1:
a) If the color matching functions fk(λ) has negative values, it will result in negative values in Fk. In this case, the color can not be reproduced by this device.
b) The CIE color matching functions are not always positive. This is the case because, to match some reference color that is too saturated, colors have to be subtracted from the R,G, and B primaries. This results in negative values in tristimulus values r, g, and b. So the color matching functions at the corresponding wavelength have negative values.
c)
$ \left[ {\begin{array}{*{20}{c}} F_1\\ F_2\\ F_3 \end{array}} \right] = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} f_1(\lambda)\\ f_1(\lambda)\\ f_1(\lambda) \end{array}} \right] I(\lambda)d\lambda = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} M \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M \left[ {\begin{array}{*{20}{c}} r\\ g\\ b \end{array}} \right] $
So that, [r,g,b]t = M − 1[F1,F2,F3].
missed transpose sign on F. It should be [r,g,b]t = M − 1[F1,F2,F3]t.
d) It exists. CIE XYZ is one example. However, XYZ has problems with its primaries, since, the primary colors are imaginary.
Solution 2:
a) f1(λ), f2(λ) and f3(λ) are the spectral functions for the three color outputs of color camera. It must be positive because we cannot produce negative spectrum.
b) No. ro(λ),go(λ)a'n'd'bo(λ) are CIE color matching. It takes negative value in order to substract some color to be saturated.
c)
$ \left[ {\begin{array}{*{20}{c}} F_1\\ F_2\\ F_3 \end{array}} \right] = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} f_1(\lambda)\\ f_2(\lambda)\\ f_3(\lambda) \end{array}} \right] I(\lambda)d\lambda = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} M \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M \left[ {\begin{array}{*{20}{c}} r\\ g\\ b \end{array}} \right] $
d)
Yes. They exist. If there is a matrix M that exist to satisfy this equation $ \left[ {\begin{array}{*{20}{c}} f_1(\lambda)\\ f_2(\lambda)\\ f_3(\lambda) \end{array}} \right] = M \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] $.
The student can be more specific on the example of such case. I am not sure what is a good example either. Will consult Professor to figure it out.
Related Problem
1. In a color matching experiment, the three primaries R, G, B are used to match the color of a pure spectral component at wavelength λ. Here the color matching allows for color to be subtracted from the reference color. At each wavelength λ, the matching color is given by
$ \left[ {\begin{array}{*{20}{c}} R, G, B \end{array}} \right] \left[ {\begin{array}{*{20}{c}} r(\lambda)\\ g(\lambda)\\ b(\lambda) \end{array}} \right] $
where r(λ), g(λ), and b(λ) are normalized to 1.
Further define the white point
$ W = \left[ {\begin{array}{*{20}{c}} R, G, B \end{array}} \right] \left[ {\begin{array}{*{20}{c}} r_w\\ g_w\\ b_w \end{array}} \right] $
Let I(λ) be the light reflected from a surface.
a) Calculate (re,ge,be) the tristimulus values for the spectral distribution I(λ) using primaries R,G,B and an equal energy white point.
b) Calculate (rc,gc,bc) the tristimulus values for the spectral distribution I(λ) using primaries R,G,B and white point (rw,gw,bw).
(Refer to ECE637 2004 Final Problem 4.)
2. Consider the two channel sensors with response function QS(λ) and QL(λ). Suppose that we have two primaries PL(λ) = σ(λ − 0.6) and PS(λ) = σ(λ − 0.5).
Find the color matching function $ \bar{l}(\lambda) $ and $ \bar{s}(\lambda) $ for these two primaries.
(Refer to ECE638 Lecture note 3: Trichromatic theory of color.)