(New page: ==Periodic Signal== Let <math>x[n] = e^{jn}</math> For x[n] to be periodic, the following must hold true: <math>e^{jn} = e^{j(n+N)}</math> ==Non Periodic Signal==) |
|||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | =Periodic versus non-periodic functions ([[Homework_1_ECE301Fall2008mboutin|hw1]], [[ECE301]])= | ||
| + | <span style="color:green"> Read the instructor's comments [[hw1periodicECE301f08profcomments|here]]. </span> | ||
| + | |||
| + | A discrete time signal is periodic if there exists T > 0 such that x(t + T) = x(t) | ||
| + | |||
| + | A continuous time signal is periodic if there exists some integer N > 0 such that x[n + N] = x[n] | ||
| + | |||
==Periodic Signal== | ==Periodic Signal== | ||
| + | |||
| + | Let <math>x(t) = tan(t)</math> | ||
| + | |||
| + | For x(t) to be periodic, the following must hold true: | ||
| + | |||
| + | tan(t) = tan(t + T) for some value of T > 0 | ||
| + | |||
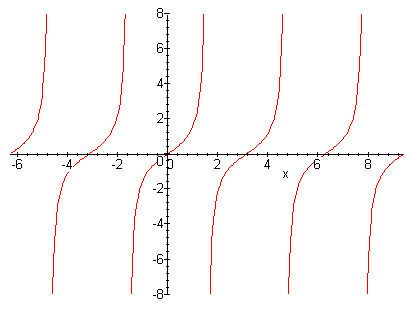
| + | Since we know that tan(t) repeats itself after every period of <math> t = \pi</math> , we know that x(t) is a periodic signal. | ||
| + | |||
| + | [[Image:Tangent_ECE301Fall2008mboutin.gif]] | ||
| + | |||
| + | ==Non Periodic Signal== | ||
Let <math>x[n] = e^{jn}</math> | Let <math>x[n] = e^{jn}</math> | ||
| Line 5: | Line 24: | ||
For x[n] to be periodic, the following must hold true: | For x[n] to be periodic, the following must hold true: | ||
| − | <math>e^{jn} = e^{j(n+N)}</math> | + | <math>e^{jn} = e^{j(n+N)}</math> for some integer N |
| − | == | + | <math>e^{jn} = e^{jn} e^{jN}</math> |
| + | |||
| + | <math>1 = e^{jN}</math> | ||
| + | |||
| + | 1 = cos(N) + jsin(N) | ||
| + | |||
| + | This equation only holds true if <math>N = 2\pi</math> or some multiple of <math>2\pi</math> | ||
| + | |||
| + | Therefore<math>x[n] = e^{jn}</math> is not periodic because <math>2\pi</math> is not an integer. | ||
Latest revision as of 06:20, 14 April 2010
Periodic versus non-periodic functions (hw1, ECE301)
Read the instructor's comments here.
A discrete time signal is periodic if there exists T > 0 such that x(t + T) = x(t)
A continuous time signal is periodic if there exists some integer N > 0 such that x[n + N] = x[n]
Periodic Signal
Let $ x(t) = tan(t) $
For x(t) to be periodic, the following must hold true:
tan(t) = tan(t + T) for some value of T > 0
Since we know that tan(t) repeats itself after every period of $ t = \pi $ , we know that x(t) is a periodic signal.
Non Periodic Signal
Let $ x[n] = e^{jn} $
For x[n] to be periodic, the following must hold true:
$ e^{jn} = e^{j(n+N)} $ for some integer N
$ e^{jn} = e^{jn} e^{jN} $
$ 1 = e^{jN} $
1 = cos(N) + jsin(N)
This equation only holds true if $ N = 2\pi $ or some multiple of $ 2\pi $
Therefore$ x[n] = e^{jn} $ is not periodic because $ 2\pi $ is not an integer.