| (20 intermediate revisions by 2 users not shown) | |||
| Line 14: | Line 14: | ||
</center> | </center> | ||
| + | ---- | ||
---- | ---- | ||
<font size = 3> | <font size = 3> | ||
| Line 53: | Line 54: | ||
Show this relationship in graph below: | Show this relationship in graph below: | ||
| − | + | ---- | |
| − | [[Image: | + | ==example== |
| + | |||
| + | [[Image:Xfcbt.png]] | ||
| + | |||
| + | [[Image:xsfcbt.png]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ==Derivation== | ||
Then we are going to find the relation between <math> X_s(f) </math> and <math> X_d(\omega) </math> | Then we are going to find the relation between <math> X_s(f) </math> and <math> X_d(\omega) </math> | ||
| Line 110: | Line 119: | ||
from this equation, we can know the relationship between <math> X_s(f) </math> and <math> X_d(\omega) </math> and the relationship is showed in graph as below: | from this equation, we can know the relationship between <math> X_s(f) </math> and <math> X_d(\omega) </math> and the relationship is showed in graph as below: | ||
| − | [[Image: | + | ---- |
| + | |||
| + | ==example== | ||
| + | |||
| + | [[Image:xsfcbt.png]] | ||
| + | |||
| + | [[Image:xdwcbt.png]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ==conclusion== | ||
| + | |||
| + | So the relationship between <math> X(f) </math> and <math> X_s(f) </math> is that <math> X_s(f) </math> is a a rep of <math> X(f) </math> in frequency domain with period of <math> \frac{1}{T} </math> and magnitude scaled by <math> \frac{1}{T} </math>. | ||
| + | the relationship between <math> X(f) </math> and <math> X_d(\omega) </math> is that <math> X_d(\omega) </math> is also a a rep of <math> X(f) </math> in frequency domain with period <math> 2\pi </math> and magnitude is also scaled by <math> \frac{1}{T} </math>, but the frequency is scaled by <math> 2\pi T </math> | ||
| + | ---- | ||
| + | |||
| + | ==Questions and Comments== | ||
| + | |||
| + | If you have any questions, comments, etc. please post them on [[frequency_domain_relation_Botao_Chen_ECE438_slecture_review|this page]]. | ||
| + | ---- | ||
| + | [[2014_Fall_ECE_438_Boutin_digital_signal_processing_slectures|Back to ECE438 slectures, Fall 2014]] | ||
Latest revision as of 18:07, 16 March 2015
Frequency domain view of the relationship between a signal and a sampling of that signal
A slecture by ECE student Botao Chen
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Contents
Outline
- Introduction
- Derivation
- Example
- Conclusion
Introduction
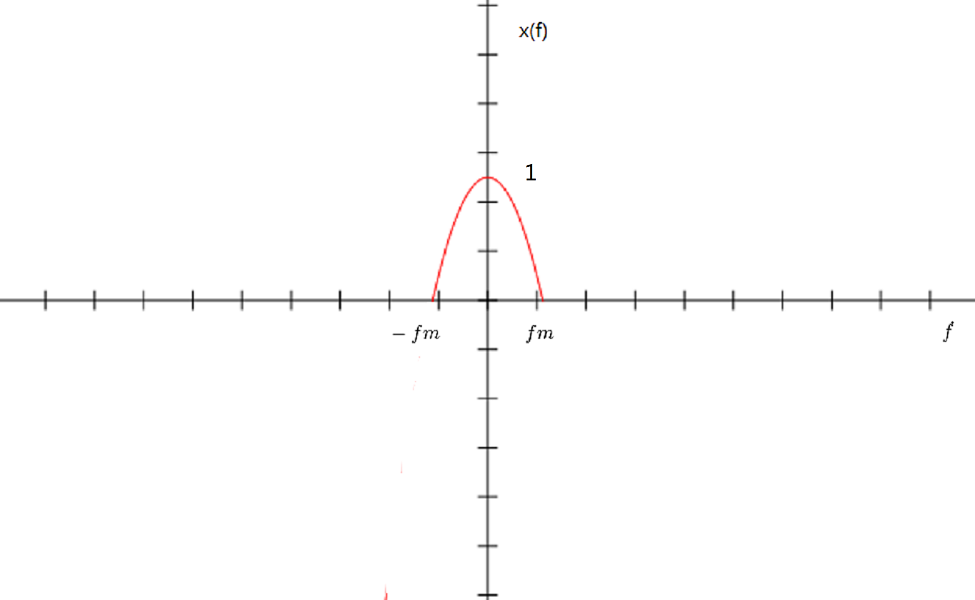
In this slecture I will discuss about the relations between the original signal $ X(f) $ (the CTFT of $ x(t) $ ), sampling continuous time signal $ X_s(f) $ (the CTFT of $ x_s(t) $ ) and sampling discrete time signal $ X_d(\omega) $ (the DTFT of $ x_d[n] $ ) in frequency domain and give a specific example showing the relations.
Derivation
The first thing which need to be clarified is that there two different types of sampling signal: $ x_s(t) $ and $ x_d[n] $. $ x_s(t) $ is created by multiplying a impulse train $ P_T(t) $ with the original signal $ x(t) $ and actually $ x_s(t) $ is $ comb_T(x(t)) $ where T is the sampling period. However the $ x_d[n] $ is $ x(nT) $ where T is the sampling period.
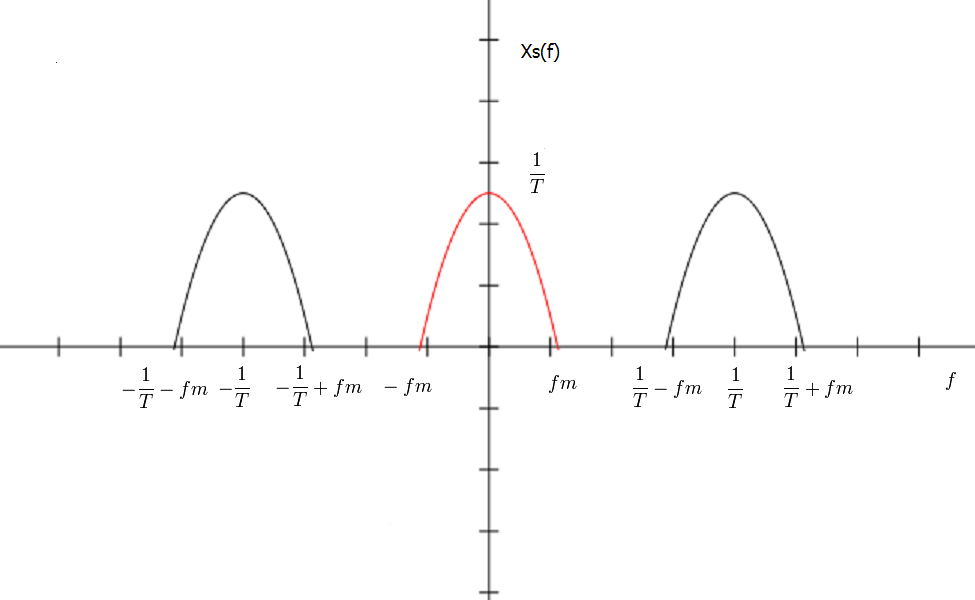
Now we first concentrate on the relationship between $ X(f) $ and $ X_s(f) $.
We know that $ x_s(t) = x(t) \times P_T(t) $, we can derive the relationship between $ x_s(t) $ and $ x(t) $ in the following way:
$ \begin{align} F(comb_T(x(t)) &= F(x(t) \times P_T(t))\\ &= X(f)*F(P_T(t))\\ &= X(f)*\frac{1}{T}\sum_{n = -\infty}^\infty \delta(f-\frac{n}{T})\\ &= \frac{1}{T}X(f)*P_\frac{1}{T}(f)\\ &= \frac{1}{T}rep_\frac{1}{T}X(f)\\ \end{align} $
Show this relationship in graph below:
example
Derivation
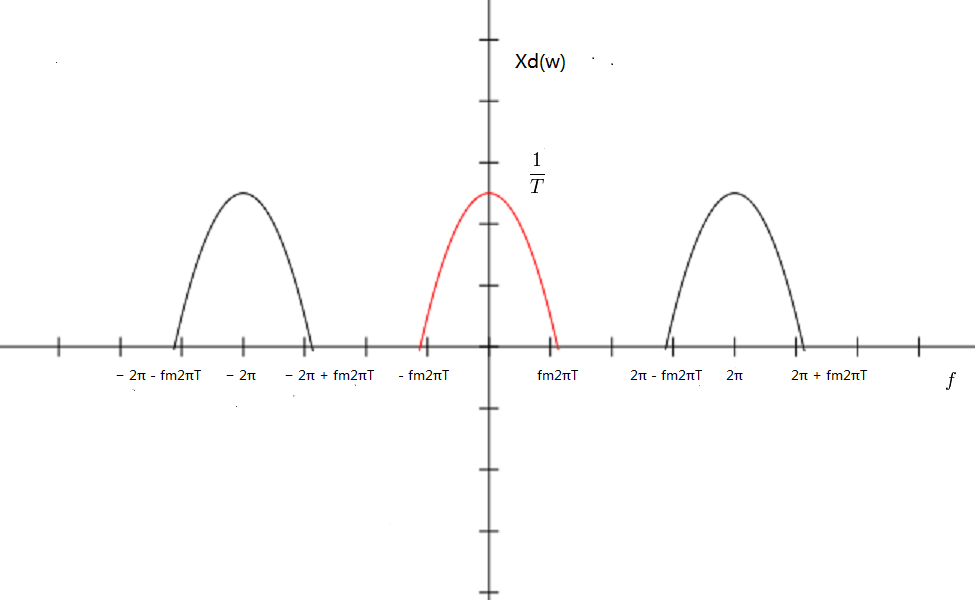
Then we are going to find the relation between $ X_s(f) $ and $ X_d(\omega) $
We know another way to express CTFT of $ x_s(t) $:
$ \begin{align} X_s(f) &= F(\sum_{n = -\infty}^\infty x(nT)\delta(t-nT))\\ &= \sum_{n = -\infty}^\infty x(nT)F(\delta(t-nT))\\ &= \sum_{n = -\infty}^\infty x(nT)e^{-j2\pi fnT}\\ \end{align} $
compare it with DTFT of $ x_d[n] $:
$ \begin{align} X_d(\omega) &= \sum_{n = -\infty}^\infty x_d[n]e^{-j\omega n}\\ &= \sum_{n = -\infty}^\infty x(nT)e^{-j\omega n}\\ \end{align} $
we can find that:
$ \begin{align} X_d(2\pi Tf) &= X_s(f)\\ \end{align} $
if $ f = \frac{1}{T} $
we have that:
$ \begin{align} X_d(2\pi ) &= X_s(\frac{1}{T})\\ \end{align} $
from this equation, we can know the relationship between $ X_s(f) $ and $ X_d(\omega) $ and the relationship is showed in graph as below:
example
conclusion
So the relationship between $ X(f) $ and $ X_s(f) $ is that $ X_s(f) $ is a a rep of $ X(f) $ in frequency domain with period of $ \frac{1}{T} $ and magnitude scaled by $ \frac{1}{T} $. the relationship between $ X(f) $ and $ X_d(\omega) $ is that $ X_d(\omega) $ is also a a rep of $ X(f) $ in frequency domain with period $ 2\pi $ and magnitude is also scaled by $ \frac{1}{T} $, but the frequency is scaled by $ 2\pi T $
Questions and Comments
If you have any questions, comments, etc. please post them on this page.