| (One intermediate revision by the same user not shown) | |||
| Line 375: | Line 375: | ||
<math>H\left( z \right) = \frac{4z^{3}\left( 1+r_1 \right) \left( 1+r_2 \right)}{z^{6}+r_1r_2z^{4}+\left(r_1+r_2 \right)z^{4} + r_1r_2z^{2} + \left(r_1+r2 \right)z^{2}+1}</math> | <math>H\left( z \right) = \frac{4z^{3}\left( 1+r_1 \right) \left( 1+r_2 \right)}{z^{6}+r_1r_2z^{4}+\left(r_1+r_2 \right)z^{4} + r_1r_2z^{2} + \left(r_1+r2 \right)z^{2}+1}</math> | ||
| + | |||
| + | (b) | ||
| + | The denominator is a polynomial with power of 6. In this case, one will get 6 roots from the equation that the polynomial equals 0. All 3 pairs of roots can be written in the format of a+(-)b*i, and b can be 0 to indicate a pair of real roots. Thus, we can find 3 formants. | ||
| + | |||
| + | (c) | ||
| + | The location of the three formants are controlled by the value of the 6 roots. The values of them vary along with the coefficients of the polynomial mentioned in part (b), while the coefficients are simply functions of <math>r_1</math> <math>r_2</math>, etc..This means that we can control the location of formants by changing the area ratio of adjacent areas. | ||
---- | ---- | ||
[[HW10ECE438F13 | Back to HW10ECE438F13 ]] | [[HW10ECE438F13 | Back to HW10ECE438F13 ]] | ||
[[2013 Fall ECE 438 Boutin|Back to 2013 Fall ECE 438 Boutin]] | [[2013 Fall ECE 438 Boutin|Back to 2013 Fall ECE 438 Boutin]] | ||
Latest revision as of 18:28, 18 November 2013
solution of Homework 10
ECE438 Fall 2013
Question 1
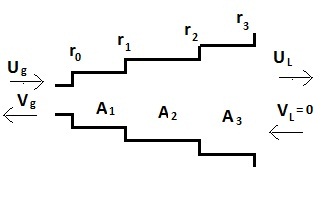
(a)
|
= | $ \begin{align} \frac{1}{1+r_0} \\\end{align} $ |
|
$ \begin{align} Z^{1/2} \\\end{align} $ |
|
$ \begin{align} \frac{1}{1+r_1} \\\end{align} $ |
|
$ \begin{align}Z^{1/2} \\\end{align} $ |
|
$ \begin{align} \frac{1}{1+r_2} \\\end{align} $ |
|
$ \begin{align}Z^{1/2} \\\end{align} $ |
|
$ \begin{align} \frac{1}{1+r_3} \\\end{align} $ |
|
|
| = | $ \begin{align} \frac{Z^{3/2}}{\pi_{k=0}^{3}(1+r_k)} \\\end{align} $ |
|
$ \begin{align} U_L \\\end{align} $ |
| = | $ \begin{align} \frac{Z^{3/2}}{\pi_{k=0}^{3}(1+r_k)} \\\end{align} $ |
|
$ \begin{align} U_L \\\end{align} $ |
| $ \begin{align} V(Z) \\\end{align} $ | = | $ \begin{align} \frac{U_L}{U_g} \\\end{align} $ | = | $ \begin{align} \frac{\pi_{k=0}^{3}(1+r_k)Z^{-3/2}}{1+(r_0r_1+r_1r_2+r_2r_3)Z^{-1}+(r_0r_1r_2r_3+r_0r_2+r_1r_3)Z^{-2}+r_0r_3Z^{-3}}\\\end{align} $ |
b) From the transfer function, we can see that there are three poles. If the poles are all real, there are three formants.
If one pole is real and the other are complex pole pair, there are two formants.
c) We can change the area of each segments. In this way,$ r_k $ will change , thus the root of the denominator of V(Z) is changed, which determines the location of formants.
Unfortunately, this solution is wrong. Can anybody post a correction below? First student who posts a correct solution will get 1% bonus. Comments and questions are welcome too. -pm
Discussion/corrections
- The expression for the transfer function is incorrect. First off, there are three tubes the air must go through, and so the top should represent a time delay by 3 time units. ($ z^{-3} $).
- Here is an easier and cleaner way to create matrices in latex. (Look at the source code of the page to copy and paste.)
- $ \left( \begin{array}{ccc} 1&2&3\\ 4&5&6\\ 7&8&9\end{array} \right) $
$ r_0=\frac{A_1-A_0}{A_1+A_0}=1 $
$ r_1=\frac{A_2-A_1}{A_2+A_1} $
$ r_2=\frac{A_3-A_2}{A_3+A_2} $
$ \left( \begin{array}{c} Ad\left(z \right) \\ Cd\left(z \right) \end{array} \right)= $$ \frac{1}{2}\left( \begin{array} {cc} 1&-1 \\ -1&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{1+r_1} \left( \begin{array}{cc} 1&-r_1 \\ -r_1&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{1+r_2} \left( \begin{array}{cc} 1&-r_2 \\ -r_2&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{2}\left( \begin{array} {cc} 1&-1 \\ -1&1 \end{array} \right) \left( \begin{array}{c} Bd\left(z \right) \\ 0 \end{array} \right) $
$ \left( \begin{array}{c} Ad\left(z \right) \\ Cd\left(z \right) \end{array} \right)= \frac{z^{3}}{4\left(1+r_1\right)\left(1+r_2\right)} \left(\begin{array} {cc} X&Y \\ Y&X \end{array} \right) \left( \begin{array}{c} Bd\left(z \right) \\ 0 \end{array} \right) $
where $ X=\frac{r_2 \left( \frac{r_1}{z^{2}}+1 \right) + \frac{r_1+\frac{1}{z^{2}}}{z^{2}}}{z^{2}} + \frac{r_1}{z^{2}} + \frac{r_2\left(r_1+\frac{1}{z^{2}} \right)}{z^{2}} + 1 $
$ Y=\frac{r_2 \left( \frac{r_1}{z^{2}}+1 \right) + \frac{r_1+\frac{1}{z^{2}}}{z^{2}}}{z^{2}} - \frac{r_1}{z^{2}} - \frac{r_2\left(r_1+\frac{1}{z^{2}} \right)}{z^{2}} - 1 $
$ H\left( z \right) = \frac{Bd\left( z \right)}{Ad \left( z \right)}=\frac{1}{X} $
Simplify X, we get
$ H\left( z \right) = \frac{4z^{3}\left( 1+r_1 \right) \left( 1+r_2 \right)}{z^{6}+r_1r_2z^{4}+\left(r_1+r_2 \right)z^{4} + r_1r_2z^{2} + \left(r_1+r2 \right)z^{2}+1} $
(b) The denominator is a polynomial with power of 6. In this case, one will get 6 roots from the equation that the polynomial equals 0. All 3 pairs of roots can be written in the format of a+(-)b*i, and b can be 0 to indicate a pair of real roots. Thus, we can find 3 formants.
(c) The location of the three formants are controlled by the value of the 6 roots. The values of them vary along with the coefficients of the polynomial mentioned in part (b), while the coefficients are simply functions of $ r_1 $ $ r_2 $, etc..This means that we can control the location of formants by changing the area ratio of adjacent areas.