| (6 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
Joseph Fourier first represented Fourier integral theorem in the following DOE: | Joseph Fourier first represented Fourier integral theorem in the following DOE: | ||
| + | <br> | ||
[[Image:DOE1.jpg]][1] | [[Image:DOE1.jpg]][1] | ||
| + | <br> | ||
Which is then introduced into the first delta function as following: | Which is then introduced into the first delta function as following: | ||
| + | <br> | ||
[[Image:DOE2.jpg]][1] | [[Image:DOE2.jpg]][1] | ||
| + | <br> | ||
And the end end up with what mathematicians called Dirac delta function: | And the end end up with what mathematicians called Dirac delta function: | ||
| + | <br> | ||
[[Image:DOE3.jpg]] [1] | [[Image:DOE3.jpg]] [1] | ||
| + | <br> | ||
| + | [1] “Dirac delta function. Internet: http://en.wikipedia.org/wiki/Dirac_delta_function, March. | ||
| + | 8, 2013 [March. 10, 2013]. | ||
[[Category:Fourier series]] | [[Category:Fourier series]] | ||
| + | <br> | ||
| + | <br> | ||
'''2.Fourier series''' | '''2.Fourier series''' | ||
| + | <br> | ||
| − | The input x(t) is a function with a fundamental period x(t)= 1 from x= 0 to 1 and f(x)= -1 to 0, with a discontinuity at x=0. | + | The input x(t) is a function with a fundamental period x(t)= 1 from x= 0 to 1 and f(x)= -1 from x= -1 to 0, with a discontinuity at x=0. |
The following graphs from matlab represents Gibbs phenomena, as n increases the overshot decreases. | The following graphs from matlab represents Gibbs phenomena, as n increases the overshot decreases. | ||
| Line 22: | Line 33: | ||
[[Image:n=100.jpg]] | [[Image:n=100.jpg]] | ||
[[Category:FFT]] | [[Category:FFT]] | ||
| + | <br> | ||
'''3.Filters''' | '''3.Filters''' | ||
| Line 27: | Line 39: | ||
[[Image:figrelena.jpg]] | [[Image:figrelena.jpg]] | ||
| + | <br> | ||
[[ECE301bonus2|Back to the 2nd bonus point opportunity, ECE301 Spring 2013]] | [[ECE301bonus2|Back to the 2nd bonus point opportunity, ECE301 Spring 2013]] | ||
Latest revision as of 10:34, 11 March 2013
1.Impulse response
Joseph Fourier first represented Fourier integral theorem in the following DOE:
![]() [1]
[1]
Which is then introduced into the first delta function as following:
![]() [1]
[1]
And the end end up with what mathematicians called Dirac delta function:
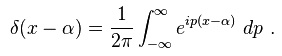 [1]
[1]
[1] “Dirac delta function. Internet: http://en.wikipedia.org/wiki/Dirac_delta_function, March.
8, 2013 [March. 10, 2013].
2.Fourier series
The input x(t) is a function with a fundamental period x(t)= 1 from x= 0 to 1 and f(x)= -1 from x= -1 to 0, with a discontinuity at x=0. The following graphs from matlab represents Gibbs phenomena, as n increases the overshot decreases.
The upper is the Gaussian filter, while bottom is the unsharp.