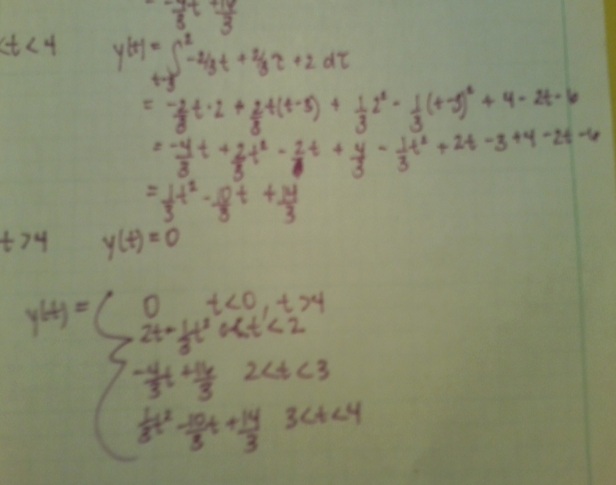Difference between revisions of "ECE301ksteckbe" - Rhea

Latest revision as of 15:48, 10 February 2013

EXTRA CREDIT

1. Linear and Non Linear

Linear example $ y[n] = 54x[n] $, $ h[n] = 62x[n] $, $ y[n] + h[n] = 54x[n] + 62x[n] $

Non Linear example $ y(t) =x^3(t) $, $ h(t) = x^3(t) $, $ y(t) + h(t) = (x(t)+x(t))^2 $ =\= $ x^2(t) +x^2(t) $

Causal and Non Causal

Causal example $ y[n]=70x[n-1] $ Non Causal example $ y[n]=76x[n+1] $

Memory and Memoryless

Memory example $ y[n]=x[n]+x[n-1] $ Memoryless example $ y[n]=36x[n] $

Invertible and noninvertible

Invertible example $ y(t)=5x(t) $ Nonivertible example $ y(t)=x^4(t) $

Stable and Nonstable

Stable example $ y(t)=sin(3t) $ Nonstable example $ y(t)=4e^3x(t) $

Time variant and Time invariant

Time variant example $ y(t)=3tx(t) $ Time Invariant example $ y(t)=3x(t) $

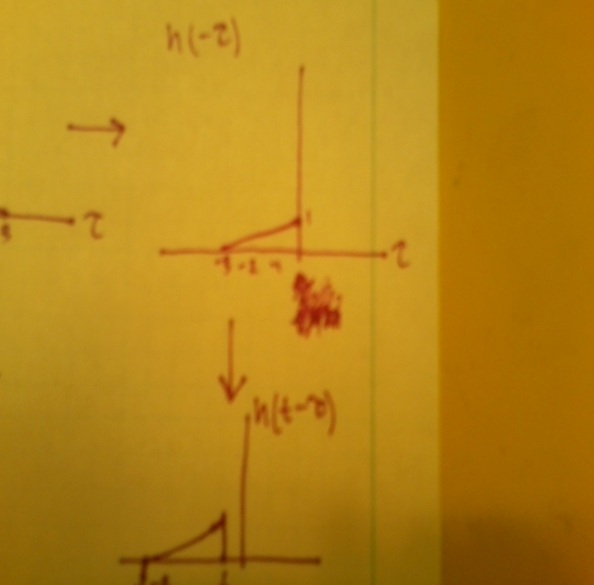
2.

Part 1:

Part 2:

Part 3:

Part 4:

I apologize for my terrible quality pictures.

3.

What is the fundamental period of the following equation.

$ y(t)=4sin(3t+pi/6) $

Its fundamental period is $ = 2pi/3 $

Comments and Questions...

Back to first bonus point opportunity, ECE301 Spring 2013