| (7 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
Therefore, if we were to randomly sample a pixel color from the image ('im1'), we would have the following probabilities of sampling each color: | Therefore, if we were to randomly sample a pixel color from the image ('im1'), we would have the following probabilities of sampling each color: | ||
| − | <math style='inline'>P( | + | <math style='inline'>P(R|im_1) = .3</math> |
| − | <math style='inline'>P( | + | <math style='inline'>P(G|im_1) = .1</math> |
| − | <math style='inline'>P( | + | <math style='inline'>P(B|im_1) = .6</math> |
Given the following probabilities of two more RGB images with the same number of pixels as im1, solve '''(a)''', '''(b)''', and '''(c)'''. (Note: we assume for this problem that pixels are sampled with replacement.) | Given the following probabilities of two more RGB images with the same number of pixels as im1, solve '''(a)''', '''(b)''', and '''(c)'''. (Note: we assume for this problem that pixels are sampled with replacement.) | ||
| − | <math style='inline'>P(R|im_1) = .3</math> <math style='inline'>P(R|im_2) = .8</math> <math style='inline'>P(R|im_3) = .4</math> | + | <math style='inline'>P(R|im_1) = .3</math> <math style='inline'>P(R|im_2) = .8</math> <math style='inline'>P(R|im_3) = .4</math> |
| − | <math style='inline'>P(G|im_1) = .1</math> <math style='inline'>P(G|im_2) = .1</math> <math style='inline'>P(G| | + | <math style='inline'>P(G|im_1) = .1</math> <math style='inline'>P(G|im_2) = .1</math> <math style='inline'>P(G|im_3) = .2</math> } where R = red pixel sampled, etc, and im1 = pixel sampled is in image 1, etc. |
| − | <math style='inline'>P(B|im_1) = .6</math> <math style='inline'>P(B|im_2) = .1</math> <math style='inline'>P(B| | + | <math style='inline'>P(B|im_1) = .6</math> <math style='inline'>P(B|im_2) = .1</math> <math style='inline'>P(B|im_3) = .4</math> |
| − | (a) Assuming that we have an equal probability of sampling a pixel from each image (ie <math style='inline'>P(im_1) = P(im_2) = P(im_3) = 1/3</math>, what is the probability that a sampled red | + | (a) Assuming that we have an equal probability of sampling a pixel from each image (ie <math style='inline'>P(im_1) = P(im_2) = P(im_3) = 1/3</math>), |
| − | + | what is the probability that a sampled red pixel came from image 3? | |
(b) Now, assume that after the first pixel is sampled, our remaining pixel samples must come from the same image as the first | (b) Now, assume that after the first pixel is sampled, our remaining pixel samples must come from the same image as the first | ||
| Line 39: | Line 39: | ||
We have been asked to find P(im3|R): | We have been asked to find P(im3|R): | ||
| − | <math style='inline'>P( | + | <math style='inline'>P(im_3|R) = \frac{P(im_3 \cap R)}{P(R)}</math> from conditional probability |
| − | <math style='inline'>= \frac{P( | + | <math style='inline'>= \frac{P(im_3)P(R|im_3)}{P(R)}</math> from Bayes' rule |
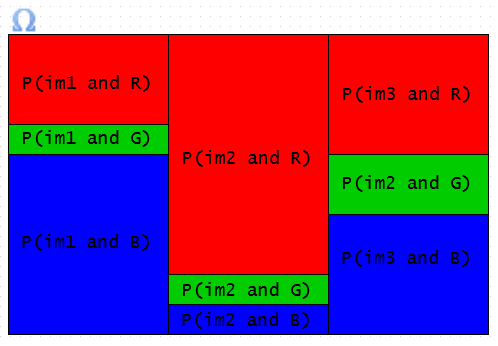
Because the numerators of the previous equation are both given, we are only left to find P(R). Since the sample space is partitioned into disjoint subsets im1, im2, and im3 (see graphic below), we can use the law of total probability: | Because the numerators of the previous equation are both given, we are only left to find P(R). Since the sample space is partitioned into disjoint subsets im1, im2, and im3 (see graphic below), we can use the law of total probability: | ||
| Line 46: | Line 46: | ||
<math>P(R) = \sum_{i=1}^{3} P(im_i)P(R|im_i) = \frac{1}{3}(.3 + .8 + .4) = .5</math> | <math>P(R) = \sum_{i=1}^{3} P(im_i)P(R|im_i) = \frac{1}{3}(.3 + .8 + .4) = .5</math> | ||
| − | <math>\therefore P( | + | <math>\therefore P(im_3|R) = \frac{(\frac{1}{3})(.4)}{.5} = \frac{.4}{1.5}</math> |
<center> | <center> | ||
| Line 53: | Line 53: | ||
'''(b)''' | '''(b)''' | ||
| − | We know that once an image has been sampled from, future | + | We know that once an image has been sampled from, future color order does not matter since pixels are sampled with replacement. However, one might think that does matter for the first pixel (when the image number is not yet known). However, after performing the following calculations, it surprisingly turns out that order does not matter for this. (I don't know why.) |
| − | + | <math>P(im_1|\{R,G,B\}) = \frac{P(im_1|R)P(\{G,B\}|im_1)}{P(\{R,G,B\})}</math> | |
| − | <math>P( | + | The calculation of <math style='inline'>P(\{R,G,B\})</math> is defined similarly to the numerator. That is: |
| − | + | <math>P(\{R,G,B\}) = \sum_{i=1}^{3} P(im_i|R)P(\{G,B\}|im_i)</math> | |
| − | <math>P( | + | Since <math style='inline'>P(\{G,B\}|im_i)</math> decomposes into <math style='inline'>P(G|im_i)P(B|im_i)</math> due to independence, the only terms we are missing are P(im1|R) and P(im2|R). However, we calculated this for image 3 in '''(a)'''. Using the same method: |
| − | + | <math>P(im1|R) = \frac{(\frac{1}{3})(.3)}{.5} = \frac{.3}{1.5}</math> | |
| − | + | ||
| + | <math>P(im2|R) = \frac{(\frac{1}{3})(.8)}{.5} = \frac{.8}{1.5}</math> | ||
| − | + | <math>\therefore P(im_1|\{R,G,B\}) = \frac{P(im_1|R)P(\{G,B\}|im_1)}{P(\{R,G,B\})} = \frac{(\frac{.3}{1.5})(.1)(.6)}{(\frac{1}{1.5})((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} = \frac{(.3)(.1)(.6)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} \approx .31</math> | |
| − | + | ||
| − | + | ||
| − | + | '''(c)''' | |
| − | + | ||
| + | Here we're looking for: | ||
| + | <math>P(R|\{R,G,B\}) = P(R|im_1)P(im_1|\{R,G,B\}) + P(R|im_2)P(im_2|\{R,G,B\}) + P(R|im_3)P(im_3|\{R,G,B\})</math> | ||
| + | <math>= \frac{(.3)(.3)(.1)(.6)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} + \frac{(.8)(.8)(.1)(.1)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} + \frac{(.4)(.4)(.2)(.4)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))}</math> | ||
| + | |||
| + | <math>\approx (.3)(.31) + (.8)(.14) + (.4)(.55) = .425</math> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ==Notes:== | ||
| + | |||
| + | If this problem is 'too long/difficult', just choose '''(a)'''. | ||
| + | |||
| + | Although I'm confident in these answers, I don't understand why order does not matter for the calculation of '''(b)'''. | ||
| + | (Perhaps my notation of the conditional probabilities is inaccurate, e.g. I'm not comfortable with events like {R,G,B}.) | ||
---- | ---- | ||
[[Bonus_point_1_ECE302_Spring2012_Boutin|Back to first bonus point opportunity, ECE302 Spring 2013]] | [[Bonus_point_1_ECE302_Spring2012_Boutin|Back to first bonus point opportunity, ECE302 Spring 2013]] | ||
Latest revision as of 18:36, 27 January 2013
Pixel = 'Pic'ture 'El'ement
Above is an RGB image with a pixel color distribution of roughly the following:
red = 30% green = 10% blue = 60%
Therefore, if we were to randomly sample a pixel color from the image ('im1'), we would have the following probabilities of sampling each color:
$ P(R|im_1) = .3 $ $ P(G|im_1) = .1 $ $ P(B|im_1) = .6 $
Given the following probabilities of two more RGB images with the same number of pixels as im1, solve (a), (b), and (c). (Note: we assume for this problem that pixels are sampled with replacement.)
$ P(R|im_1) = .3 $ $ P(R|im_2) = .8 $ $ P(R|im_3) = .4 $ $ P(G|im_1) = .1 $ $ P(G|im_2) = .1 $ $ P(G|im_3) = .2 $ } where R = red pixel sampled, etc, and im1 = pixel sampled is in image 1, etc. $ P(B|im_1) = .6 $ $ P(B|im_2) = .1 $ $ P(B|im_3) = .4 $
(a) Assuming that we have an equal probability of sampling a pixel from each image (ie $ P(im_1) = P(im_2) = P(im_3) = 1/3 $),
what is the probability that a sampled red pixel came from image 3?
(b) Now, assume that after the first pixel is sampled, our remaining pixel samples must come from the same image as the first
pixel. Given that we first sampled a red pixel, then a green and blue, what is the probability that we have been sampling
from image 1?
(c) Given the same {R,G,B} scenario as (b), and where pixels after the first must come from the same image, what is the
probability that our next (fourth) pixel sampled is red?
Solution
(a)
We have been asked to find P(im3|R):
$ P(im_3|R) = \frac{P(im_3 \cap R)}{P(R)} $ from conditional probability $ = \frac{P(im_3)P(R|im_3)}{P(R)} $ from Bayes' rule
Because the numerators of the previous equation are both given, we are only left to find P(R). Since the sample space is partitioned into disjoint subsets im1, im2, and im3 (see graphic below), we can use the law of total probability:
$ P(R) = \sum_{i=1}^{3} P(im_i)P(R|im_i) = \frac{1}{3}(.3 + .8 + .4) = .5 $
$ \therefore P(im_3|R) = \frac{(\frac{1}{3})(.4)}{.5} = \frac{.4}{1.5} $
(b)
We know that once an image has been sampled from, future color order does not matter since pixels are sampled with replacement. However, one might think that does matter for the first pixel (when the image number is not yet known). However, after performing the following calculations, it surprisingly turns out that order does not matter for this. (I don't know why.)
$ P(im_1|\{R,G,B\}) = \frac{P(im_1|R)P(\{G,B\}|im_1)}{P(\{R,G,B\})} $
The calculation of $ P(\{R,G,B\}) $ is defined similarly to the numerator. That is:
$ P(\{R,G,B\}) = \sum_{i=1}^{3} P(im_i|R)P(\{G,B\}|im_i) $
Since $ P(\{G,B\}|im_i) $ decomposes into $ P(G|im_i)P(B|im_i) $ due to independence, the only terms we are missing are P(im1|R) and P(im2|R). However, we calculated this for image 3 in (a). Using the same method:
$ P(im1|R) = \frac{(\frac{1}{3})(.3)}{.5} = \frac{.3}{1.5} $
$ P(im2|R) = \frac{(\frac{1}{3})(.8)}{.5} = \frac{.8}{1.5} $
$ \therefore P(im_1|\{R,G,B\}) = \frac{P(im_1|R)P(\{G,B\}|im_1)}{P(\{R,G,B\})} = \frac{(\frac{.3}{1.5})(.1)(.6)}{(\frac{1}{1.5})((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} = \frac{(.3)(.1)(.6)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} \approx .31 $
(c)
Here we're looking for:
$ P(R|\{R,G,B\}) = P(R|im_1)P(im_1|\{R,G,B\}) + P(R|im_2)P(im_2|\{R,G,B\}) + P(R|im_3)P(im_3|\{R,G,B\}) $
$ = \frac{(.3)(.3)(.1)(.6)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} + \frac{(.8)(.8)(.1)(.1)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} + \frac{(.4)(.4)(.2)(.4)}{((.3)(.1)(.6) + (.8)(.1)(.1) + (.4)(.2)(.4))} $
$ \approx (.3)(.31) + (.8)(.14) + (.4)(.55) = .425 $
Notes:
If this problem is 'too long/difficult', just choose (a).
Although I'm confident in these answers, I don't understand why order does not matter for the calculation of (b).
(Perhaps my notation of the conditional probabilities is inaccurate, e.g. I'm not comfortable with events like {R,G,B}.)