| (13 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[ | + | = [[:Category:Problem solving|Practice Problem on]] set operations = |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
---- | ---- | ||
| − | Consider the following sets: | + | |
| + | Consider the following sets: | ||
<math> | <math> | ||
| Line 12: | Line 10: | ||
S_2 & = \left\{ \sin (\frac{t}{2}), \sin (t+\frac{\pi}{2})\right\}. \\ | S_2 & = \left\{ \sin (\frac{t}{2}), \sin (t+\frac{\pi}{2})\right\}. \\ | ||
\end{align} | \end{align} | ||
| − | </math> | + | </math> |
| + | |||
| + | Write <math>S_1 \cup S_2</math> explicitely. Is <math>S_1 \cup S_2</math> a set? | ||
| − | |||
---- | ---- | ||
| − | ==Share your answers below== | + | |
| − | You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too! | + | == Share your answers below == |
| + | |||
| + | You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too! | ||
| + | |||
---- | ---- | ||
| − | |||
| − | + | === Answer 1 === | |
| − | + | ||
| − | + | ||
| − | ===Answer 2=== | + | No, because a set must have unique elements; sin(t+pi/2) is basically cos(t). The union of both sets is a set with elements from both S1 and S2. S1 U S2 = {sin(t),cos(t),sin(t/2)} |
| + | :<span style="color:green">Instructor's comment: Congratulations on being the first one to provide an answer. It turns out that you have made the most common mistake. But don't be ashamed: those who make the most mistakes are the ones who learn the most! Can you figure out what it is by reading the other suggested answers? -pm </span> | ||
| + | ---- | ||
| + | === Answer 2 === | ||
| − | <math | + | <math>S_1 \cup S_2 = \left\{ \sin (t),\sin (\frac{t}{2}), \cos (t)\right\}</math> |
| − | <math | + | <math>S_1 \cup S_2</math> is a set because the union of two sets is the set of all distinct elements from those two sets. In this case because <math> \sin (t+\frac{\pi}{2}) </math> and <span class="texhtml">cos(''t'')</span> are part of the same equivalence class, we only need to include one of these elements in our union set. |
| − | |||
| − | |||
---- | ---- | ||
| − | |||
| − | [[ECE302|Back to ECE302]] | + | <span style="color:green"> Instructor's suggestion: Can anyone illustrate the answer using a Venn diagram? -pm </span> |
| + | |||
| + | ---- | ||
| + | |||
| + | === Answer 3 === | ||
| + | |||
| + | S1 is sub set of S2. In venn diagram, omega which is { real positvie numbers between [-1,1]} will be entire domain. S1 will be included in S2. omega[S2[S1[]]]. I am not sure how to write mathmatical expression in this page and venn diagram. | ||
| + | |||
| + | :<span style="color:green"> YOu would have to draw the Venn diagrams using a drawing program, and then post the jpg file (or image in some other format) using the syntax <nowiki>[[Image:Example.jpg]] </nowiki>. For the math, just type the equation using the syntax <nowiki><math>Insert formula here</math></nowiki>. To use special characters in your equation, use latex code. There is a short introduction to posting equations on Rhea on [[How_to_type_Math_Equations|this page]]. -pm </span> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | <span style="color:red"> Instructor's suggestion: Everybody please comment on the above answers! You can also ask questions, or suggest alternative solutions. -pm </span> | ||
| + | |||
| + | ---- | ||
| + | === Answer 4 === | ||
| + | I guess the answer is yes, because as the result, the union set has three elements: sin(t), sin(t/2), cos(t). All the elements of the union set is distinct now, which is different from the [[Practice_Question_definition_set_ECE302S13Boutin|first practice problem]]'s case. | ||
| + | |||
| + | :<span style="color:green"> That's the idea: when one merely the lists elements of two sets, one might end up repeating elements. So taking the union of two sets is not the same as simply listing the elements of both sets in a single list. And sometimes, two elements can be expressed differently, but actually be the same exact thing! -pm </span> | ||
| + | |||
| + | ---- | ||
| + | === Answer 5 === | ||
| + | [[User:Green26|(alec green)]] | ||
| + | |||
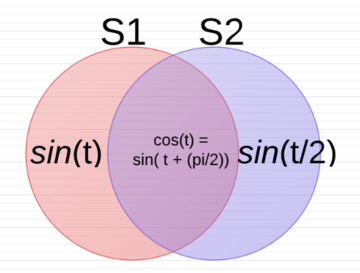
| + | [[Image:Lecture_2.PNG| 360x360px]] | ||
| + | |||
| + | So the union operator <math>\cup</math> acts as a logic OR and therefore will not doubly include redundant elements? | ||
| + | |||
| + | :<span style="color:green"> Instructor's comment: Yes, that's correct. And your picture is worth a thousand words! -pm </span> | ||
| + | ---- | ||
| + | |||
| + | [[2013 Spring ECE 302 Boutin|Back to ECE302 Spring 2013 Prof. Boutin]] | ||
| + | |||
| + | [[ECE302|Back to ECE302]] | ||
| + | |||
| + | [[Category:ECE302]] [[Category:ECE302Spring2013Boutin]] [[Category:Problem_solving]] [[Category:Set]] | ||
Latest revision as of 12:46, 13 February 2013
Contents
Practice Problem on set operations
Consider the following sets:
$ \begin{align} S_1 &= \left\{ \sin (t), \cos (t)\right\}, \\ S_2 & = \left\{ \sin (\frac{t}{2}), \sin (t+\frac{\pi}{2})\right\}. \\ \end{align} $
Write $ S_1 \cup S_2 $ explicitely. Is $ S_1 \cup S_2 $ a set?
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
No, because a set must have unique elements; sin(t+pi/2) is basically cos(t). The union of both sets is a set with elements from both S1 and S2. S1 U S2 = {sin(t),cos(t),sin(t/2)}
- Instructor's comment: Congratulations on being the first one to provide an answer. It turns out that you have made the most common mistake. But don't be ashamed: those who make the most mistakes are the ones who learn the most! Can you figure out what it is by reading the other suggested answers? -pm
Answer 2
$ S_1 \cup S_2 = \left\{ \sin (t),\sin (\frac{t}{2}), \cos (t)\right\} $
$ S_1 \cup S_2 $ is a set because the union of two sets is the set of all distinct elements from those two sets. In this case because $ \sin (t+\frac{\pi}{2}) $ and cos(t) are part of the same equivalence class, we only need to include one of these elements in our union set.
Instructor's suggestion: Can anyone illustrate the answer using a Venn diagram? -pm
Answer 3
S1 is sub set of S2. In venn diagram, omega which is { real positvie numbers between [-1,1]} will be entire domain. S1 will be included in S2. omega[S2[S1[]]]. I am not sure how to write mathmatical expression in this page and venn diagram.
- YOu would have to draw the Venn diagrams using a drawing program, and then post the jpg file (or image in some other format) using the syntax [[Image:Example.jpg]] . For the math, just type the equation using the syntax <math>Insert formula here</math>. To use special characters in your equation, use latex code. There is a short introduction to posting equations on Rhea on this page. -pm
Instructor's suggestion: Everybody please comment on the above answers! You can also ask questions, or suggest alternative solutions. -pm
Answer 4
I guess the answer is yes, because as the result, the union set has three elements: sin(t), sin(t/2), cos(t). All the elements of the union set is distinct now, which is different from the first practice problem's case.
- That's the idea: when one merely the lists elements of two sets, one might end up repeating elements. So taking the union of two sets is not the same as simply listing the elements of both sets in a single list. And sometimes, two elements can be expressed differently, but actually be the same exact thing! -pm
Answer 5
So the union operator $ \cup $ acts as a logic OR and therefore will not doubly include redundant elements?
- Instructor's comment: Yes, that's correct. And your picture is worth a thousand words! -pm