| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[Category:ECE]] | |
| + | [[Category:QE]] | ||
| + | [[Category:CNSIP]] | ||
| + | [[Category:problem solving]] | ||
| + | [[Category:image processing]] | ||
| − | = [[ECE | + | <center> |
| + | <font size= 4> | ||
| + | [[ECE_PhD_Qualifying_Exams|ECE Ph.D. Qualifying Exam]] | ||
| + | </font size> | ||
| − | + | <font size= 4> | |
| + | Communication, Networking, Signal and Image Processing (CS) | ||
| + | Question 5: Image Processing | ||
| + | </font size> | ||
| + | |||
| + | August 2011 | ||
| + | </center> | ||
| + | ---- | ||
| + | ---- | ||
| + | =Part 1 = | ||
| + | Jump to [[ECE-QE_CS5-2011_solusion-1|Part 1]],[[ECE-QE CS5-2011 solusion-2|2]] | ||
---- | ---- | ||
| Line 41: | Line 58: | ||
===== <math>\color{blue}\text{Solution 1:}</math> ===== | ===== <math>\color{blue}\text{Solution 1:}</math> ===== | ||
| + | <math>\color{green} | ||
| + | \text{Recall should be added:} | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | f(am,bn) \overset{DTFT}{\Leftrightarrow } \frac{1}{|a||b|}F(\frac{\mu}{|a|},\frac{\nu}{|b|}) | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | sinc(m,n) \overset{DTFT}{\Leftrightarrow } rect(\mu,\nu) | ||
| + | </math> | ||
<math> | <math> | ||
| Line 53: | Line 81: | ||
sinc(m,n) \rightarrow rect(\mu)rect(\nu) | sinc(m,n) \rightarrow rect(\mu)rect(\nu) | ||
</math> | </math> | ||
| + | |||
<math> | <math> | ||
| Line 58: | Line 87: | ||
</math> | </math> | ||
| − | <math> | + | |
| − | H(e^{j\mu},e^{j\nu}) | + | <font face="serif"><span style="font-size: 19px;"><math> |
| + | = H(e^{j\mu},e^{j\nu}) | ||
| + | </math></span></font> | ||
| + | |||
| + | <math>\color{green} | ||
| + | \text{Here, the student uses the Separability property of the sinc and rect functions.} | ||
</math> | </math> | ||
---- | ---- | ||
| − | <math>\color{blue}\text{b) Sketch the frequency response for } |\mu| < 2\pi \text{ and } |nu| < 2\pi \text{ when } T = \frac{1}{2} | + | <math>\color{blue}\text{b) Sketch the frequency response for } |\mu| < 2\pi \text{ and } |\nu| < 2\pi \text{ when } T = \frac{1}{2} |
</math><br> | </math><br> | ||
| + | |||
| + | <math>\color{green} | ||
| + | \text{Recall should be added:} | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | rect(t) = \left\{\begin{matrix} | ||
| + | 1, for |t|\leq \frac{1}{2} | ||
| + | \\ | ||
| + | 0, otherwise | ||
| + | \end{matrix}\right. | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>{\color{green} | ||
| + | \text{Here, the following descriptions should be clarified:} | ||
| + | }</math> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{green} | ||
| + | \text{Using the separability property for rect function, for } T = \frac{1}{2} { we have:} | ||
| + | }</math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{green} | ||
| + | H(e^{j\mu},e^{j\nu}) = \frac{1}{T^2} rect(\frac{\mu}{T},\frac{\nu}{T}) | ||
| + | }</math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{green} | ||
| + | = 4 rect(2\mu)rect(2\nu) | ||
| + | }</math></span></font> | ||
| + | |||
[[Image:QE_11_CS5_1_b.png]] | [[Image:QE_11_CS5_1_b.png]] | ||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{red} | ||
| + | \text{In this sketch it is not mentioned that the gain is } 4. | ||
| + | }</math></span></font> | ||
---- | ---- | ||
| Line 73: | Line 140: | ||
<math> | <math> | ||
| − | T = \frac{1}{2}, H(e^{j\mu},e^{j\nu}) = 4rect(2\mu)rect(\nu) | + | T = \frac{1}{2}, H(e^{j\mu},e^{j\nu}) = 4rect(2\mu)rect(2\nu) |
</math> | </math> | ||
| Line 84: | Line 151: | ||
<math>\color{blue}\text{Solution 1:}</math> | <math>\color{blue}\text{Solution 1:}</math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | \text{Recall should be added:} | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | f \left ( A \begin{bmatrix} | ||
| + | m | ||
| + | \\ | ||
| + | n | ||
| + | \end{bmatrix} \right) \overset{DTFT}{\Leftrightarrow } \frac{1}{|A|^{-1}}F([\mu, \nu] A^{-1}) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <font color="#ff0000"><span style="font-size: 17px;">'''<font face="serif"></font><math>\color{green} | ||
| + | \text{ In this case, A}= \begin{bmatrix} | ||
| + | \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ | ||
| + | -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} | ||
| + | \end{bmatrix} \text{, hence:} | ||
| + | </math>'''</span></font><font color="#ff0000"><span style="font-size: 17px;"> | ||
| + | </span></font> | ||
| Line 99: | Line 187: | ||
\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ | \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ | ||
-\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} | -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} | ||
| − | \end{bmatrix} | + | \end{bmatrix} \cdot \begin{pmatrix} |
mT\\ | mT\\ | ||
nT | nT | ||
| Line 128: | Line 216: | ||
---- | ---- | ||
| − | <math>\color{blue}\text{d) Sketch the frequency response for } |\mu| < 2\pi \text{ and } |nu| < 2\pi \text{ when } T = \frac{1}{2} | + | <math>\color{blue}\text{d) Sketch the frequency response for } |\mu| < 2\pi \text{ and } |\nu| < 2\pi \text{ when } T = \frac{1}{2} |
</math><br> | </math><br> | ||
<math>\color{blue}\text{Solution 1:}</math> | <math>\color{blue}\text{Solution 1:}</math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | \text{Recall should be added: Since A is an orthogonal matrix, this transformation is rotationally invariant.} | ||
| + | </math> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | H(e^{j\mu},e^{j\nu}) = \frac{1}{T^2} rect \left ( \frac{(\mu + \nu)}{\sqrt{2}T},\frac{(\nu - \mu)}{\sqrt{2}T} \right ) | ||
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | = 4 rect \left (\sqrt{2} (\mu + \nu),\sqrt{2}(\nu - \mu) \right ) | ||
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | \text{Or} | ||
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | = 4 rect \left (\sqrt{2} (\mu + \nu) \right) rect \left (\sqrt{2}(\nu - \mu) \right ) | ||
| + | </math></span></font> | ||
| + | |||
[[Image:QE_11_CS5_1_d.PNG]] | [[Image:QE_11_CS5_1_d.PNG]] | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{ \color{red} | ||
| + | \text{This sketch is partially correct: The cut-offs should be divided by } 4! | ||
| + | }</math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{ \color{red} | ||
| + | \text{ Also, it should be mentioned that the gain is} 4. | ||
| + | }</math></span></font> | ||
---- | ---- | ||
| Line 170: | Line 288: | ||
<math> | <math> | ||
y(m,n) = x(m,n) \cdot H(e^{j0},e^{j0}) = 4 | y(m,n) = x(m,n) \cdot H(e^{j0},e^{j0}) = 4 | ||
| + | </math> | ||
| + | |||
| + | <math>\color{red} | ||
| + | \text{The final answer is correct, but the student has skipped some parts of the derivation and the notations do not sound right.} | ||
</math> | </math> | ||
| Line 183: | Line 305: | ||
---- | ---- | ||
| − | [[ECE PhD Qualifying Exams|Back to ECE Qualifying Exams (QE) page | + | [[ECE PhD Qualifying Exams|Back to ECE Qualifying Exams (QE) page]] |
| − | + | ||
| − | + | ||
Latest revision as of 09:31, 13 September 2013
Communication, Networking, Signal and Image Processing (CS)
Question 5: Image Processing
August 2011
Part 1
Jump to Part 1,2
$ \color{blue}\text{Consider the following discrete space system with input } x(m,n) \text{ and output } y(m,n). $
$ \color{blue} y(m,n) = \sum_{k=-\infty}^{\infty}{\sum_{l=-\infty}^{\infty}{x(m-k,n-l)h(k,l)}}. $
$ \color{blue} \text{For parts a) and b) let} $
$ \color{blue} h(m,n)=sinc(mT,nT) $
$ \color{blue} \text{where } T\leq1. $
$ \color{blue} \text{For parts c), d), and e) let} $
$ \color{blue} h(m,n)=sinc\left( \frac{(n+m)T}{\sqrt[]{2}},\frac{(n-m)T}{\sqrt[]{2}} \right) $
$ \color{blue} \text{where } T\leq1. $
$ \color{blue}\text{a) Calculate the frequency response, }H \left( e^{j\mu},e^{j\nu} \right). $
$ \color{blue}\text{Solution 1:} $
$ \color{green} \text{Recall should be added:} $
$ \color{green} f(am,bn) \overset{DTFT}{\Leftrightarrow } \frac{1}{|a||b|}F(\frac{\mu}{|a|},\frac{\nu}{|b|}) $
$ \color{green} sinc(m,n) \overset{DTFT}{\Leftrightarrow } rect(\mu,\nu) $
$ H(e^{j\mu},e^{j\nu}) = \frac{1}{T^2} rect(\frac{\mu}{T},\frac{\nu}{T}) $
$ \color{blue}\text{Solution 2:} $
$ sinc(m,n) \rightarrow rect(\mu)rect(\nu) $
$ \Rightarrow sinc(mT,nT) \rightarrow \frac{1}{T^2}rect(\frac{\mu}{T})rect(\frac{\nu}{T}) $
$ = H(e^{j\mu},e^{j\nu}) $
$ \color{green} \text{Here, the student uses the Separability property of the sinc and rect functions.} $
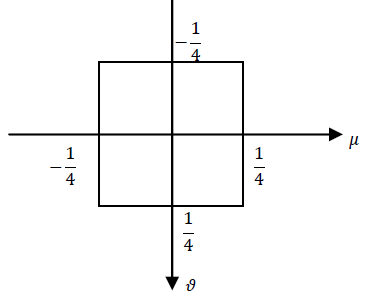
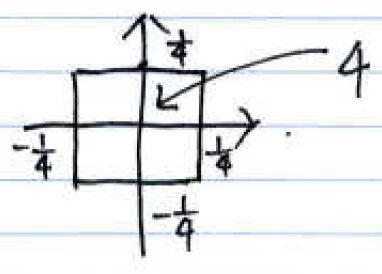
$ \color{blue}\text{b) Sketch the frequency response for } |\mu| < 2\pi \text{ and } |\nu| < 2\pi \text{ when } T = \frac{1}{2} $
$ \color{green} \text{Recall should be added:} $
$ \color{green} rect(t) = \left\{\begin{matrix} 1, for |t|\leq \frac{1}{2} \\ 0, otherwise \end{matrix}\right. $
$ {\color{green} \text{Here, the following descriptions should be clarified:} } $
$ {\color{green} \text{Using the separability property for rect function, for } T = \frac{1}{2} { we have:} } $
$ {\color{green} H(e^{j\mu},e^{j\nu}) = \frac{1}{T^2} rect(\frac{\mu}{T},\frac{\nu}{T}) } $
$ {\color{green} = 4 rect(2\mu)rect(2\nu) } $
$ {\color{red} \text{In this sketch it is not mentioned that the gain is } 4. } $
$ \color{blue}\text{Solution 2:} $
$ T = \frac{1}{2}, H(e^{j\mu},e^{j\nu}) = 4rect(2\mu)rect(2\nu) $
$ \color{blue}\text{c) Calculate the frequency response, }H \left( e^{j\mu},e^{j\nu} \right). $
$ \color{blue}\text{Solution 1:} $
$ \color{green} \text{Recall should be added:} $
$ \color{green} f \left ( A \begin{bmatrix} m \\ n \end{bmatrix} \right) \overset{DTFT}{\Leftrightarrow } \frac{1}{|A|^{-1}}F([\mu, \nu] A^{-1}) $
$ \color{green} \text{ In this case, A}= \begin{bmatrix} \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \end{bmatrix} \text{, hence:} $
$ H(e^{j\mu},e^{j\nu}) = \frac{1}{T^2} rect \left ( \frac{(\mu + \nu)}{\sqrt{2}T},\frac{(\nu - \mu)}{\sqrt{2}T} \right ) $
$ \color{blue}\text{Solution 2:} $
$ \left ( \frac{(n + m)T}{\sqrt{2}},\frac{(n - m)T}{\sqrt{2}} \right) = \begin{bmatrix} \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \end{bmatrix} \cdot \begin{pmatrix} mT\\ nT \end{pmatrix} = A \cdot \begin{pmatrix} mT\\ nT \end{pmatrix} $
$ \text{As } |A| = 1, A^{-1} = A^T, sinc \left( A \begin{pmatrix} mT\\ nT \end{pmatrix} \right) \overset{\mathcal{F}}{\rightarrow} F \left( A \begin{pmatrix} \mu\\ \nu \end{pmatrix} \right) $
$ = \frac{1}{T^2} rect \left ( \frac{(\mu + \nu)}{\sqrt{2}T},\frac{(\nu - \mu)}{\sqrt{2}T} \right ) $
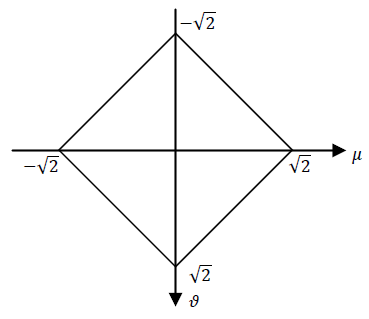
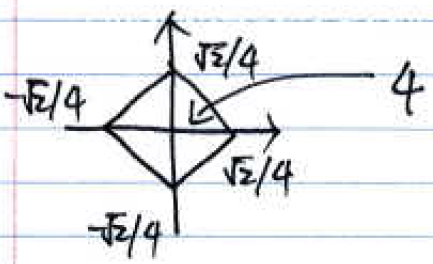
$ \color{blue}\text{d) Sketch the frequency response for } |\mu| < 2\pi \text{ and } |\nu| < 2\pi \text{ when } T = \frac{1}{2} $
$ \color{blue}\text{Solution 1:} $
$ \color{green} \text{Recall should be added: Since A is an orthogonal matrix, this transformation is rotationally invariant.} $
$ \color{green} H(e^{j\mu},e^{j\nu}) = \frac{1}{T^2} rect \left ( \frac{(\mu + \nu)}{\sqrt{2}T},\frac{(\nu - \mu)}{\sqrt{2}T} \right ) $
$ \color{green} = 4 rect \left (\sqrt{2} (\mu + \nu),\sqrt{2}(\nu - \mu) \right ) $
$ \color{green} \text{Or} $
$ \color{green} = 4 rect \left (\sqrt{2} (\mu + \nu) \right) rect \left (\sqrt{2}(\nu - \mu) \right ) $
$ { \color{red} \text{This sketch is partially correct: The cut-offs should be divided by } 4! } $
$ { \color{red} \text{ Also, it should be mentioned that the gain is} 4. } $
$ \color{blue}\text{Solution 2:} $
$ T = \frac{1}{2}, H(e^{j\mu},e^{j\nu}) = 4rect(\sqrt{2}(\mu + \nu))rect(\sqrt{2}(\nu - \mu)) $
$ \color{blue}\text{e) Calculate } y(m,n) \text{ when } x(m,n)=1. $
$ \color{blue}\text{Solution 1:} $
$ Y(e^{j\mu},e^{j\nu}) = \delta(e^{j\mu},e^{j\nu}) \cdot H(e^{j\mu},e^{j\nu}) $
$ = \frac{1}{T^2} rect (0,0) = 4 $
$ \Rightarrow y(m,n) = 4\delta(m,n) $
$ \color{blue}\text{Solution 2:} $
$ y(m,n) = x(m,n) \cdot H(e^{j0},e^{j0}) = 4 $
$ \color{red} \text{The final answer is correct, but the student has skipped some parts of the derivation and the notations do not sound right.} $
"Communication, Networks, Signal, and Image Processing" (CS)- Question 5, August 2011
Go to
- Part 1: solutions and discussions
- Part 2: solutions and discussions