| (41 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[Category:ECE]] | |
| + | [[Category:QE]] | ||
| + | [[Category:CNSIP]] | ||
| + | [[Category:problem solving]] | ||
| + | [[Category:image processing]] | ||
| − | = [[ECE | + | <center> |
| + | <font size= 4> | ||
| + | [[ECE_PhD_Qualifying_Exams|ECE Ph.D. Qualifying Exam]] | ||
| + | </font size> | ||
| − | :[[ECE-QE_CS5-2011_solusion-1|Part 1]],[[ECE-QE CS1-2011 solusion-2|2 | + | <font size= 4> |
| + | Communication, Networking, Signal and Image Processing (CS) | ||
| + | |||
| + | Question 5: Image Processing | ||
| + | </font size> | ||
| + | |||
| + | August 2011 | ||
| + | </center> | ||
| + | ---- | ||
| + | ---- | ||
| + | =Part 2= | ||
| + | Jump to [[ECE-QE_CS5-2011_solusion-1|Part 1]],[[ECE-QE CS1-2011 solusion-2|2]] | ||
---- | ---- | ||
| Line 39: | Line 57: | ||
<math> | <math> | ||
| − | + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} | |
</math> | </math> | ||
| Line 45: | Line 63: | ||
<math> | <math> | ||
= z \text{ when } \left\{\begin{matrix} | = z \text{ when } \left\{\begin{matrix} | ||
| − | r cos\theta - z sin\theta = 0 | + | r cos \theta - z sin \theta = 0 |
| − | \\ | + | \\ |
r sin \theta + z cos \theta = 0 | r sin \theta + z cos \theta = 0 | ||
\end{matrix}\right. | \end{matrix}\right. | ||
</math> | </math> | ||
| + | |||
<math> | <math> | ||
= \frac{r cos\theta}{sin \theta}, \theta > 0 | = \frac{r cos\theta}{sin \theta}, \theta > 0 | ||
| + | </math> | ||
| + | |||
| + | <math>{\color{red} | ||
| + | \text{This answer is incorrect. The correct answer is as following:}} | ||
| + | </math> | ||
| + | |||
| + | <math>{\color{green} | ||
| + | \text{Recall:}} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>{\color{green} | ||
| + | \text{i) } \int_{-\infty}^{+\infty}{f(g(t)) \delta (t) dt} = f(g(t=0)) \int_{-\infty}^{+\infty}{\delta (t) dt} | ||
| + | }</math> | ||
| + | |||
| + | |||
| + | <math>{\color{green} | ||
| + | \text{ii) } \int_{-\infty}^{+\infty}{\delta (\alpha t) dt} = \int_{-\infty}^{+\infty}{\delta (u) \frac{du}{|\alpha|}} = \frac{1}{|\alpha|} | ||
| + | }</math> | ||
| + | |||
| + | |||
| + | <math>{\color{green} | ||
| + | \text{iii) } \delta() \text{ function is separable: } \delta(x,y) = \delta(x) \cdot \delta(y) | ||
| + | }</math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | \text{ Define } u = r cos\theta - z sin\theta | ||
| + | </math></span></font> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | \Rightarrow dz = \frac{du}{|sin\theta|} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | \text{ Now } | ||
| + | </math></span></font> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(g(u)) \delta(u) \frac{du}{|sin\theta|}} = \frac{\delta(u=0)}{|sin\theta|} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | = \frac{\delta(\frac{r}{sin\theta})}{|sin\theta|} = \frac{|sin\theta|}{|sin\theta|} \delta(r) = \delta(r) | ||
</math> | </math> | ||
| Line 59: | Line 131: | ||
<math>\color{blue}\text{Solution 2:}</math> | <math>\color{blue}\text{Solution 2:}</math> | ||
| − | [[Image: | + | [[Image:.QE_11_CS5_2_a_sol2.PNG]] |
<math> | <math> | ||
| − | + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} | |
</math> | </math> | ||
| − | <math> | + | |
| − | \delta(r) | + | <font face="serif"><span style="font-size: 19px;"><math> |
| − | </math> | + | = \delta(r) |
| + | </math></span></font> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{green} | ||
| + | \text{Here, the student uses the intuitive solution: in this case the answer does not depend on } \theta \text{, since the image just contains a peak at origin. } | ||
| + | }</math></span></font> | ||
---- | ---- | ||
| Line 77: | Line 155: | ||
<math> | <math> | ||
| − | + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta - 1, r sin\theta + z cos \theta - 1) dz} | |
</math> | </math> | ||
| − | |||
<math> | <math> | ||
= z \text{ when } \left\{\begin{matrix} | = z \text{ when } \left\{\begin{matrix} | ||
| − | r cos\theta - z sin\theta = 1 | + | r cos \theta - z sin \theta = 1 |
| − | \\ | + | \\ |
r sin \theta + z cos \theta = 1 | r sin \theta + z cos \theta = 1 | ||
\end{matrix}\right. | \end{matrix}\right. | ||
</math> | </math> | ||
| + | |||
<math> | <math> | ||
| Line 93: | Line 171: | ||
</math> | </math> | ||
| + | <math>{\color{red} | ||
| + | \text{This answer is incorrect. The correct answer is as following:}} | ||
| + | </math> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | \text{ Similar to the solution 1 to part a) we define u: } u = r cos\theta - z sin\theta - 1 | ||
| + | </math></span></font> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | \text{ Following the same logic as in part a) we obtain the final answer:} | ||
| + | </math></span></font> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | p_{\theta}(r) = \delta(r - (cos\theta + sin \theta)) = \delta(r - \sqrt{2} cos (\theta - \frac{\pi}{4})) | ||
| + | </math> | ||
---- | ---- | ||
| Line 98: | Line 193: | ||
<math>\color{blue}\text{Solution 2:}</math><br> | <math>\color{blue}\text{Solution 2:}</math><br> | ||
| − | + | [[Image:QE_11_CS5_2_b_sol2.PNG]] | |
| + | |||
| + | <math> | ||
| + | \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | = \delta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{green} | ||
| + | \text{Again, the student uses the intuitive solution: in this case the answer does depend on } \theta \text{, since the peak is shifted from the origin to the point } (1,1). | ||
| + | }</math></span></font> | ||
| + | |||
---- | ---- | ||
| Line 110: | Line 225: | ||
<math> | <math> | ||
| − | + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect(\sqrt{(r cos\theta - z sin\theta)^2 + (r sin\theta + z cos \theta)^2)} dz} | |
</math> | </math> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | \text{Recall should be added:} | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | rect(t) = \left\{\begin{matrix} | ||
| + | 1, for |t|\leq \frac{1}{2} | ||
| + | \\ | ||
| + | 0, otherwise | ||
| + | \end{matrix}\right. | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} | ||
| + | \text{therefore: } | ||
| + | </math></span></font> | ||
<math> | <math> | ||
| − | = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} | + | p_{\theta}(r) = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} |
</math> | </math> | ||
| + | |||
<math> | <math> | ||
= \left\{\begin{matrix} | = \left\{\begin{matrix} | ||
| − | + | \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} | |
\\ | \\ | ||
| − | + | 0, &\text{ otherwise} | |
\end{matrix}\right. | \end{matrix}\right. | ||
</math> | </math> | ||
| − | |||
---- | ---- | ||
| Line 131: | Line 264: | ||
<math>\color{blue}\text{Solution 2:}</math><br> | <math>\color{blue}\text{Solution 2:}</math><br> | ||
| − | + | [[Image:QE_11_CS5_2_c_sol2.PNG]] | |
| + | |||
| + | <math> | ||
| + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{f(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} = \sqrt{1 - 4r^2}, \text{ if }|r| \leq \frac{1}{2} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
| + | \text{ else } p_{\theta}(r) = 0 | ||
| + | </math></span></font> | ||
| + | |||
---- | ---- | ||
| Line 141: | Line 289: | ||
<math> | <math> | ||
| − | + | p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect \left( \sqrt{(r cos\theta - z sin\theta - 1)^2 + (r sin\theta + z cos \theta - 1)^2} \right) dz} | |
</math> | </math> | ||
| Line 148: | Line 296: | ||
= \int_{-\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}^{\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}{1 dz} | = \int_{-\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}^{\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}{1 dz} | ||
</math> | </math> | ||
| + | |||
<math> | <math> | ||
= \left\{\begin{matrix} | = \left\{\begin{matrix} | ||
| − | + | \sqrt{1 - 4(r - (cos\theta + sin\theta))^2}, &\text{ if }|r| \leq \frac{1}{2} | |
\\ | \\ | ||
| − | &0, &\text{ otherwise} | + | 0, &\text{ otherwise} |
| + | \end{matrix}\right. | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>\color{green} | ||
| + | \text{ To make it more clear, the following form could be obtained:} | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
| + | = \left\{\begin{matrix} | ||
| + | \sqrt{1 - 4(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))^2}, &\text{ if }|r| \leq \frac{1}{2} | ||
| + | \\ | ||
| + | 0, &\text{ otherwise} | ||
\end{matrix}\right. | \end{matrix}\right. | ||
</math> | </math> | ||
| Line 161: | Line 323: | ||
<math>\color{blue}\text{Solution 2:}</math><br> | <math>\color{blue}\text{Solution 2:}</math><br> | ||
| − | + | <math> | |
| + | \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | \text{ where } p_\theta(r) = \left\{\begin{matrix} | ||
| + | \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} | ||
| + | \\ | ||
| + | 0, &\text{ else} | ||
| + | \end{matrix}\right. | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>{\color{green} | ||
| + | \text{Here, the student uses the results from solutions to part b and c.} | ||
| + | }</math></span></font> | ||
| + | |||
---- | ---- | ||
<math>\color{blue}\text{e) Describe in precise detail, the steps required to perform filtered back projection (FBP) reconstruction of } f(x,y). | <math>\color{blue}\text{e) Describe in precise detail, the steps required to perform filtered back projection (FBP) reconstruction of } f(x,y). | ||
| Line 169: | Line 353: | ||
<math>\color{blue}\text{Solution 1:}</math> | <math>\color{blue}\text{Solution 1:}</math> | ||
| − | <math> | + | <font face="serif"><span style="font-size: 19px;"><math> |
| − | 1. \text{ Compute } \rho_{\theta}(r) | + | 1. \text{ Compute } \rho_{\theta}(r) |
| − | </math> | + | </math></span></font> |
| − | <math> | + | |
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
2. \text{ Compute FT of step 1.} | 2. \text{ Compute FT of step 1.} | ||
| − | </math> | + | </math></span></font> |
| − | <math> | + | <font face="serif"><span style="font-size: 19px;"><math> |
| − | 3. \text{ Multiply step 2 by the filter } H(\rho) = f_c[rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c})]. | + | 3. \text{ Multiply step 2 by the filter } H(\rho) = |\rho| = f_c \left [ rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c}) \right ] |
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
| + | 4. \text{ Compute inverseFT of step 3.} | ||
| + | </math></span></font> | ||
| + | |||
| + | <math> \color{red} | ||
| + | \text{ This answer is not complete. We need the final step:} | ||
</math> | </math> | ||
| + | |||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{red} | ||
| + | 5. \text{ Back project } g_{\theta}(r) \text{ (obtained from step 4) and get: } | ||
| + | </math></span></font> | ||
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{red} | ||
| + | f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} | ||
| + | </math></span></font> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | <math>\color{blue}\text{Solution 2:}</math><br> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
| + | 1. \text{ Measure the projections } \rho_{\theta}(r) \text{ at various angles} | ||
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
| + | 2. \text{ Filter the projections } \rho_{\theta}(r) \text{ with } h(r) \text{, where } H(\rho) = |\rho| \text{ and get } g_{\theta}(r) | ||
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
| + | 3. \text{ Back project } g_{\theta}(r) \text{ along } r = xcos\theta + ysin\theta \text{ and get } | ||
| + | </math></span></font> | ||
| + | |||
| + | <font face="serif"><span style="font-size: 19px;"><math> | ||
| + | f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} | ||
| + | </math></span></font> | ||
| + | |||
| + | ---- | ||
| + | =Solution 3:= | ||
| + | |||
| + | a) | ||
| + | |||
| + | <math>p_\theta(r)=\begin{cases}1, & \text{if } r=0\\0, & \text{otherwisr}\end{cases}=\delta(r)</math>. | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_a_sol3.png|200px]] | ||
| + | |||
| + | |||
| + | b) | ||
| + | |||
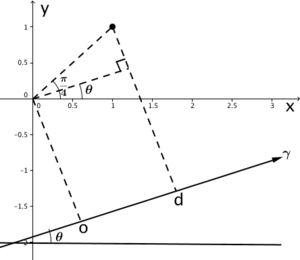
| + | * If <math>0\leq\theta<\frac{\pi}{4}</math>, <math>d=\sqrt{2}\text{cos}(\frac{\pi}{4}-\theta)=\sqrt{2}[\text{cos}\frac{\pi}{4}\text{cos}\theta+\text{sin}\frac{\pi}{4}\text{sin}\theta]=\text{cos}\theta+\text{sin}\theta</math>. | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_b_1_sol3.png|300px]] | ||
| + | |||
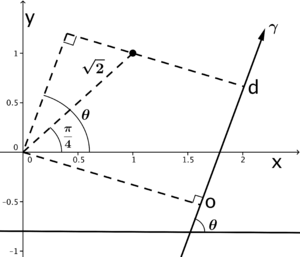
| + | * If <math>\frac{\pi}{4}\leq \theta < \frac{\pi}{2}</math>, <math>d=\sqrt{2}\text{cos}(\theta-\frac{\pi}{4})=\sqrt{2}\text{cos}(\frac{\pi}{4}-\theta)=\text{cos}\theta+\text{sin}\theta</math>. | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_b_2_sol3.png|300px]] | ||
| + | |||
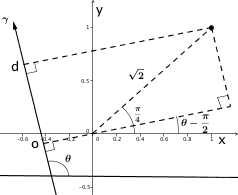
| + | * If <math>\frac{\pi}{2}\leq \theta < \frac{3\pi}{4}</math>, <math>d=\sqrt{2}\text{sin}(\frac{\pi}{4}-(\theta-\frac{\pi}{2}))=\sqrt{2}\text{sin}(\frac{3\pi}{4}-\theta)=\sqrt{2}[\text{sin}\frac{3\pi}{4}\text{cos}\theta-\text{cos}\frac{3\pi}{4}\text{sin}\theta]=\text{cos}\theta+\text{sin}\theta</math>. | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_b_3_sol3.png|300px]] | ||
| + | |||
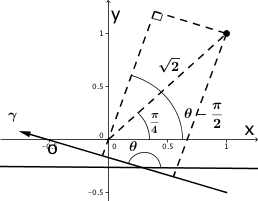
| + | * If <math>\frac{3\pi}{4}\leq \theta < 2\pi</math>, <math>d=-\sqrt{2}\text{sin}(\theta-\frac{\pi}{2}-\frac{\pi}{4})=-\sqrt{2}\text{sin}(\theta-\frac{3\pi}{4})=-\sqrt{2}[\text{sin}\theta\text{cos}\frac{3\pi}{4}-\text{cos}\theta\text{sin}\frac{3\pi}{4}]=\text{cos}\theta+\text{sin}\theta</math>. | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_b_4_sol3.png|300px]] | ||
| + | |||
| + | <math>\Rightarrow p_\theta(r)=\delta(r-(\text{cos}\theta+\text{sin}\theta))</math> for all <math>\theta</math>. | ||
| + | |||
| + | |||
| + | c) | ||
| + | |||
| + | Since <math>f(x,y)</math> is symmetric to <math>(0,0)</math> | ||
| + | |||
| + | <math>\Rightarrow p_\theta(r)=p_0(r)=\int_{-\sqrt{\frac{1}{4}-r^2}}^{\sqrt{\frac{1}{4}-r^2}}1\cdot dz=2\int_0^{\sqrt{\frac{1}{4}-r^2}}1\cdot dz\text{, for }\vert r\vert<\frac{1}{2}</math> | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_c_sol3.png|200px]] | ||
| + | |||
| + | <math>\Rightarrow p_\theta(r)=2\sqrt{\frac{1}{4}-r^2}\text{rect}(r)</math> | ||
| + | |||
| + | |||
| + | d) | ||
| + | |||
| + | From part (b), we know that, if <math>f(x,y)</math> has <math>(1,1)</math> shift in <math>x-y</math> plane, the <math>p_\theta(r)</math> would have <math>(\text{cos}\theta+\text{sin}\theta)</math> shift in <math>r</math>-direction. | ||
| + | |||
| + | <math>\Rightarrow p_\theta(r)=2\sqrt{\frac{1}{4}-(r-(\text{cos}\theta+\text{sin}\theta))^2}\text{rect}(r-(\text{cos}\theta+\text{sin}\theta))</math> | ||
| + | |||
| + | |||
| + | e) | ||
| + | |||
| + | * First, measure the forward projection <math>p_\theta(r)</math> for sufficient angles <math>\theta s</math>. | ||
| + | * Second, filter the forward projection with <math>h(r): g_\theta(r)=h(r)\ast p_\theta(r)</math>, where <math>h(r)=\text{CTFT}^{-1}\left\{\vert\rho\vert\right\}</math>. | ||
| + | * Finally, back project filtered projection to reconstruct <math>f(x,y)</math>. <math>f(x,y)=\int_0^\pi g_\theta(x\text{cos}\theta+y\text{sin}\theta)d\theta</math>. | ||
| + | |||
| + | |||
| + | |||
| + | =Solution 4:= | ||
| + | |||
| + | a) | ||
| + | |||
| + | <math>P_\theta(\rho)=F(\rho\text{cos}\theta, \rho\text{sin}\theta)</math> | ||
| + | |||
| + | When <math>f(x,y)=\delta(x,y)</math>, <math>F(\mu,\nu)=1</math>. | ||
| + | |||
| + | So <math>p_\theta(r)=\delta_\theta(r)</math>. | ||
| + | |||
| + | <font color="green"><u>'''Comments'''</u>: | ||
| + | |||
| + | * The answer would be easier to understand if the last statement was expressed in this way: <math>p_{\theta}(r)=\mathcal{F}^{-1}\{ P_{\theta}(\rho)\}=\mathcal{F}^{-1}\{1\}=\delta_{\theta}(r)</math>, where <math>\mathcal{F}^{-1}\{\cdot\}</math> is the Fourier inverse transform. | ||
| + | |||
| + | </font> | ||
| + | |||
| + | |||
| + | b) | ||
| + | |||
| + | When <math>f(x,y)=\delta(x-1,y-1)</math>, <math>F(\mu,\nu)=e^{-j\mu}\cdot e^{-j\nu}</math>. | ||
| + | |||
| + | So <math>P_\theta(\rho)=e^{-j\rho\text{cos}\theta}\cdot e^{-j\rho\text{sin}\theta}</math>, <math>p_\theta(r)=\delta(r-\text{cos}\theta-\text{sin}\theta)</math>. | ||
| + | |||
| + | |||
| + | c) | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_c_sol4.png|200px]] | ||
| + | |||
| + | <math>p_\theta(r)=\int_{-\sqrt{\frac{1}{4}-r^2}}^{\sqrt{\frac{1}{4}-r^2}}1dz=\sqrt{1-4r^2}</math> | ||
| + | |||
| + | So <math>p_\theta(r)=\begin{cases} \sqrt{1-4r^2}, & |r|<\frac{1}{2}\\0, & |r|>\frac{1}{2}\end{cases}</math>. | ||
| + | |||
| + | |||
| + | d) | ||
| + | |||
| + | [[Image:CW_QE_2011_CS5_2_d_sol4.png|300px]] | ||
| + | |||
| + | <math>r_0=\sqrt{2}\cdot\left(\frac{\pi}{4}-\theta\right)</math> | ||
| + | |||
| + | <math>p_\theta(r)=\int_{-\infty}^{\infty}f(r\text{cos}\theta-z\text{sin}\theta, r\text{sin}\theta+z\text{cos}\theta)dz=\int_{-\sqrt{\frac{1}{4}-(r-r_0)^2}}^{\sqrt{\frac{1}{4}-(r-r_0)^2}}adz</math> | ||
| + | |||
| + | So <math>p_\theta(r)=\begin{cases}\sqrt{1-4\left(r-\sqrt{2}\left(\frac{\pi}{4}-\theta\right)\right)}, & |r-r_0|\leq\frac{1}{2}\\0, & \text{otherwise}\end{cases}</math>. | ||
| + | |||
| + | <font color="green"><u>'''Comments'''</u>: | ||
| + | |||
| + | * The computation for <math>r_0</math> is wrong. The correct expression of <math>r_0</math> should be: <math>r_0 = \sqrt{2}\sin(\frac{\pi}{4}-\theta)</math>. It can also be expressed as: <math>r_0=\cos\theta+\sin\theta</math>. | ||
| + | * The rest statement is correct, and then the final result becomes: <math>p_{\theta}(r)=\begin{cases}\sqrt{1-4(r-r_0)}, & |r-r_0|\leq\frac{1}{2}\\0, & \text{otherwise} \end{cases}</math>. | ||
| + | |||
| + | </font> | ||
| + | |||
| + | |||
| + | e) | ||
| + | |||
<math> | <math> | ||
| − | + | \begin{align} | |
| + | f(x,y) & =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(\mu,\nu)e^{2\pi j(x\mu+y\nu)}d\mu d\nu\\ | ||
| + | & = \int_{-\infty}^{\infty}\int_{0}^{\pi}p_\theta(\rho)e^{2\pi j(x\rho\text{cos}\theta+y\rho\text{sin}\theta)}|\rho|d\theta d\rho\\ | ||
| + | & = \int_{0}^{\pi}\underbrace{\int_{-\infty}^{\infty}|\rho|p_\theta(\rho)e^{2\pi j(x\rho\text{cos}\theta+y\rho\text{sin}\theta)}d\rho}_{g_\theta(x\text{cos}\theta+y\text{sin}\theta)}d\theta | ||
| + | \end{align} | ||
</math> | </math> | ||
| + | |||
| + | So <math>g_\theta(t)</math> is given by: | ||
| + | |||
| + | <math>g_\theta(t)=\int_{-\infty}^{\infty}|\rho|p_\theta(\rho)e^{2\pi j\rho t}d\rho=\text{CTFT}^{-1}\{|\rho|p_\theta(\rho)\}=h(t)\ast p_\theta(r)</math> | ||
| + | |||
| + | So what we do is: | ||
| + | |||
| + | # measure projection <math>p_\theta(r)</math>; | ||
| + | # filter the projection <math>g_\theta(r)=h(r)\ast p_\theta(r)</math>; | ||
| + | # back project filtered projection: <math>f(x,y)=\int_0^{\pi}g_\theta(x\text{cos}\theta)+y\text{sin}\theta)d\theta</math>. | ||
---- | ---- | ||
| + | =Related Problems= | ||
| − | <math>\ | + | a) Calculate the forward projection <math>p_\theta(r)</math>, for <math>f(x,y)=\text{rect}(x,y)</math>, as <math>\theta=0</math> and <math>\theta=\pi/4</math>. |
| + | |||
| + | b) Calculate the forward projection <math>p_\theta(r)</math>, for <math>f(x,y)=\delta(x-a,y-b)</math>. | ||
| − | |||
---- | ---- | ||
| Line 202: | Line 550: | ||
---- | ---- | ||
| − | [[ECE PhD Qualifying Exams|Back to ECE Qualifying Exams (QE) page | + | [[ECE PhD Qualifying Exams|Back to ECE Qualifying Exams (QE) page]] |
| − | + | ||
| − | + | ||
Latest revision as of 00:51, 31 March 2015
Communication, Networking, Signal and Image Processing (CS)
Question 5: Image Processing
August 2011
Contents
Part 2
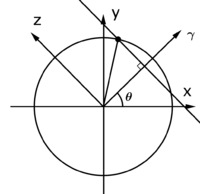
$ \color{blue}\text{Consider an image } f(x,y) \text{ with a forward projection} $
$ \color{blue} p_{\theta}(r) = \mathcal{FP}\left \{ f(x,y) \right \} $
$ \color{blue} = \int_{-\infty}^{\infty}{f \left ( r cos(\theta) - z sin(\theta),r sin(\theta) + z cos(\theta) \right )dz}. $
$ \color{blue} \text{Let } F(\mu,\nu) \text{ be the continuous-time Fourier transform of } f(x,y) \text{ given by} $
$ \color{blue} F(u,v) = \int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(x,y)e^{-j2\pi(ux,vy)}dx}dy} $
$ \color{blue} \text{and let } P_{\theta}(\rho) \text{ be the continuous-time Fourier transform of } p_{\theta}(r) \text{ given by} $
$ \color{blue} P_{\theta}(\rho) = \int_{-\infty}^{\infty}{p_{\theta}(r)e^{-j2\pi(\rho r)}dr}. $
$ \color{blue}\text{a) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = \delta(x,y). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ = z \text{ when } \left\{\begin{matrix} r cos \theta - z sin \theta = 0 \\ r sin \theta + z cos \theta = 0 \end{matrix}\right. $
$ = \frac{r cos\theta}{sin \theta}, \theta > 0 $
$ {\color{red} \text{This answer is incorrect. The correct answer is as following:}} $
$ {\color{green} \text{Recall:}} $
$ {\color{green} \text{i) } \int_{-\infty}^{+\infty}{f(g(t)) \delta (t) dt} = f(g(t=0)) \int_{-\infty}^{+\infty}{\delta (t) dt} } $
$ {\color{green} \text{ii) } \int_{-\infty}^{+\infty}{\delta (\alpha t) dt} = \int_{-\infty}^{+\infty}{\delta (u) \frac{du}{|\alpha|}} = \frac{1}{|\alpha|} } $
$ {\color{green} \text{iii) } \delta() \text{ function is separable: } \delta(x,y) = \delta(x) \cdot \delta(y) } $
$ \color{green} \text{ Define } u = r cos\theta - z sin\theta $
$ \color{green} \Rightarrow dz = \frac{du}{|sin\theta|} $
$ \color{green} \text{ Now } $
$ \color{green} p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ \color{green} p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(g(u)) \delta(u) \frac{du}{|sin\theta|}} = \frac{\delta(u=0)}{|sin\theta|} $
$ \color{green} = \frac{\delta(\frac{r}{sin\theta})}{|sin\theta|} = \frac{|sin\theta|}{|sin\theta|} \delta(r) = \delta(r) $
$ \color{blue}\text{Solution 2:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ = \delta(r) $
$ {\color{green} \text{Here, the student uses the intuitive solution: in this case the answer does not depend on } \theta \text{, since the image just contains a peak at origin. } } $
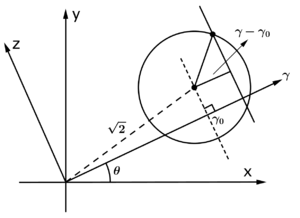
$ \color{blue}\text{b) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = \delta(x-1,y-1). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta - 1, r sin\theta + z cos \theta - 1) dz} $
$ = z \text{ when } \left\{\begin{matrix} r cos \theta - z sin \theta = 1 \\ r sin \theta + z cos \theta = 1 \end{matrix}\right. $
$ = \frac{r cos\theta - 1}{sin \theta}, \theta > 0 $
$ {\color{red} \text{This answer is incorrect. The correct answer is as following:}} $
$ \color{green} \text{ Similar to the solution 1 to part a) we define u: } u = r cos\theta - z sin\theta - 1 $
$ \color{green} \text{ Following the same logic as in part a) we obtain the final answer:} $
$ \color{green} p_{\theta}(r) = \delta(r - (cos\theta + sin \theta)) = \delta(r - \sqrt{2} cos (\theta - \frac{\pi}{4})) $
$ \color{blue}\text{Solution 2:} $
$ \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) $
$ = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $
$ = \delta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $
$ {\color{green} \text{Again, the student uses the intuitive solution: in this case the answer does depend on } \theta \text{, since the peak is shifted from the origin to the point } (1,1). } $
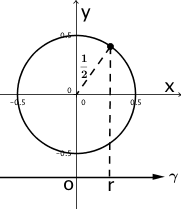
$ \color{blue}\text{c) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = rect \left(\sqrt[]{x^2+y^2} \right). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect(\sqrt{(r cos\theta - z sin\theta)^2 + (r sin\theta + z cos \theta)^2)} dz} $
$ \color{green} \text{Recall should be added:} $
$ \color{green} rect(t) = \left\{\begin{matrix} 1, for |t|\leq \frac{1}{2} \\ 0, otherwise \end{matrix}\right. $
$ \color{green} \text{therefore: } $
$ p_{\theta}(r) = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} $
$ = \left\{\begin{matrix} \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $
$ \color{blue}\text{Solution 2:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{f(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} = \sqrt{1 - 4r^2}, \text{ if }|r| \leq \frac{1}{2} $
$ \text{ else } p_{\theta}(r) = 0 $
$ \color{blue}\text{d) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = rect \left(\sqrt[]{(x-1)^2+(y-1)^2} \right). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect \left( \sqrt{(r cos\theta - z sin\theta - 1)^2 + (r sin\theta + z cos \theta - 1)^2} \right) dz} $
$ = \int_{-\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}^{\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}{1 dz} $
$ = \left\{\begin{matrix} \sqrt{1 - 4(r - (cos\theta + sin\theta))^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $
$ \color{green} \text{ To make it more clear, the following form could be obtained:} $
$ \color{green} = \left\{\begin{matrix} \sqrt{1 - 4(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $
$ \color{blue}\text{Solution 2:} $
$ \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) $
$ = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $
$ \text{ where } p_\theta(r) = \left\{\begin{matrix} \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ else} \end{matrix}\right. $
$ {\color{green} \text{Here, the student uses the results from solutions to part b and c.} } $
$ \color{blue}\text{e) Describe in precise detail, the steps required to perform filtered back projection (FBP) reconstruction of } f(x,y). $
$ \color{blue}\text{Solution 1:} $
$ 1. \text{ Compute } \rho_{\theta}(r) $
$ 2. \text{ Compute FT of step 1.} $
$ 3. \text{ Multiply step 2 by the filter } H(\rho) = |\rho| = f_c \left [ rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c}) \right ] $
$ 4. \text{ Compute inverseFT of step 3.} $
$ \color{red} \text{ This answer is not complete. We need the final step:} $
$ \color{red} 5. \text{ Back project } g_{\theta}(r) \text{ (obtained from step 4) and get: } $
$ \color{red} f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} $
$ \color{blue}\text{Solution 2:} $
$ 1. \text{ Measure the projections } \rho_{\theta}(r) \text{ at various angles} $
$ 2. \text{ Filter the projections } \rho_{\theta}(r) \text{ with } h(r) \text{, where } H(\rho) = |\rho| \text{ and get } g_{\theta}(r) $
$ 3. \text{ Back project } g_{\theta}(r) \text{ along } r = xcos\theta + ysin\theta \text{ and get } $
$ f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} $
Solution 3:
a)
$ p_\theta(r)=\begin{cases}1, & \text{if } r=0\\0, & \text{otherwisr}\end{cases}=\delta(r) $.
b)
- If $ 0\leq\theta<\frac{\pi}{4} $, $ d=\sqrt{2}\text{cos}(\frac{\pi}{4}-\theta)=\sqrt{2}[\text{cos}\frac{\pi}{4}\text{cos}\theta+\text{sin}\frac{\pi}{4}\text{sin}\theta]=\text{cos}\theta+\text{sin}\theta $.
- If $ \frac{\pi}{4}\leq \theta < \frac{\pi}{2} $, $ d=\sqrt{2}\text{cos}(\theta-\frac{\pi}{4})=\sqrt{2}\text{cos}(\frac{\pi}{4}-\theta)=\text{cos}\theta+\text{sin}\theta $.
- If $ \frac{\pi}{2}\leq \theta < \frac{3\pi}{4} $, $ d=\sqrt{2}\text{sin}(\frac{\pi}{4}-(\theta-\frac{\pi}{2}))=\sqrt{2}\text{sin}(\frac{3\pi}{4}-\theta)=\sqrt{2}[\text{sin}\frac{3\pi}{4}\text{cos}\theta-\text{cos}\frac{3\pi}{4}\text{sin}\theta]=\text{cos}\theta+\text{sin}\theta $.
- If $ \frac{3\pi}{4}\leq \theta < 2\pi $, $ d=-\sqrt{2}\text{sin}(\theta-\frac{\pi}{2}-\frac{\pi}{4})=-\sqrt{2}\text{sin}(\theta-\frac{3\pi}{4})=-\sqrt{2}[\text{sin}\theta\text{cos}\frac{3\pi}{4}-\text{cos}\theta\text{sin}\frac{3\pi}{4}]=\text{cos}\theta+\text{sin}\theta $.
$ \Rightarrow p_\theta(r)=\delta(r-(\text{cos}\theta+\text{sin}\theta)) $ for all $ \theta $.
c)
Since $ f(x,y) $ is symmetric to $ (0,0) $
$ \Rightarrow p_\theta(r)=p_0(r)=\int_{-\sqrt{\frac{1}{4}-r^2}}^{\sqrt{\frac{1}{4}-r^2}}1\cdot dz=2\int_0^{\sqrt{\frac{1}{4}-r^2}}1\cdot dz\text{, for }\vert r\vert<\frac{1}{2} $
$ \Rightarrow p_\theta(r)=2\sqrt{\frac{1}{4}-r^2}\text{rect}(r) $
d)
From part (b), we know that, if $ f(x,y) $ has $ (1,1) $ shift in $ x-y $ plane, the $ p_\theta(r) $ would have $ (\text{cos}\theta+\text{sin}\theta) $ shift in $ r $-direction.
$ \Rightarrow p_\theta(r)=2\sqrt{\frac{1}{4}-(r-(\text{cos}\theta+\text{sin}\theta))^2}\text{rect}(r-(\text{cos}\theta+\text{sin}\theta)) $
e)
- First, measure the forward projection $ p_\theta(r) $ for sufficient angles $ \theta s $.
- Second, filter the forward projection with $ h(r): g_\theta(r)=h(r)\ast p_\theta(r) $, where $ h(r)=\text{CTFT}^{-1}\left\{\vert\rho\vert\right\} $.
- Finally, back project filtered projection to reconstruct $ f(x,y) $. $ f(x,y)=\int_0^\pi g_\theta(x\text{cos}\theta+y\text{sin}\theta)d\theta $.
Solution 4:
a)
$ P_\theta(\rho)=F(\rho\text{cos}\theta, \rho\text{sin}\theta) $
When $ f(x,y)=\delta(x,y) $, $ F(\mu,\nu)=1 $.
So $ p_\theta(r)=\delta_\theta(r) $.
Comments:
- The answer would be easier to understand if the last statement was expressed in this way: $ p_{\theta}(r)=\mathcal{F}^{-1}\{ P_{\theta}(\rho)\}=\mathcal{F}^{-1}\{1\}=\delta_{\theta}(r) $, where $ \mathcal{F}^{-1}\{\cdot\} $ is the Fourier inverse transform.
b)
When $ f(x,y)=\delta(x-1,y-1) $, $ F(\mu,\nu)=e^{-j\mu}\cdot e^{-j\nu} $.
So $ P_\theta(\rho)=e^{-j\rho\text{cos}\theta}\cdot e^{-j\rho\text{sin}\theta} $, $ p_\theta(r)=\delta(r-\text{cos}\theta-\text{sin}\theta) $.
c)
$ p_\theta(r)=\int_{-\sqrt{\frac{1}{4}-r^2}}^{\sqrt{\frac{1}{4}-r^2}}1dz=\sqrt{1-4r^2} $
So $ p_\theta(r)=\begin{cases} \sqrt{1-4r^2}, & |r|<\frac{1}{2}\\0, & |r|>\frac{1}{2}\end{cases} $.
d)
$ r_0=\sqrt{2}\cdot\left(\frac{\pi}{4}-\theta\right) $
$ p_\theta(r)=\int_{-\infty}^{\infty}f(r\text{cos}\theta-z\text{sin}\theta, r\text{sin}\theta+z\text{cos}\theta)dz=\int_{-\sqrt{\frac{1}{4}-(r-r_0)^2}}^{\sqrt{\frac{1}{4}-(r-r_0)^2}}adz $
So $ p_\theta(r)=\begin{cases}\sqrt{1-4\left(r-\sqrt{2}\left(\frac{\pi}{4}-\theta\right)\right)}, & |r-r_0|\leq\frac{1}{2}\\0, & \text{otherwise}\end{cases} $.
Comments:
- The computation for $ r_0 $ is wrong. The correct expression of $ r_0 $ should be: $ r_0 = \sqrt{2}\sin(\frac{\pi}{4}-\theta) $. It can also be expressed as: $ r_0=\cos\theta+\sin\theta $.
- The rest statement is correct, and then the final result becomes: $ p_{\theta}(r)=\begin{cases}\sqrt{1-4(r-r_0)}, & |r-r_0|\leq\frac{1}{2}\\0, & \text{otherwise} \end{cases} $.
e)
$ \begin{align} f(x,y) & =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(\mu,\nu)e^{2\pi j(x\mu+y\nu)}d\mu d\nu\\ & = \int_{-\infty}^{\infty}\int_{0}^{\pi}p_\theta(\rho)e^{2\pi j(x\rho\text{cos}\theta+y\rho\text{sin}\theta)}|\rho|d\theta d\rho\\ & = \int_{0}^{\pi}\underbrace{\int_{-\infty}^{\infty}|\rho|p_\theta(\rho)e^{2\pi j(x\rho\text{cos}\theta+y\rho\text{sin}\theta)}d\rho}_{g_\theta(x\text{cos}\theta+y\text{sin}\theta)}d\theta \end{align} $
So $ g_\theta(t) $ is given by:
$ g_\theta(t)=\int_{-\infty}^{\infty}|\rho|p_\theta(\rho)e^{2\pi j\rho t}d\rho=\text{CTFT}^{-1}\{|\rho|p_\theta(\rho)\}=h(t)\ast p_\theta(r) $
So what we do is:
- measure projection $ p_\theta(r) $;
- filter the projection $ g_\theta(r)=h(r)\ast p_\theta(r) $;
- back project filtered projection: $ f(x,y)=\int_0^{\pi}g_\theta(x\text{cos}\theta)+y\text{sin}\theta)d\theta $.
Related Problems
a) Calculate the forward projection $ p_\theta(r) $, for $ f(x,y)=\text{rect}(x,y) $, as $ \theta=0 $ and $ \theta=\pi/4 $.
b) Calculate the forward projection $ p_\theta(r) $, for $ f(x,y)=\delta(x-a,y-b) $.
"Communication, Networks, Signal, and Image Processing" (CS)- Question 5, August 2011
Go to
- Part 1: solutions and discussions
- Part 2: solutions and discussions