| (One intermediate revision by the same user not shown) | |||
| Line 212: | Line 212: | ||
---- | ---- | ||
| − | <math>(4)\ | + | <math>(4)\ (cos\omega_0 n)u[n]</math> |
Compute Z transform | Compute Z transform | ||
| Line 218: | Line 218: | ||
<math>\begin{align} | <math>\begin{align} | ||
X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ | X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ | ||
| − | &= \sum_{n=-\infty}^{\infty} | + | &= \sum_{n=-\infty}^{\infty} (cos\omega_0 n)u[n]z^{-n} \\ |
&= \sum_{n=0}^{\infty} \frac{e^{j\omega_0n}+e^{-j\omega_0n}}{2}z^{-n} \\ | &= \sum_{n=0}^{\infty} \frac{e^{j\omega_0n}+e^{-j\omega_0n}}{2}z^{-n} \\ | ||
&= \frac{1}{2}[\sum_{n=0}^{\infty}e^{j\omega_0n}z^{-n} + \sum_{n=0}^{\infty}e^{-j\omega_0n}z^{-n}] \\ | &= \frac{1}{2}[\sum_{n=0}^{\infty}e^{j\omega_0n}z^{-n} + \sum_{n=0}^{\infty}e^{-j\omega_0n}z^{-n}] \\ | ||
| Line 233: | Line 233: | ||
X(z)&= \frac{1}{2}\frac{1-e^{j\omega_0}z^{-1} + 1-e^{-j\omega_0}z^{-1}}{(1-e^{j\omega_0}z^{-1})(1-e^{-j\omega_0}z^{-1})} \\ | X(z)&= \frac{1}{2}\frac{1-e^{j\omega_0}z^{-1} + 1-e^{-j\omega_0}z^{-1}}{(1-e^{j\omega_0}z^{-1})(1-e^{-j\omega_0}z^{-1})} \\ | ||
&= \frac{1}{2}\frac{2-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}}{1-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}+z^{-2}} \\ | &= \frac{1}{2}\frac{2-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}}{1-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}+z^{-2}} \\ | ||
| − | &= \frac{1}{2}\frac{2- | + | &= \frac{1}{2}\frac{2-2(cos\omega_0)z^{-1}}{1-(2cos\omega_0)z^{-1}+z^{-2}} \\ |
&= \frac{1-(cos\omega_0)z^{-1}}{1-(2cos\omega_0)z^{-1}+z^{-2}} | &= \frac{1-(cos\omega_0)z^{-1}}{1-(2cos\omega_0)z^{-1}+z^{-2}} | ||
\end{align}</math> | \end{align}</math> | ||
| Line 240: | Line 240: | ||
Compute Inverse Z transform | Compute Inverse Z transform | ||
| − | The power series expansion of the given function is | + | We can use partial fraction expansion to rewrite the z transform in a form similar to (1), (2). (See [[Partial_Fraction_Expansion|here]] for a general review of partial fraction expansion) |
| + | |||
| + | Then we can use power series expansion (in this case: geometric series) and by comparison, we can obtain its z inverse transform. | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X(z) &= \frac{1-\frac{e^{j\omega_0}+e^{-j\omega_0}}{2}z^{-1}}{1-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}+z^{-2}},\ |z|>a \\ | ||
| + | &= \frac{1}{2}\frac{2-2(cos\omega_0)z^{-1}}{(1-e^{j\omega_0}z^{-1})(1-e^{-j\omega_0}z^{-1})} \\ | ||
| + | &= \frac{1}{2}[\frac{1}{1-e^{j\omega_0}z^{-1}} + \frac{1}{1-e^{-j\omega_0}z^{-1}}] \\ | ||
| + | &= \frac{1}{2}[\sum_{n=0}^{\infty}e^{j\omega_0n}z^{-n} + \sum_{n=0}^{\infty}e^{-j\omega_0n}z^{-n}] \\ | ||
| + | &= \sum_{n=0}^{\infty} \frac{e^{j\omega_0n}+e^{-j\omega_0n}}{2}z^{-n} \\ | ||
| + | &= \sum_{n=-\infty}^{\infty} cos(\omega_0 n)u[n]z^{-n},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} | ||
| + | \end{align}</math> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | x[n] &= (cos\omega_0 n)u[n] | ||
| + | \end{align}</math> | ||
| + | |||
| + | ---- | ||
| + | (5) Compute Z transform of | ||
| + | |||
| + | <math>x[n]=nu[n]</math> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ | ||
| + | &= \sum_{n=-\infty}^{\infty} nu[n]z^{-n} \\ | ||
| + | &= \sum_{n=0}^{\infty} nz^{-n} | ||
| + | \end{align}</math> | ||
| + | |||
| + | Let <math>k=\frac{1}{z}</math> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X(k) &= \sum_{n=0}^{\infty} nk^{n} \\ | ||
| + | &= k\sum_{n=0}^{\infty} nk^{n-1} \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | We know that | ||
| + | |||
| + | <math>\sum_{n=0}^{\infty} k^{n} = \frac{1}{1-k},\ |k|<1</math> | ||
| + | |||
| + | Compute derivative with respect to k on both side we have | ||
| + | |||
| + | <math>\sum_{n=0}^{\infty} nk^{n-1} = \frac{1}{(1-k)^2},\ |k|<1</math> | ||
| + | |||
| + | Therefore | ||
| + | |||
| + | <math>X(k)=\frac{k}{(1-k)^2},\ |k|<1</math> | ||
| + | |||
| + | <math>X(z)=\frac{z^{-1}}{(1-z^{-1})^2},\ \text{with ROC }|z|>1</math> | ||
| + | |||
| + | ---- | ||
| + | (6) Compute inverse Z transform of | ||
| + | |||
| + | <math>X(z) = \log \left( 1+z \right), \quad |z|<1 </math>. | ||
| + | |||
| + | expand the function into a power series using either the Taylor series formula or a [[PowerSeriesFormulas|table of power series formulas]]. | ||
| + | |||
| + | The power series expansion of the given function is: | ||
<math>\begin{align} | <math>\begin{align} | ||
| − | X(z) &= | + | X(z) &= \sum_{n=1}^{\infty} (-1)^{n+1} \frac{z^n}{n}, \ -1 < z \le 1 \\ |
| − | &= | + | &= \sum_{n=-\infty}^{\infty} (-1)^{n+1} u[n-1] \frac{z^n}{n} |
\end{align}</math> | \end{align}</math> | ||
| − | Substitute n= | + | Substitute n = -k |
<math>\begin{align} | <math>\begin{align} | ||
| − | X(z) &= | + | X(z) &= \sum_{k=-\infty}^{\infty} (-1)^{-k+1} u[-k-1] \frac{z^{-k}}{-k} \\ |
| − | &= \sum_{ | + | &= \sum_{k=-\infty}^{\infty} \frac{(-1)^{-k+1}}{-k} u[-k-1]z^{-k} \\ |
| + | &= \sum_{k=-\infty}^{\infty} \frac{(-1)^{-k}(-1)}{-k} u[-k-1] z^{-k} \\ | ||
| + | &= \sum_{k=-\infty}^{\infty}\frac{(-1)^{-k}}{k} u[-k-1]z^{-k}, \text{ and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} | ||
\end{align}</math> | \end{align}</math> | ||
<math>\begin{align} | <math>\begin{align} | ||
| − | x[n] &= | + | x[n] &= \frac{(-1)^{-n}}{n} u[-n-1] \\ |
| + | &= \frac{(-1)^{n}}{n} u[-n-1] | ||
\end{align}</math> | \end{align}</math> | ||
Latest revision as of 04:33, 14 September 2011
Homework 2, ECE438, Fall 2011, Prof. Boutin
Question 1
Pick a note frequency f0 = 392Hz
| x(t) = 'cos'(2πf0t) = 'cos'(2π * 392t) |
| $ a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000} $ |
| $ 2f_0<\frac{1}{T_1}, \ No\ aliasing\ occurs. $ |
$ \begin{align} x_1(n) &=x(nT_1)=cos(2\pi *392nT_1)=cos(2\pi *\frac{392}{1000}n) \\ &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{1000}n} + e^{j2\pi *\frac{392}{1000}n} \right) \\ \end{align} $
| $ 0<2\pi *\frac{392}{1000}<\pi $ |
| $ -\pi<-2\pi *\frac{392}{1000}<0 $ |
$ \begin{align} \mathcal{X}_1(\omega) &=2\pi *\frac{1}{2} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ &=\pi \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ \end{align} $
| $ for\ all\ \omega $ |
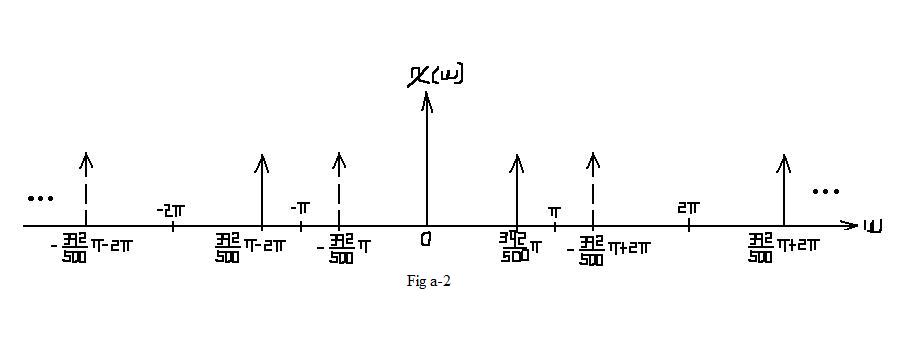
| $ \mathcal{X}_1(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] $ |
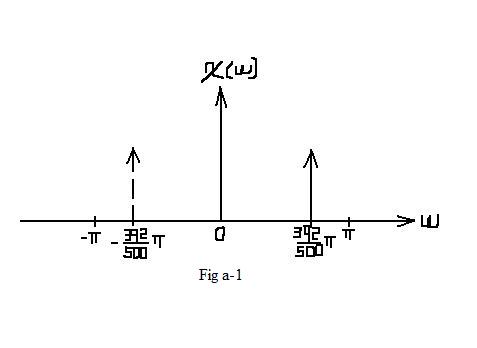
| In this situation, no aliasing occurs. In the interval of [ − π,π], which represents one period, the frequcy spectrum remains the same as Fig a-1. |
| $ b.\ Assign\ sampling\ period\ T_2=\frac{1}{500} $ |
| $ 2f_0>\frac{1}{T_2}, \ Aliasing\ occurs. $ |
$ \begin{align} x_2(n) &=x(nT_2)=cos(2\pi *392nT_2)=cos(2\pi *\frac{392}{500}n) \\ &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{500}n} + e^{j2\pi *\frac{392}{500}n} \right) \\ \end{align} $
| $ \pi<2\pi *\frac{392}{500}<2\pi $ |
| $ -2\pi<-2\pi *\frac{392}{500}<\pi $ |
| $ \mathcal{X}_2(\omega)=\pi \left[\delta (\omega -2\pi *\frac{392}{500}) + \delta (\omega + 2\pi *\frac{392}{500})\right] $ |
| $ X_2(f)=\frac{1}{2}\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right] $ |
| $ for\ all\ \omega $ |
| $ \mathcal{X}_2(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{500}) + \delta (\omega + 2\pi *\frac{392}{500})\right] $ |
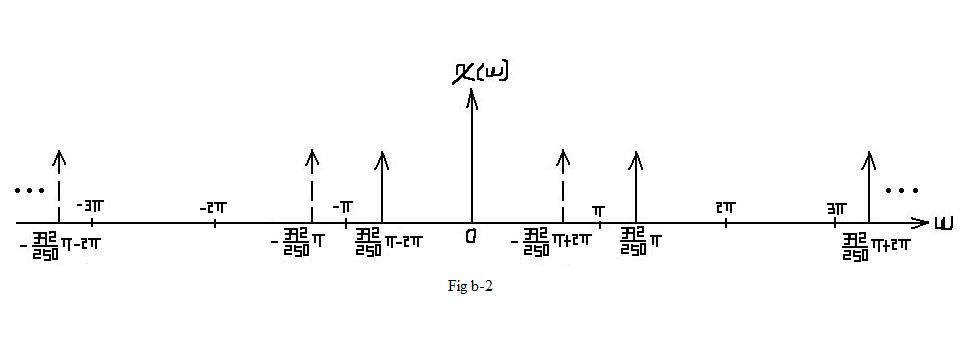
| $ X_2(f)=\frac{1}{2}rep_2\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right] $ |
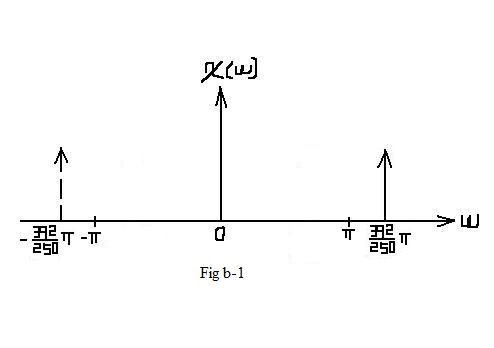
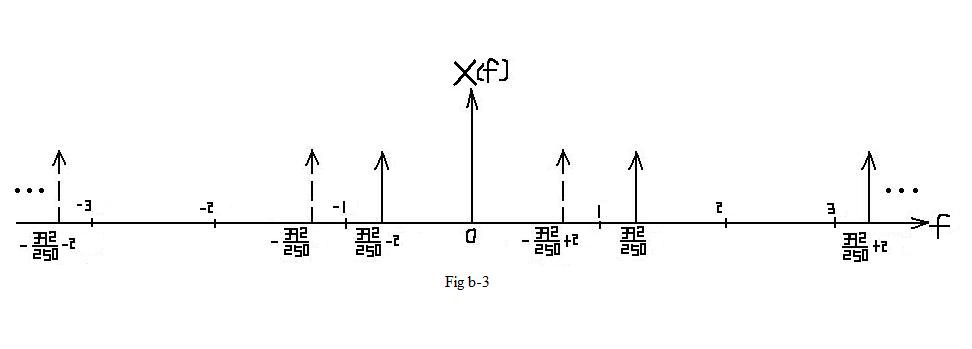
| In this situation, aliasing DO occurs. In the interval of [ − π,π], which represents one period, the frequcy spectrum is different from Fig b-1. |
Question 2
$ (1)\ x[n]=a^{n+1}u[n-1],\ a>0 $
Compute Z transform
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ &= \sum_{n=-\infty}^{\infty} a^{n+1} u[n-1]z^{-n} \\ &= a\sum_{n=1}^{\infty} a^{n}z^{-n} \\ &= \frac{a^2z^{-1}}{1-az^{-1}} \end{align} $
with ROC: $ |z|>a $
Compute Inverse Z transform
The power series expansion of the given function is
$ \begin{align} X(z) &= a^2 z^{-1}\sum_{n=0}^{\infty} a^n z^{-n},\ |z|>a \\ &= a\sum_{n=0}^{\infty} a^{n+1}z^{-n-1} \end{align} $
Substitute n=m-1
$ \begin{align} X(z) &= a\sum_{m=1}^{\infty} a^{m}z^{-m} \\ &= \sum_{m=-\infty}^{\infty} a^{m+1}u[m-1]z^{-m},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} \end{align} $
$ \begin{align} x[n] &= a^{n+1} u[n-1] \end{align} $
$ (2)\ x[n]=-a^{n}u[-n-1],\ a>0 $
Compute Z transform
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ &= -\sum_{n=-\infty}^{\infty} a^{n} u[-n-1]z^{-n} \\ &= -\sum_{n=-\infty}^{-1} a^{n}z^{-n} \\ \end{align} $
Substitute m=-n
$ \begin{align} X(z) &= -\sum_{n=1}^{\infty} a^{-n}z^{n} \\ &= -\frac{a^{-1}z}{1-a^{-1}z} \\ &= \frac{1}{1-az^{-1}} \end{align} $
with ROC: $ |z|<a $
Compute Inverse Z transform
$ \begin{align} X(z) &= \frac{1}{1-az^{-1}} \\ &= \frac{a^{-1}z}{a^{-1}z-1} \\ &= -a^{-1}z\frac{1}{1-a^{-1}z} \end{align} $
The power series expansion of the given function is
$ \begin{align} X(z) &= -a^{-1}z\sum_{n=0}^{\infty} a^{-n}z^{n} \\ &= -\sum_{n=0}^{\infty} a^{-n-1}z^{n+1} \\ \end{align} $
Substitute n+1=-m
$ \begin{align} X(z) &= -\sum_{m=-1}^{-\infty} a^{m}z^{-m} \\ &= -\sum_{m=-\infty}^{\infty} a^{m}u[-m-1]z^{-m},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} \end{align} $
$ \ x[n]=-a^{n}u[-n-1],\ a>0 $
$ (3) x[n]=u[n+1]-u[n-1] $
Compute Z transform
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ &= \sum_{n=-\infty}^{\infty} (u[n+1]-u[n-1])z^{-n} \\ &= \sum_{n=-1}^{1} z^{-n} \\ &= 1+z^{-1}+z^1 \end{align} $
with ROC: $ z\in R,\ z\neq 0 $
Compute Inverse Z transform
$ \text{Since }z^k=\delta[n-k]z^n $
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty}\sum_{k=-1}^{1} \delta[n-k] z^{n},\ z\in R,\ z\neq 0 \\ &= \sum_{n=-\infty}^{\infty} (\delta[n+1]+\delta[n]+\delta[n-1])z^{n} \\ \end{align} $
Substitute n=-m
$ \begin{align} X(z) &= \sum_{m=-\infty}^{\infty} (\delta[-m+1]+\delta[-m]+\delta[-m-1])z^{-m},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} \end{align} $
$ \begin{align} x[n] &= \delta[-n+1]+\delta[-n]+\delta[-n-1] \\ &= u[n+1]-u[n-1] \end{align} $
$ (4)\ (cos\omega_0 n)u[n] $
Compute Z transform
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ &= \sum_{n=-\infty}^{\infty} (cos\omega_0 n)u[n]z^{-n} \\ &= \sum_{n=0}^{\infty} \frac{e^{j\omega_0n}+e^{-j\omega_0n}}{2}z^{-n} \\ &= \frac{1}{2}[\sum_{n=0}^{\infty}e^{j\omega_0n}z^{-n} + \sum_{n=0}^{\infty}e^{-j\omega_0n}z^{-n}] \\ &= \frac{1}{2}[\frac{1}{1-e^{j\omega_0}z^{-1}} + \frac{1}{1-e^{-j\omega_0}z^{-1}} ] \end{align} $
with ROC: $ |z|>|e^{j\omega_0}|,\ \text{and }|z|>|e^{-j\omega_0}| $
i.e. $ |z|>1 $
Simplify the answer
$ \begin{align} X(z)&= \frac{1}{2}\frac{1-e^{j\omega_0}z^{-1} + 1-e^{-j\omega_0}z^{-1}}{(1-e^{j\omega_0}z^{-1})(1-e^{-j\omega_0}z^{-1})} \\ &= \frac{1}{2}\frac{2-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}}{1-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}+z^{-2}} \\ &= \frac{1}{2}\frac{2-2(cos\omega_0)z^{-1}}{1-(2cos\omega_0)z^{-1}+z^{-2}} \\ &= \frac{1-(cos\omega_0)z^{-1}}{1-(2cos\omega_0)z^{-1}+z^{-2}} \end{align} $
Compute Inverse Z transform
We can use partial fraction expansion to rewrite the z transform in a form similar to (1), (2). (See here for a general review of partial fraction expansion)
Then we can use power series expansion (in this case: geometric series) and by comparison, we can obtain its z inverse transform.
$ \begin{align} X(z) &= \frac{1-\frac{e^{j\omega_0}+e^{-j\omega_0}}{2}z^{-1}}{1-(e^{j\omega_0}+e^{-j\omega_0})z^{-1}+z^{-2}},\ |z|>a \\ &= \frac{1}{2}\frac{2-2(cos\omega_0)z^{-1}}{(1-e^{j\omega_0}z^{-1})(1-e^{-j\omega_0}z^{-1})} \\ &= \frac{1}{2}[\frac{1}{1-e^{j\omega_0}z^{-1}} + \frac{1}{1-e^{-j\omega_0}z^{-1}}] \\ &= \frac{1}{2}[\sum_{n=0}^{\infty}e^{j\omega_0n}z^{-n} + \sum_{n=0}^{\infty}e^{-j\omega_0n}z^{-n}] \\ &= \sum_{n=0}^{\infty} \frac{e^{j\omega_0n}+e^{-j\omega_0n}}{2}z^{-n} \\ &= \sum_{n=-\infty}^{\infty} cos(\omega_0 n)u[n]z^{-n},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} \end{align} $
$ \begin{align} x[n] &= (cos\omega_0 n)u[n] \end{align} $
(5) Compute Z transform of
$ x[n]=nu[n] $
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ &= \sum_{n=-\infty}^{\infty} nu[n]z^{-n} \\ &= \sum_{n=0}^{\infty} nz^{-n} \end{align} $
Let $ k=\frac{1}{z} $
$ \begin{align} X(k) &= \sum_{n=0}^{\infty} nk^{n} \\ &= k\sum_{n=0}^{\infty} nk^{n-1} \\ \end{align} $
We know that
$ \sum_{n=0}^{\infty} k^{n} = \frac{1}{1-k},\ |k|<1 $
Compute derivative with respect to k on both side we have
$ \sum_{n=0}^{\infty} nk^{n-1} = \frac{1}{(1-k)^2},\ |k|<1 $
Therefore
$ X(k)=\frac{k}{(1-k)^2},\ |k|<1 $
$ X(z)=\frac{z^{-1}}{(1-z^{-1})^2},\ \text{with ROC }|z|>1 $
(6) Compute inverse Z transform of
$ X(z) = \log \left( 1+z \right), \quad |z|<1 $.
expand the function into a power series using either the Taylor series formula or a table of power series formulas.
The power series expansion of the given function is:
$ \begin{align} X(z) &= \sum_{n=1}^{\infty} (-1)^{n+1} \frac{z^n}{n}, \ -1 < z \le 1 \\ &= \sum_{n=-\infty}^{\infty} (-1)^{n+1} u[n-1] \frac{z^n}{n} \end{align} $
Substitute n = -k
$ \begin{align} X(z) &= \sum_{k=-\infty}^{\infty} (-1)^{-k+1} u[-k-1] \frac{z^{-k}}{-k} \\ &= \sum_{k=-\infty}^{\infty} \frac{(-1)^{-k+1}}{-k} u[-k-1]z^{-k} \\ &= \sum_{k=-\infty}^{\infty} \frac{(-1)^{-k}(-1)}{-k} u[-k-1] z^{-k} \\ &= \sum_{k=-\infty}^{\infty}\frac{(-1)^{-k}}{k} u[-k-1]z^{-k}, \text{ and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} \end{align} $
$ \begin{align} x[n] &= \frac{(-1)^{-n}}{n} u[-n-1] \\ &= \frac{(-1)^{n}}{n} u[-n-1] \end{align} $