| (4 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | =Homework 9 Solutions, [[2011 Spring ECE 301 Boutin|ECE301 Spring 2011 Prof. Boutin]]= | + | = Homework 9 Solutions, [[2011 Spring ECE 301 Boutin|ECE301 Spring 2011 Prof. Boutin]] = |
| − | Students should feel free to make comments/corrections or ask questions directly on this page. | + | Students should feel free to make comments/corrections or ask questions directly on this page. |
| − | ==Question 1== | + | == Question 1 == |
| − | + | ||
| − | ( | + | (a) The given signal has finite duration and hence it is '''not band-limited'''. |
| − | ( | + | (b) The given signal has finite duration and hence it is '''not band-limited'''. |
| − | <math>x(t)=\frac{\sin(3\pi t)}{t}=\pi\frac{\sin(3\pi t)}{\pi t}</math> | + | (c) The given signal has infinite duration and hence it is '''band-limited'''. |
| + | |||
| + | <math>x(t)=\frac{\sin(3\pi t)}{t}=\pi\frac{\sin(3\pi t)}{\pi t}</math> | ||
<math> | <math> | ||
| Line 19: | Line 20: | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
\end{array}\right. | \end{array}\right. | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Thus the Nyquist rate of this signal is < | + | Thus the Nyquist rate of this signal is <span class="texhtml">ω<sub>''s''</sub> = 2(3π) = 6π</span>. |
| − | <font color="blue"> | + | <font color="blue">QUESTION: I know that the answer to this isn't necessary to answer the question, but if the transform pair says that <br> <math>\frac{2 \sin \left( W t \right)}{\pi t } \ </math> transforms to <math>\left\{\begin{array}{ll}1, & \text{ if }|\omega| <W,\\ 0, & \text{else.}\end{array} \right. \ </math>, <br><br> then why does the F.Transform not account for the factor of "2" in front in the answers above and below? <br><br> Should the answers not take the following form: <br> <math> |
| − | QUESTION: I know that the answer to this isn't necessary to answer the question, but if the transform pair says that <br> | + | |
| − | <math>\frac{2 \sin \left( W t \right)}{\pi t } \ </math> | + | |
| − | then why does the F.Transform not account for the factor of "2" in front in the answers above and below? <br><br> | + | |
| − | Should the answers not take the following form: <br> | + | |
| − | <math> | + | |
\begin{align} | \begin{align} | ||
\mathcal{X}(\omega)&=\pi/2 \cdot \mathfrak{F}\left\{\frac{2\sin(3\pi t)}{\pi t}\right\} \\ | \mathcal{X}(\omega)&=\pi/2 \cdot \mathfrak{F}\left\{\frac{2\sin(3\pi t)}{\pi t}\right\} \\ | ||
| Line 36: | Line 31: | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
\end{array}\right. | \end{array}\right. | ||
| − | \end{align} | + | \end{align}</math> <br>? </font> <br><br> |
| − | </math> | + | |
| − | <br>? | + | |
| − | </font> | + | |
| − | <br><br> | + | |
| − | <font color="red"> | + | <font color="red">There was a typo in the CTFT pairs posted. There is no inherent '2' in the equation for the pair. To reference, the book will confirm this in the tables around page 329. </font> <br><br> |
| − | There was a typo in the CTFT pairs posted. There is no inherent '2' in the equation for the pair. To reference, the book will confirm this in the tables around page 329. | + | |
| − | </font> | + | |
| − | <br><br> | + | |
| + | <br> (d) The given signal has infinite duration and hence it is '''band-limited'''. | ||
| − | + | <font color="red">Instructor's note: it is not always the case that infinite duration signals are band-limited. However, it is true that finite duration signals are never band-limited. -pm </font> | |
| − | + | <math>x(t)=\frac{\sin(3\pi(t+5))}{t+5}=\pi\frac{\sin(3\pi(t+5))}{\pi(t+5)}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <math>x(t)=\frac{\sin(3\pi(t+5))}{t+5}=\pi\frac{\sin(3\pi(t+5))}{\pi(t+5)}</math> | + | |
<math> | <math> | ||
| Line 63: | Line 48: | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
\end{array}\right. | \end{array}\right. | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Thus the Nyquist rate of this signal is < | + | Thus the Nyquist rate of this signal is <span class="texhtml">ω<sub>''s''</sub> = 2(3π) = 6π</span>. |
| − | + | ||
| − | + | == Question 2 == | |
| − | Using frequency shift property of FT, we get: | + | <math>x(t)=e^{j\pi t}\frac{\sin(\pi t)}{t}=\pi e^{j\pi t}\frac{\sin(\pi t)}{\pi t}</math> |
| + | |||
| + | Using frequency shift property of FT, we get: | ||
<math> | <math> | ||
| Line 87: | Line 72: | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
\end{array}\right. | \end{array}\right. | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | The figure below shows the plot of the FT of < | + | The figure below shows the plot of the FT of <span class="texhtml">''x''(''t'')</span>. |
| − | [[Image: | + | [[Image:301 sp2011 boutin hw9 figure1.jpg]] |
| − | After sampling with a sampling period T, we get: | + | After sampling with a sampling period T, we get: |
| − | <math>\mathcal{X}_s(\omega)=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{P}(\omega)=\frac{1}{T}\sum_{k=-\infty}^{\infty}\mathcal{X}(\omega-\frac{2\pi k}{T})</math> | + | <math>\mathcal{X}_s(\omega)=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{P}(\omega)=\frac{1}{T}\sum_{k=-\infty}^{\infty}\mathcal{X}(\omega-\frac{2\pi k}{T})</math> |
| − | (a) The FT of the signal after sampling with sampling period <math | + | (a) The FT of the signal after sampling with sampling period <math>T=\frac{1}{4}</math> is shown in the figure below. |
| − | [[Image: | + | [[Image:301 sp2011 boutin hw9 figure2.jpg]] |
| − | From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter: | + | :<font color="red"></font><font color="red"></font> |
| + | |||
| + | <font color="red"></font> | ||
| + | |||
| + | <font color="red">Instructor's note: Note that this is the Fourier transform of the CT signal representing the sampling in CT. The Fourier transform of the DT signal obtained by storing the values of the samples in an array, <span class="texhtml">''x''<sub>''d''</sub>[''n''] = ''x''(''n''''T'')</span> is a frequency-rescaled version of this graph (in such a way to obtain a signal that is periodic with period <span class="texhtml">2π</span>). -pm </font> | ||
| + | |||
| + | From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter: | ||
<math> | <math> | ||
| Line 108: | Line 98: | ||
\frac{1}{4} , & \mbox{ for } 0<\omega<2\pi \\ | \frac{1}{4} , & \mbox{ for } 0<\omega<2\pi \\ | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
| − | \end{array}\right. | + | \end{array}\right.</math> |
| − | </math> | + | |
| − | + | :<font color="red"></font><font color="red"></font> | |
| − | + | <font color="red"></font> | |
| − | From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter: | + | <font color="red">Instructor's note: To recover the signal from the sampling in DT, one must first convert the samples to a pulse-train, and then low-pass filter. -pm </font> |
| + | |||
| + | (b) The FT of the signal after sampling with sampling period <math>T=\frac{2}{3}</math> is shown in the figure below. | ||
| + | |||
| + | [[Image:301 sp2011 boutin hw9 figure3.jpg]] | ||
| + | |||
| + | From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter: | ||
<math> | <math> | ||
| Line 121: | Line 116: | ||
\frac{2}{3} , & \mbox{ for } 0<\omega<2\pi \\ | \frac{2}{3} , & \mbox{ for } 0<\omega<2\pi \\ | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
| − | \end{array}\right. | + | \end{array}\right.</math> |
| − | </math> | + | |
| − | (c) The FT of the signal after sampling with sampling period < | + | (c) The FT of the signal after sampling with sampling period <span class="texhtml">''T'' = 2</span> is shown in the figure below. |
| − | [[Image: | + | [[Image:301 sp2011 boutin hw9 figure4.jpg]] |
| − | From the figure, we can see that there is aliasing and thus the signal cannot be recovered. | + | From the figure, we can see that there is aliasing and thus the signal cannot be recovered. |
| − | ==Question 3== | + | == Question 3 == |
<math> | <math> | ||
| Line 137: | Line 131: | ||
&=\omega_se^{-3j\omega}\sum_{k=-\infty}^{\infty} \delta(\omega-\omega_s k) \\ | &=\omega_se^{-3j\omega}\sum_{k=-\infty}^{\infty} \delta(\omega-\omega_s k) \\ | ||
&=\omega_s \sum_{k=-\infty}^{\infty} e^{-3j\omega_s k}\delta(\omega-\omega_s k) \text{ Using sampling property of dirac-delta function} | &=\omega_s \sum_{k=-\infty}^{\infty} e^{-3j\omega_s k}\delta(\omega-\omega_s k) \text{ Using sampling property of dirac-delta function} | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Let < | + | Let <span class="texhtml">''x''<sub>''s''</sub>(''t'') = ''x''(''t'')''p''(''t'' − 3)</span>, then |
<math> | <math> | ||
| Line 146: | Line 139: | ||
\mathcal{X}_s(\omega)&=\frac{\omega_s}{2\pi} \mathcal{X}(\omega)*\sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\delta(\omega-\omega_s k) \\ | \mathcal{X}_s(\omega)&=\frac{\omega_s}{2\pi} \mathcal{X}(\omega)*\sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\delta(\omega-\omega_s k) \\ | ||
&=\frac{\omega_s}{2\pi} \sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\mathcal{X}(\omega-\omega_s k) \\ | &=\frac{\omega_s}{2\pi} \sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\mathcal{X}(\omega-\omega_s k) \\ | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Note that the exponential term does not depend on < | + | Note that the exponential term does not depend on <span class="texhtml">ω</span>, and that at <span class="texhtml">''k'' = 0</span> it is 1. Thus: |
| − | ::if < | + | |
| + | ::if <span class="texhtml">ω<sub>''s''</sub> > 2ω<sub>''M''</sub></span>, then the signal can be recovered by passing <span class="texhtml">''x''<sub>''s''</sub>(''t'')</span> through the following filter: | ||
::<math> | ::<math> | ||
| Line 156: | Line 149: | ||
\frac{2\pi}{\omega_s} , & \mbox{ for } |\omega|<\omega_M \\ | \frac{2\pi}{\omega_s} , & \mbox{ for } |\omega|<\omega_M \\ | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
| − | \end{array}\right. | + | \end{array}\right.</math> |
| − | </math> | + | |
| − | ::if < | + | ::if <span class="texhtml">ω<sub>''s''</sub> < 2ω<sub>''M''</sub></span>, then there will be aliasing and the signal cannot be recovered. |
| + | === What is ωm in this filter? I thought the cutoff for the filter needed to be ωc, where ωm < ωc < ωs - ωm, in order to remove all of the copies but retain the main signal. === | ||
| − | == | + | === --[[User:Kellsper|Kellsper]] 19:44, 21 April 2011 (UTC)<br> === |
| − | + | :<span style="color:blue">TA's comment: Yes, that is true. In this case <math>\omega_c=\omega_M</math>.</span> | |
| − | + | == Question 4 == | |
| − | < | + | Since <span class="texhtml">''x''(''t'')</span> is sampled with a sampling period <span class="texhtml">''T''<sub>''s''</sub> = π / ω<sub>0</sub></span>, then the sampling rate is <span class="texhtml">ω<sub>''s''</sub> = 2ω<sub>0</sub></span> and hence there is no aliasing. |
| − | + | Taking the FT of both sides of the system equation we get: | |
| − | <math>\mathcal{ | + | <math>\mathcal{Y}(\omega)=j\omega\mathcal{X}(\omega)</math> |
| + | and hence the frequency response of the CT system is: | ||
| − | Using the relationship between the frequency response of the CT system and the DT system, we get: | + | <math>\mathcal{H}(\omega)=j\omega</math> |
| + | |||
| + | <br> Using the relationship between the frequency response of the CT system and the DT system, we get: | ||
<math>\begin{align} | <math>\begin{align} | ||
\mathcal{H}_d(\omega)&=\mathcal{H}(\frac{\omega}{T_s}) \text{ for }|\omega|<\pi \\ | \mathcal{H}_d(\omega)&=\mathcal{H}(\frac{\omega}{T_s}) \text{ for }|\omega|<\pi \\ | ||
&=j\frac{\omega}{T_s} \text{ for }|\omega|<\pi | &=j\frac{\omega}{T_s} \text{ for }|\omega|<\pi | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Now in order to get the impulse response of the DT system we take the IDTFT of the frequency response above: | + | Now in order to get the impulse response of the DT system we take the IDTFT of the frequency response above: |
<math>\begin{align} | <math>\begin{align} | ||
| Line 187: | Line 182: | ||
&=\frac{j}{2\pi T_s} \int_{-\pi}^{\pi} \omega e^{j\omega n}d\omega \\ | &=\frac{j}{2\pi T_s} \int_{-\pi}^{\pi} \omega e^{j\omega n}d\omega \\ | ||
&=\frac{j}{2\pi T_s} \left[\omega \frac{e^{j\omega n}}{jn}\right]^{\pi}_{-\pi} + \frac{j}{2\pi T_s}\left[\frac{e^{j\omega n}}{n^2}\right]_{-\pi}^{\pi} \\ | &=\frac{j}{2\pi T_s} \left[\omega \frac{e^{j\omega n}}{jn}\right]^{\pi}_{-\pi} + \frac{j}{2\pi T_s}\left[\frac{e^{j\omega n}}{n^2}\right]_{-\pi}^{\pi} \\ | ||
| − | &=\frac{1}{2T_s n} [e^{j | + | &=\frac{1}{2T_s n} [e^{j \pi n}+e^{-j \pi n} ] + \frac{j}{2\pi T_s n^2}[e^{j \pi n} - e^{-j \pi n}] \\ |
&=\frac{(-1)^n}{T_s n} \\ | &=\frac{(-1)^n}{T_s n} \\ | ||
&=\frac{\omega_0 (-1)^n}{\pi n} | &=\frac{\omega_0 (-1)^n}{\pi n} | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| + | Note that an impulse response is sufficient to characterize an LTI system. | ||
| − | |||
---- | ---- | ||
| − | [[HW9 ECE301 Spring2011 Prof Boutin| HW9]] | + | |
| + | [[HW9 ECE301 Spring2011 Prof Boutin|HW9]] | ||
[[2011 Spring ECE 301 Boutin|Back to 2011 Spring ECE 301 Boutin]] | [[2011 Spring ECE 301 Boutin|Back to 2011 Spring ECE 301 Boutin]] | ||
[[Category:2011_Spring_ECE_301_Boutin]] | [[Category:2011_Spring_ECE_301_Boutin]] | ||
Latest revision as of 06:01, 22 April 2011
Homework 9 Solutions, ECE301 Spring 2011 Prof. Boutin
Students should feel free to make comments/corrections or ask questions directly on this page.
Question 1
(a) The given signal has finite duration and hence it is not band-limited.
(b) The given signal has finite duration and hence it is not band-limited.
(c) The given signal has infinite duration and hence it is band-limited.
$ x(t)=\frac{\sin(3\pi t)}{t}=\pi\frac{\sin(3\pi t)}{\pi t} $
$ \begin{align} \mathcal{X}(\omega)&=\pi \cdot \mathfrak{F}\left\{\frac{\sin(3\pi t)}{\pi t}\right\} \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
Thus the Nyquist rate of this signal is ωs = 2(3π) = 6π.
QUESTION: I know that the answer to this isn't necessary to answer the question, but if the transform pair says that
$ \frac{2 \sin \left( W t \right)}{\pi t } \ $ transforms to $ \left\{\begin{array}{ll}1, & \text{ if }|\omega| <W,\\ 0, & \text{else.}\end{array} \right. \ $,
then why does the F.Transform not account for the factor of "2" in front in the answers above and below?
Should the answers not take the following form:
$ \begin{align} \mathcal{X}(\omega)&=\pi/2 \cdot \mathfrak{F}\left\{\frac{2\sin(3\pi t)}{\pi t}\right\} \\ &=\left\{\begin{array}{ll} \pi/2 , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
?
There was a typo in the CTFT pairs posted. There is no inherent '2' in the equation for the pair. To reference, the book will confirm this in the tables around page 329.
(d) The given signal has infinite duration and hence it is band-limited.
Instructor's note: it is not always the case that infinite duration signals are band-limited. However, it is true that finite duration signals are never band-limited. -pm
$ x(t)=\frac{\sin(3\pi(t+5))}{t+5}=\pi\frac{\sin(3\pi(t+5))}{\pi(t+5)} $
$ \begin{align} \mathcal{X}(\omega)&=\pi \cdot \mathfrak{F}\left\{\frac{\sin(3\pi (t+5))}{\pi (t+5)}\right\} \\ &=\left\{\begin{array}{ll} \pi e^{5j\omega} , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
Thus the Nyquist rate of this signal is ωs = 2(3π) = 6π.
Question 2
$ x(t)=e^{j\pi t}\frac{\sin(\pi t)}{t}=\pi e^{j\pi t}\frac{\sin(\pi t)}{\pi t} $
Using frequency shift property of FT, we get:
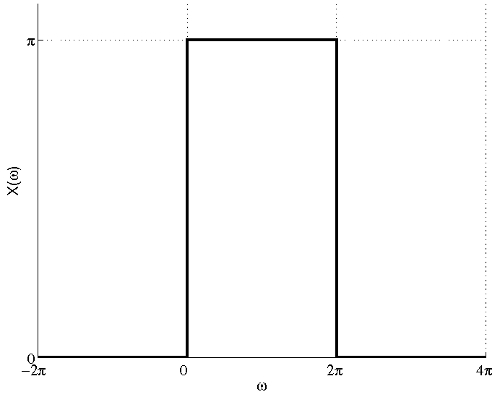
$ \begin{align} \mathcal{X}(\omega)&=\left\{\begin{array}{ll} \pi , & \mbox{ for } |\omega - \pi|<\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } -\pi <\omega-\pi<\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
The figure below shows the plot of the FT of x(t).
After sampling with a sampling period T, we get:
$ \mathcal{X}_s(\omega)=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{P}(\omega)=\frac{1}{T}\sum_{k=-\infty}^{\infty}\mathcal{X}(\omega-\frac{2\pi k}{T}) $
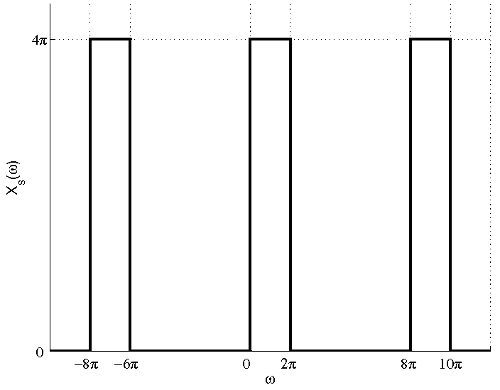
(a) The FT of the signal after sampling with sampling period $ T=\frac{1}{4} $ is shown in the figure below.
Instructor's note: Note that this is the Fourier transform of the CT signal representing the sampling in CT. The Fourier transform of the DT signal obtained by storing the values of the samples in an array, xd[n] = x(n'T) is a frequency-rescaled version of this graph (in such a way to obtain a signal that is periodic with period 2π). -pm
From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter:
$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{1}{4} , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. $
Instructor's note: To recover the signal from the sampling in DT, one must first convert the samples to a pulse-train, and then low-pass filter. -pm
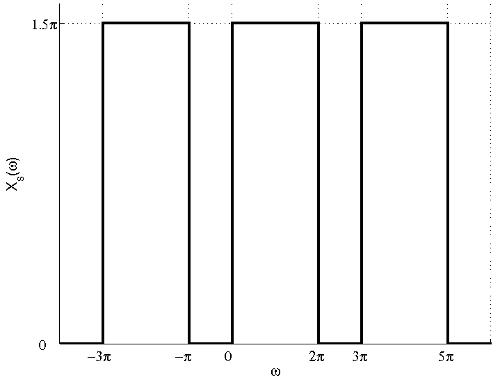
(b) The FT of the signal after sampling with sampling period $ T=\frac{2}{3} $ is shown in the figure below.
From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter:
$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{2}{3} , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. $
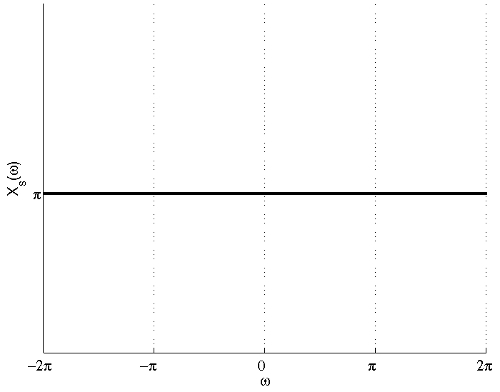
(c) The FT of the signal after sampling with sampling period T = 2 is shown in the figure below.
From the figure, we can see that there is aliasing and thus the signal cannot be recovered.
Question 3
$ \begin{align} \mathfrak{F}\left\{p(t-3)\right\}&=P(\omega)e^{-3j\omega} \\ &=\omega_se^{-3j\omega}\sum_{k=-\infty}^{\infty} \delta(\omega-\omega_s k) \\ &=\omega_s \sum_{k=-\infty}^{\infty} e^{-3j\omega_s k}\delta(\omega-\omega_s k) \text{ Using sampling property of dirac-delta function} \end{align} $
Let xs(t) = x(t)p(t − 3), then
$ \begin{align} \mathcal{X}_s(\omega)&=\frac{\omega_s}{2\pi} \mathcal{X}(\omega)*\sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\delta(\omega-\omega_s k) \\ &=\frac{\omega_s}{2\pi} \sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\mathcal{X}(\omega-\omega_s k) \\ \end{align} $
Note that the exponential term does not depend on ω, and that at k = 0 it is 1. Thus:
- if ωs > 2ωM, then the signal can be recovered by passing xs(t) through the following filter:
- $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{2\pi}{\omega_s} , & \mbox{ for } |\omega|<\omega_M \\ 0, & \mbox{ elsewhere} \end{array}\right. $
- if ωs < 2ωM, then there will be aliasing and the signal cannot be recovered.
What is ωm in this filter? I thought the cutoff for the filter needed to be ωc, where ωm < ωc < ωs - ωm, in order to remove all of the copies but retain the main signal.
--Kellsper 19:44, 21 April 2011 (UTC)
- TA's comment: Yes, that is true. In this case $ \omega_c=\omega_M $.
Question 4
Since x(t) is sampled with a sampling period Ts = π / ω0, then the sampling rate is ωs = 2ω0 and hence there is no aliasing.
Taking the FT of both sides of the system equation we get:
$ \mathcal{Y}(\omega)=j\omega\mathcal{X}(\omega) $
and hence the frequency response of the CT system is:
$ \mathcal{H}(\omega)=j\omega $
Using the relationship between the frequency response of the CT system and the DT system, we get:
$ \begin{align} \mathcal{H}_d(\omega)&=\mathcal{H}(\frac{\omega}{T_s}) \text{ for }|\omega|<\pi \\ &=j\frac{\omega}{T_s} \text{ for }|\omega|<\pi \end{align} $
Now in order to get the impulse response of the DT system we take the IDTFT of the frequency response above:
$ \begin{align} h_d[n]&=\frac{1}{2\pi}\int_{-\pi}^{\pi}j\frac{\omega}{T_s} e^{j\omega n} d\omega\\ &=\frac{j}{2\pi T_s} \int_{-\pi}^{\pi} \omega e^{j\omega n}d\omega \\ &=\frac{j}{2\pi T_s} \left[\omega \frac{e^{j\omega n}}{jn}\right]^{\pi}_{-\pi} + \frac{j}{2\pi T_s}\left[\frac{e^{j\omega n}}{n^2}\right]_{-\pi}^{\pi} \\ &=\frac{1}{2T_s n} [e^{j \pi n}+e^{-j \pi n} ] + \frac{j}{2\pi T_s n^2}[e^{j \pi n} - e^{-j \pi n}] \\ &=\frac{(-1)^n}{T_s n} \\ &=\frac{\omega_0 (-1)^n}{\pi n} \end{align} $
Note that an impulse response is sufficient to characterize an LTI system.