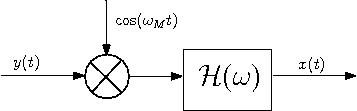| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | =Homework 10 Solutions, [[2011 Spring ECE 301 Boutin|ECE301 Spring 2011 Prof. Boutin]]= | + | = Homework 10 Solutions, [[2011 Spring ECE 301 Boutin|ECE301 Spring 2011 Prof. Boutin]] = |
| − | Students should feel free to make comments/corrections or ask questions directly on this page. | + | Students should feel free to make comments/corrections or ask questions directly on this page. |
| + | |||
| + | == Question 1 == | ||
| − | |||
a) We can write | a) We can write | ||
| + | |||
:<math>y_1(t)=e^{j \theta_c}x(t)e^{j\omega_c t}</math> | :<math>y_1(t)=e^{j \theta_c}x(t)e^{j\omega_c t}</math> | ||
| − | Notice that this is exactly as modulating by <math>e^{j\omega_c t}</math> but now we are multiplying with a complex exponential independent of < | + | Notice that this is exactly as modulating by <math>e^{j\omega_c t}</math> but now we are multiplying with a complex exponential independent of <span class="texhtml">''t''</span> (phase shift). We can recover the signal <span class="texhtml">''x''(''t'')</span> for any <span class="texhtml">ω<sub>''c''</sub></span>, and hence there are no conditions put on <span class="texhtml">ω<sub>''c''</sub></span>. |
| − | We can recover the signal < | + | |
| − | b) In order to recover signal < | + | b) In order to recover signal <span class="texhtml">''x''(''t'')</span>, we multiply <span class="texhtml">''y''<sub>1</sub>(''t'')</span> by <math>e^{-j(\omega_c t+\theta_c)}</math>. |
c) We can write | c) We can write | ||
| + | |||
:<math>y_2(t)=x(t)\left(\frac{e^{j\omega_c t}-e^{-j\omega_c t}}{2j}\right)</math> | :<math>y_2(t)=x(t)\left(\frac{e^{j\omega_c t}-e^{-j\omega_c t}}{2j}\right)</math> | ||
| − | Taking the FT of < | + | Taking the FT of <span class="texhtml">''y''<sub>2</sub>(''t'')</span>, we get: |
:<math>\begin{align} | :<math>\begin{align} | ||
\mathcal{Y}_2(\omega)&=\frac{1}{2\pi(2j)}\mathcal{X}(\omega)*[2\pi\delta(\omega-\omega_c)-2\pi\delta(\omega+\omega_c)] \\ | \mathcal{Y}_2(\omega)&=\frac{1}{2\pi(2j)}\mathcal{X}(\omega)*[2\pi\delta(\omega-\omega_c)-2\pi\delta(\omega+\omega_c)] \\ | ||
&=\frac{1}{2j}\mathcal{X}(\omega-\omega_c)-\frac{1}{2j}\mathcal{X}(\omega+\omega_c) | &=\frac{1}{2j}\mathcal{X}(\omega-\omega_c)-\frac{1}{2j}\mathcal{X}(\omega+\omega_c) | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Now, to insure that we can recover signal < | + | Now, to insure that we can recover signal <span class="texhtml">''x''(''t'')</span> we need to avoid having the two images of <span class="texhtml">''X''(ω)</span> overlap. Hence we need <span class="texhtml">ω<sub>''c''</sub> > ω<sub>''M''</sub></span>. But <span class="texhtml">ω<sub>''M''</sub> = 2000π / 2 = 1000π</span>. Hence in order for <span class="texhtml">''x''(''t'')</span> to be recoverable we need: |
| − | :< | + | :<span class="texhtml">ω<sub>''c''</sub> > 1000π</span> |
| − | d)In order to recover signal < | + | d) In order to recover signal <span class="texhtml">''x''(''t'')</span> we multiply <span class="texhtml">''y''<sub>2</sub>(''t'')</span> by <span class="texhtml">sin(ω<sub>''c''</sub>''t'')</span> first. The signal after multiplying with <span class="texhtml">sin(ω<sub>''c''</sub>''t'')</span> is: |
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 33: | Line 34: | ||
&=\sin^2(\omega_c t)x(t) \\ | &=\sin^2(\omega_c t)x(t) \\ | ||
&=\frac{1}{2}x(t)-\frac{1}{2}\cos(2\omega_c t)x(t) | &=\frac{1}{2}x(t)-\frac{1}{2}\cos(2\omega_c t)x(t) | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | Thus in order to recover < | + | Thus in order to recover <span class="texhtml">''x''(''t'')</span> we need to filter out the second term of <span class="texhtml">''r''(''t'')</span> and amplify the remainder by a factor of 2 (you may want to draw the FT of <span class="texhtml">''r''(''t'')</span> to verify this in the frequency domain). To achieve that, we pass <span class="texhtml">''r''(''t'')</span> through a low pass filter with a cut-off frequency <span class="texhtml">ω<sub>''c''''u''''t''</sub> = ω<sub>''M''</sub> = 1000π</span> and gain 2. The frequency response of this low pass filter is: |
:<math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | :<math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | ||
2, & \mbox{ for } |\omega|<1000\pi\\ | 2, & \mbox{ for } |\omega|<1000\pi\\ | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
| − | \end{array}\right. | + | \end{array}\right.</math> |
| − | </math> | + | |
| − | Note that the cut-off frequency of the low pass filter can actually be anywhere between < | + | Note that the cut-off frequency of the low pass filter can actually be anywhere between <span class="texhtml">ω<sub>''M''</sub></span> and <span class="texhtml">2ω<sub>''c''</sub> − ω<sub>''M''</sub></span>. |
| − | + | <br> | |
| − | a) The Fourier series coefficients of < | + | == Question 2 == |
| + | |||
| + | a) The Fourier series coefficients of <span class="texhtml">''c''(''t'')</span> are: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
a_k&=\frac{\sin(\frac{2\pi k 10^{-3}}{4\times 10^{-3}})}{\pi k} \\ | a_k&=\frac{\sin(\frac{2\pi k 10^{-3}}{4\times 10^{-3}})}{\pi k} \\ | ||
&=\frac{\sin{\frac{\pi k}{2}}}{\pi k} | &=\frac{\sin{\frac{\pi k}{2}}}{\pi k} | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| − | and using the synthesis equation of the Fourier series we get: | + | and using the synthesis equation of the Fourier series we get: |
:<math>c(t)=\sum_{k=-\infty}^{\infty} a_k e^{j\frac{2\pi k}{T}t}=\sum_{k=-\infty}^{\infty} a_k e^{j2000\pi kt}</math> | :<math>c(t)=\sum_{k=-\infty}^{\infty} a_k e^{j\frac{2\pi k}{T}t}=\sum_{k=-\infty}^{\infty} a_k e^{j2000\pi kt}</math> | ||
| − | Taking the FT of the latter sum, we get: | + | Taking the FT of the latter sum, we get: |
:<math>\mathcal{C}(\omega)=2\pi\sum_{k=-\infty}^{\infty}a_k \delta(\omega-2000\pi k)</math> | :<math>\mathcal{C}(\omega)=2\pi\sum_{k=-\infty}^{\infty}a_k \delta(\omega-2000\pi k)</math> | ||
| − | Now, let < | + | Now, let <span class="texhtml">''y''(''t'') = ''x''(''t'')''c''(''t'')</span>, then: |
<math>\begin{align} | <math>\begin{align} | ||
| Line 71: | Line 72: | ||
\end{align}</math> | \end{align}</math> | ||
| − | In order to recover < | + | In order to recover <span class="texhtml">''x''(''t'')</span> we need to avoid aliasing and hence <span class="texhtml">2000π > 2ω<sub>''M''</sub></span>. Then <span class="texhtml">ω<sub>''M''</sub> < 1000π</span>. |
| − | b) We need to find < | + | b) We need to find <span class="texhtml">''a''<sub>0</sub></span> since the image at DC is multiplied by it: |
:<math>a_0=\lim_{k\to 0}\frac{\sin{\frac{\pi k}{2}}}{\pi k}=\frac{\frac{\pi k}{2}}{\pi k}=\frac{1}{2}</math> | :<math>a_0=\lim_{k\to 0}\frac{\sin{\frac{\pi k}{2}}}{\pi k}=\frac{\frac{\pi k}{2}}{\pi k}=\frac{1}{2}</math> | ||
| − | Now, to recover < | + | Now, to recover <span class="texhtml">''x''(''t'')</span> we need to filter out the images other than the image at DC and and multiply it by <math>\frac{1}{a_0}=2</math>. Hence we use a low pass filter with the following frequency response: |
:<math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | :<math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | ||
2, & \mbox{ for } |\omega|<\omega_{M}\\ | 2, & \mbox{ for } |\omega|<\omega_{M}\\ | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
| − | \end{array}\right. | + | \end{array}\right.</math> |
| − | </math> | + | |
| − | Note that the cut-off frequency of the low pass filter can actually be anywhere between < | + | Note that the cut-off frequency of the low pass filter can actually be anywhere between <span class="texhtml">ω<sub>''M''</sub></span> and <span class="texhtml">2000π − ω<sub>''M''</sub></span>. |
| − | + | <br> | |
| − | + | ||
| − | + | ||
| − | + | == Question 3 == | |
| − | + | a) We can assume any illustrative shape for the spectrum of signal <span class="texhtml">''x''(''t'')</span> as long as it is band-limited between <span class="texhtml"> − ω<sub>''M''</sub></span> and <span class="texhtml">ω<sub>''M''</sub></span>. | |
| − | [[Image: | + | [[Image:301 sp2011 boutin hw10 figure1.jpg]] |
| − | + | Thus the spectrum of <span class="texhtml">''y''(''t'')</span> is: | |
| − | [[Image: | + | [[Image:301 sp2011 boutin hw10 figure2.jpg]] |
| − | + | b) A block diagram of the scrambler that can generate the signal <span class="texhtml">''y''(''t'')</span> can be: | |
| − | + | [[Image:301 sp2011 boutin hw10 figure3.jpg]] | |
| − | + | You can verify that by taking the FT of <span class="texhtml">2''x''(''t'')cos(ω<sub>''M''</sub>''t'')</span>. | |
| − | + | c) The following block diagram describes a descrambler which can recover signal <span class="texhtml">''x''(''t'')</span> from <span class="texhtml">''y''(''t'')</span>. | |
| − | + | ||
| + | [[Image:301 sp2011 boutin hw10 figure4.jpg]] | ||
| + | |||
| + | where <math>\mathcal{H}(\omega)=\left\{\begin{array}{ll} | ||
| + | 1, & \mbox{ for } |\omega|<\omega_M\\ | ||
0, & \mbox{ elsewhere} | 0, & \mbox{ elsewhere} | ||
| − | \end{array}\right. | + | \end{array}\right.</math>. |
| − | </math>. | + | |
| − | Note that <math>\mathcal{H}(\omega)</math> is the frequency response of a low pass filter with cut-off frequency equals to < | + | Note that <math>\mathcal{H}(\omega)</math> is the frequency response of a low pass filter with cut-off frequency equals to <span class="texhtml">ω<sub>''M''</sub></span>. |
| + | |||
| + | You can verify that the system in the above block diagram can recover signal <span class="texhtml">''x''(''t'')</span> by following the same reasoning of part d) in Question 1. | ||
| + | |||
| + | == Question 4 == | ||
| − | |||
a) | a) | ||
| Line 121: | Line 125: | ||
X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(t+3)e^{-st} dt \\ | X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(t+3)e^{-st} dt \\ | ||
&=\int_{-3}^{\infty}e^{-(5+s)t} dt \\ | &=\int_{-3}^{\infty}e^{-(5+s)t} dt \\ | ||
| − | &=-\frac{1}{s+5}e^{-(5+s)t}|^{\infty}_{-3} \\ | + | &=-\frac{1}{s+5}e^{-(5+s)t}\Bigg|^{\infty}_{-3} \\ |
&=\frac{e^{3(5+s)}}{s+5} | &=\frac{e^{3(5+s)}}{s+5} | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
| + | where the ROC is: | ||
| − | |||
:<math>\mathcal{R}e\{5+s\}>0</math> | :<math>\mathcal{R}e\{5+s\}>0</math> | ||
:<math>5+\mathcal{R}e\{s\}>0</math> | :<math>5+\mathcal{R}e\{s\}>0</math> | ||
| − | :<math>\mathcal{R}e\{s\}>-5</math> | + | :<math>\mathcal{R}e\{s\}>-5</math> |
| − | b) | + | <span style="color:red"> This is an example where the ROC appears "like magic" at the end. Four points should be taken off for this. In order to get full credit, you must specify at which point the equality fails to hold in your computation of the Fourier transform. For example, like this: </span> |
| + | |||
| + | <math>\begin{align} | ||
| + | X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(t+3)e^{-st} dt \\ | ||
| + | &=\int_{-3}^{\infty}e^{-(5+s)t} dt \\ | ||
| + | &=-\frac{1}{s+5}e^{-(5+s)t}\Bigg|^{\infty}_{-3} \\ | ||
| + | &=\left\{ | ||
| + | \begin{array}{ll} | ||
| + | \frac{e^{3(5+s)}}{s+5},& \text{ if } \mathcal{R}e\{s\}>-5\\ | ||
| + | diverges, & \text{ else.} | ||
| + | \end{array} | ||
| + | \right. | ||
| + | \end{align}</math> | ||
| + | |||
| + | b) | ||
<math>\begin{align} | <math>\begin{align} | ||
X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(-t+5)e^{-st} dt \\ | X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(-t+5)e^{-st} dt \\ | ||
&=\int_{-\infty}^{5}e^{-(5+s)t} dt \\ | &=\int_{-\infty}^{5}e^{-(5+s)t} dt \\ | ||
| − | &=-\frac{1}{s+5}e^{-(5+s)t}|_{-\infty}^{5} \\ | + | &=-\frac{1}{s+5}e^{-(5+s)t}\Bigg|_{-\infty}^{5} \\ |
| − | &=-\frac{e^{-5(5+s)}}{s+5} | + | &=\left\{ |
| − | \end{ | + | \begin{array}{ll} |
| − | </math> | + | -\frac{e^{-5(5+s)}}{s+5}& \text{ if } \mathcal{R}e\{s\}<-5\\ |
| + | diverges, & \text{ else.} | ||
| + | \end{array} | ||
| + | \right. | ||
| + | \end{align}</math> | ||
| − | + | <br> c) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <br> <math>\begin{align} | |
| − | + | ||
| − | + | ||
| − | <math>\begin{align} | + | |
X(s)&=\int_{-\infty}^{\infty}e^{-5t}[u(t)-u(t-3)]e^{-st} dt \\ | X(s)&=\int_{-\infty}^{\infty}e^{-5t}[u(t)-u(t-3)]e^{-st} dt \\ | ||
&=\int_{0}^{3}e^{-(5+s)t} dt \\ | &=\int_{0}^{3}e^{-(5+s)t} dt \\ | ||
&=-\frac{1}{s+5}[e^{-3(5+s)}-1]\\ | &=-\frac{1}{s+5}[e^{-3(5+s)}-1]\\ | ||
&=\frac{1}{s+5}-\frac{e^{-3(5+s)}}{s+5} | &=\frac{1}{s+5}-\frac{e^{-3(5+s)}}{s+5} | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | |
where we did not need to constraint our result to a ROC (which is expected since the signal has finite duration). | where we did not need to constraint our result to a ROC (which is expected since the signal has finite duration). | ||
| − | d) | + | d) |
<math>\begin{align} | <math>\begin{align} | ||
X(s)&=\int_{-\infty}^{\infty}e^{-2|t|}e^{-st}dt \\ | X(s)&=\int_{-\infty}^{\infty}e^{-2|t|}e^{-st}dt \\ | ||
| − | &=\int_{-\infty}^{0}e^{2t}e^{-st}dt + \int_{0}^{\infty}e^ | + | &=\int_{-\infty}^{0}e^{2t}e^{-st}dt + \int_{0}^{\infty}e^{-2t}e^{-st}dt \\ |
| − | &=\int_{-\infty}^{0}e^{(2-s)t}dt + \int_{0}^{\infty}e^ | + | &=\int_{-\infty}^{0}e^{(2-s)t}dt + \int_{0}^{\infty}e^{-(2+s)t}dt \\ |
| − | &=\frac{1}{2-s}e^{(2-s)t}|^{0}_{-\infty}-\frac{1}{2+s}e^{-(2+s)t}|_{0}^{\infty} \\ | + | &=\frac{1}{2-s}e^{(2-s)t}\Bigg|^{0}_{-\infty}-\frac{1}{2+s}e^{-(2+s)t}\Bigg|_{0}^{\infty} |
| − | &=\frac{1}{2-s}+\frac{1}{2+s} | + | \end{align}</math> |
| − | \end{align} | + | |
| − | </math> | + | Now consider the first term: |
| + | |||
| + | <math>\begin{align} | ||
| + | \frac{1}{2-s}e^{(2-s)t}\Bigg|^{0}_{-\infty} &= | ||
| + | \left\{ | ||
| + | \begin{array}{ll} | ||
| + | \frac{1}{2-s} & \text{ if } \mathcal{R}e\{s\}<2\\ | ||
| + | diverges, & \text{ else.} | ||
| + | \end{array} | ||
| + | \right. | ||
| + | \end{align}</math> | ||
| + | |||
| + | So the ROC for this first term is <math>\mathcal{R}e\{s\}<2</math>. | ||
| + | <br><br> | ||
| + | <font color="blue">QUESTION: I understand that there is a pole at 2, but how do you know which direction the ROC goes (> or <)?</font><br><br> | ||
| + | |||
| + | |||
| + | Now consider the second term: | ||
| + | |||
| + | <math>\begin{align} | ||
| + | -\frac{1}{2+s}e^{-(2+s)t}\Bigg|_{0}^{\infty}&= | ||
| + | \left\{ | ||
| + | \begin{array}{ll} | ||
| + | \frac{1}{2+s} & \text{ if } \mathcal{R}e\{s\}>-2\\ | ||
| + | diverges, & \text{ else.} | ||
| + | \end{array} | ||
| + | \right. | ||
| + | \end{align}</math> | ||
| + | |||
| + | So the ROC for this second term is <math>\mathcal{R}e\{s\}>-2</math>. | ||
| + | |||
| + | Thus the ROC for the sum of both terms is the intersection of those two constraints, and hence the ROC is <math>-2<\mathcal{R}e\{s\}<2</math>. | ||
| + | |||
| + | <br> | ||
| − | + | == Question 5 == | |
| − | + | Since the Laplace transform of <span class="texhtml">''x''(''t'')</span> has exactly two poles at <span class="texhtml">''s'' = − 1</span> and <span class="texhtml">''s'' = − 3</span>, then the ROC could be any of the following three: | |
| − | Since the Laplace transform of < | + | |
:<math>\mathcal{R}e\{s\}<-1</math> | :<math>\mathcal{R}e\{s\}<-1</math> | ||
| Line 179: | Line 226: | ||
:<math>-3<\mathcal{R}e\{s\}<-1</math> | :<math>-3<\mathcal{R}e\{s\}<-1</math> | ||
| − | But it is given that the FT of < | + | But it is given that the FT of <span class="texhtml">''e''<sup>2''t''</sup>''x''(''t'')</span> converges and hence <span class="texhtml">''s'' = − 2</span> belongs to the ROC of the Laplace transform of <span class="texhtml">''x''(''t'')</span>. |
| − | Hence the ROC is <math | + | Hence the ROC is <math>-3<\mathcal{R}e\{s\}<-1</math>. |
| − | Since the ROC is <math | + | Since the ROC is <math>-3<\mathcal{R}e\{s\}<-1</math>, we deduce that the given signal is a sum of a right-sided signal and a left-sided signal. Thus, <span class="texhtml">''x''(''t'')</span> should be a two-sided signal. |
| − | Hence: | + | Hence: |
| − | a) No | + | a) No |
| − | b) No | + | b) No |
| − | + | ||
| − | + | ||
| − | + | c) Yes | |
| − | + | <br> | |
| − | First we compute the roots of the denominator, and then we get: | + | === Can you explain how you got s = -2 in more detail? I keep getting that the FT of exp(2t)x(t) = X(jw-2), which makes me think, for s = jw, X(s-2) --> s = 2. === |
| + | |||
| + | :<span style="color:blue">TA's comment: Since the FT of <math>e^{2t}x(t)</math> converges then the following integral converges: | ||
| + | :<math>\color{blue}\int_{-\infty}^{\infty}e^{2t}x(t)e^{-j\omega t}dt=\int_{-\infty}^{\infty}x(t)e^{-(-2+j\omega)t}dt</math></span> | ||
| + | |||
| + | :<span style="color:blue">Comparing the above integral with the definition of the Laplace transform we notice that it is <math>X(s)</math> but with <math class="inline">\color{blue}\mathcal{R}e\{s\}=-2</math> and hence the Laplace transform of <math>x(t)</math> converges for all s with <math class="inline">\color{blue}\mathcal{R}e\{s\}=-2</math>. | ||
| + | |||
| + | </span> | ||
| + | |||
| + | |||
| + | |||
| + | == Question 6 == | ||
| + | |||
| + | In order to find the inverse Laplace transform of <span class="texhtml">''X''(''s'')</span>, we need to find its partial fraction expansion. | ||
| + | |||
| + | First we compute the roots of the denominator, and then we get: | ||
:<math>X(s)=\frac{2(s+2)}{s^2+7s+12}=\frac{2(s+2)}{(s+3)(s+4)}</math> | :<math>X(s)=\frac{2(s+2)}{s^2+7s+12}=\frac{2(s+2)}{(s+3)(s+4)}</math> | ||
| − | Now we write: | + | Now we write: |
:<math>X(s)=\frac{A}{s+3}+\frac{B}{s+4}</math> | :<math>X(s)=\frac{A}{s+3}+\frac{B}{s+4}</math> | ||
| − | Multiplying both sides by < | + | Multiplying both sides by <span class="texhtml">(''s'' + 3)(''s'' + 4)</span> and simplifying, we get: |
| − | :< | + | :<span class="texhtml">2''s'' + 4 = (''A'' + ''B'')''s'' + 4''A'' + 3''B''</span> |
| − | Comparing and solving, we have that: < | + | Comparing and solving, we have that: <span class="texhtml">''A'' = − 2</span> and <span class="texhtml">''B'' = 4</span>. |
| − | Thus, | + | Thus, |
:<math>X(s)=-\frac{2}{s+3}+\frac{4}{s+4}</math> | :<math>X(s)=-\frac{2}{s+3}+\frac{4}{s+4}</math> | ||
| − | Now since the ROC is <math | + | Now since the ROC is <math>\mathcal{R}e\{s\}>-3</math>, then <span class="texhtml">''x''(''t'')</span> should be a right sided signal or equivalently the sum of right sided signals. Hence, |
| + | |||
| + | :<span class="texhtml">''x''(''t'') = [ − 2''e''<sup> − 3''t''</sup> + 4''e''<sup> − 4''t''</sup>]''u''(''t'')</span> | ||
| − | |||
---- | ---- | ||
| − | [[HW10 ECE301 Spring2011 Prof Boutin| HW10]] | + | |
| + | [[HW10 ECE301 Spring2011 Prof Boutin|HW10]] | ||
[[2011 Spring ECE 301 Boutin|Back to 2011 Spring ECE 301 Boutin]] | [[2011 Spring ECE 301 Boutin|Back to 2011 Spring ECE 301 Boutin]] | ||
[[Category:2011_Spring_ECE_301_Boutin]] | [[Category:2011_Spring_ECE_301_Boutin]] | ||
Latest revision as of 04:58, 22 April 2011
Homework 10 Solutions, ECE301 Spring 2011 Prof. Boutin
Students should feel free to make comments/corrections or ask questions directly on this page.
Question 1
a) We can write
- $ y_1(t)=e^{j \theta_c}x(t)e^{j\omega_c t} $
Notice that this is exactly as modulating by $ e^{j\omega_c t} $ but now we are multiplying with a complex exponential independent of t (phase shift). We can recover the signal x(t) for any ωc, and hence there are no conditions put on ωc.
b) In order to recover signal x(t), we multiply y1(t) by $ e^{-j(\omega_c t+\theta_c)} $.
c) We can write
- $ y_2(t)=x(t)\left(\frac{e^{j\omega_c t}-e^{-j\omega_c t}}{2j}\right) $
Taking the FT of y2(t), we get:
- $ \begin{align} \mathcal{Y}_2(\omega)&=\frac{1}{2\pi(2j)}\mathcal{X}(\omega)*[2\pi\delta(\omega-\omega_c)-2\pi\delta(\omega+\omega_c)] \\ &=\frac{1}{2j}\mathcal{X}(\omega-\omega_c)-\frac{1}{2j}\mathcal{X}(\omega+\omega_c) \end{align} $
Now, to insure that we can recover signal x(t) we need to avoid having the two images of X(ω) overlap. Hence we need ωc > ωM. But ωM = 2000π / 2 = 1000π. Hence in order for x(t) to be recoverable we need:
- ωc > 1000π
d) In order to recover signal x(t) we multiply y2(t) by sin(ωct) first. The signal after multiplying with sin(ωct) is:
- $ \begin{align} r(t)&=y_2(t)\sin(\omega_c t) \\ &=\sin^2(\omega_c t)x(t) \\ &=\frac{1}{2}x(t)-\frac{1}{2}\cos(2\omega_c t)x(t) \end{align} $
Thus in order to recover x(t) we need to filter out the second term of r(t) and amplify the remainder by a factor of 2 (you may want to draw the FT of r(t) to verify this in the frequency domain). To achieve that, we pass r(t) through a low pass filter with a cut-off frequency ωc'u't = ωM = 1000π and gain 2. The frequency response of this low pass filter is:
- $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} 2, & \mbox{ for } |\omega|<1000\pi\\ 0, & \mbox{ elsewhere} \end{array}\right. $
Note that the cut-off frequency of the low pass filter can actually be anywhere between ωM and 2ωc − ωM.
Question 2
a) The Fourier series coefficients of c(t) are:
- $ \begin{align} a_k&=\frac{\sin(\frac{2\pi k 10^{-3}}{4\times 10^{-3}})}{\pi k} \\ &=\frac{\sin{\frac{\pi k}{2}}}{\pi k} \end{align} $
and using the synthesis equation of the Fourier series we get:
- $ c(t)=\sum_{k=-\infty}^{\infty} a_k e^{j\frac{2\pi k}{T}t}=\sum_{k=-\infty}^{\infty} a_k e^{j2000\pi kt} $
Taking the FT of the latter sum, we get:
- $ \mathcal{C}(\omega)=2\pi\sum_{k=-\infty}^{\infty}a_k \delta(\omega-2000\pi k) $
Now, let y(t) = x(t)c(t), then:
$ \begin{align} \mathcal{Y}(\omega)&=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{C}(\omega) \\ &=\frac{1}{2\pi}\mathcal{X}(\omega)*2\pi\sum_{k=-\infty}^{\infty}a_k \delta(\omega-2000\pi k) \\ &=\sum_{k=-\infty}^{\infty}a_k \mathcal{X}(\omega-2000\pi k) \end{align} $
In order to recover x(t) we need to avoid aliasing and hence 2000π > 2ωM. Then ωM < 1000π.
b) We need to find a0 since the image at DC is multiplied by it:
- $ a_0=\lim_{k\to 0}\frac{\sin{\frac{\pi k}{2}}}{\pi k}=\frac{\frac{\pi k}{2}}{\pi k}=\frac{1}{2} $
Now, to recover x(t) we need to filter out the images other than the image at DC and and multiply it by $ \frac{1}{a_0}=2 $. Hence we use a low pass filter with the following frequency response:
- $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} 2, & \mbox{ for } |\omega|<\omega_{M}\\ 0, & \mbox{ elsewhere} \end{array}\right. $
Note that the cut-off frequency of the low pass filter can actually be anywhere between ωM and 2000π − ωM.
Question 3
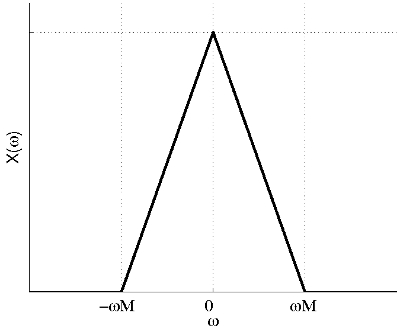
a) We can assume any illustrative shape for the spectrum of signal x(t) as long as it is band-limited between − ωM and ωM.
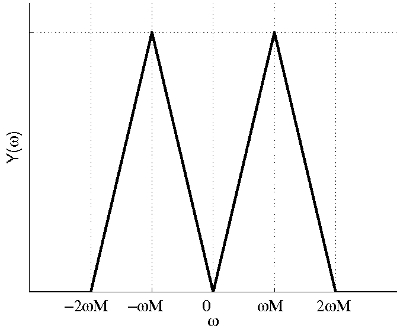
Thus the spectrum of y(t) is:
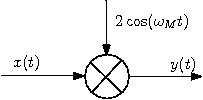
b) A block diagram of the scrambler that can generate the signal y(t) can be:
You can verify that by taking the FT of 2x(t)cos(ωMt).
c) The following block diagram describes a descrambler which can recover signal x(t) from y(t).
where $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} 1, & \mbox{ for } |\omega|<\omega_M\\ 0, & \mbox{ elsewhere} \end{array}\right. $.
Note that $ \mathcal{H}(\omega) $ is the frequency response of a low pass filter with cut-off frequency equals to ωM.
You can verify that the system in the above block diagram can recover signal x(t) by following the same reasoning of part d) in Question 1.
Question 4
a)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(t+3)e^{-st} dt \\ &=\int_{-3}^{\infty}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}e^{-(5+s)t}\Bigg|^{\infty}_{-3} \\ &=\frac{e^{3(5+s)}}{s+5} \end{align} $
where the ROC is:
- $ \mathcal{R}e\{5+s\}>0 $
- $ 5+\mathcal{R}e\{s\}>0 $
- $ \mathcal{R}e\{s\}>-5 $
This is an example where the ROC appears "like magic" at the end. Four points should be taken off for this. In order to get full credit, you must specify at which point the equality fails to hold in your computation of the Fourier transform. For example, like this:
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(t+3)e^{-st} dt \\ &=\int_{-3}^{\infty}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}e^{-(5+s)t}\Bigg|^{\infty}_{-3} \\ &=\left\{ \begin{array}{ll} \frac{e^{3(5+s)}}{s+5},& \text{ if } \mathcal{R}e\{s\}>-5\\ diverges, & \text{ else.} \end{array} \right. \end{align} $
b)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}u(-t+5)e^{-st} dt \\ &=\int_{-\infty}^{5}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}e^{-(5+s)t}\Bigg|_{-\infty}^{5} \\ &=\left\{ \begin{array}{ll} -\frac{e^{-5(5+s)}}{s+5}& \text{ if } \mathcal{R}e\{s\}<-5\\ diverges, & \text{ else.} \end{array} \right. \end{align} $
c)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-5t}[u(t)-u(t-3)]e^{-st} dt \\ &=\int_{0}^{3}e^{-(5+s)t} dt \\ &=-\frac{1}{s+5}[e^{-3(5+s)}-1]\\ &=\frac{1}{s+5}-\frac{e^{-3(5+s)}}{s+5} \end{align} $
where we did not need to constraint our result to a ROC (which is expected since the signal has finite duration).
d)
$ \begin{align} X(s)&=\int_{-\infty}^{\infty}e^{-2|t|}e^{-st}dt \\ &=\int_{-\infty}^{0}e^{2t}e^{-st}dt + \int_{0}^{\infty}e^{-2t}e^{-st}dt \\ &=\int_{-\infty}^{0}e^{(2-s)t}dt + \int_{0}^{\infty}e^{-(2+s)t}dt \\ &=\frac{1}{2-s}e^{(2-s)t}\Bigg|^{0}_{-\infty}-\frac{1}{2+s}e^{-(2+s)t}\Bigg|_{0}^{\infty} \end{align} $
Now consider the first term:
$ \begin{align} \frac{1}{2-s}e^{(2-s)t}\Bigg|^{0}_{-\infty} &= \left\{ \begin{array}{ll} \frac{1}{2-s} & \text{ if } \mathcal{R}e\{s\}<2\\ diverges, & \text{ else.} \end{array} \right. \end{align} $
So the ROC for this first term is $ \mathcal{R}e\{s\}<2 $.
QUESTION: I understand that there is a pole at 2, but how do you know which direction the ROC goes (> or <)?
Now consider the second term:
$ \begin{align} -\frac{1}{2+s}e^{-(2+s)t}\Bigg|_{0}^{\infty}&= \left\{ \begin{array}{ll} \frac{1}{2+s} & \text{ if } \mathcal{R}e\{s\}>-2\\ diverges, & \text{ else.} \end{array} \right. \end{align} $
So the ROC for this second term is $ \mathcal{R}e\{s\}>-2 $.
Thus the ROC for the sum of both terms is the intersection of those two constraints, and hence the ROC is $ -2<\mathcal{R}e\{s\}<2 $.
Question 5
Since the Laplace transform of x(t) has exactly two poles at s = − 1 and s = − 3, then the ROC could be any of the following three:
- $ \mathcal{R}e\{s\}<-1 $
- $ \mathcal{R}e\{s\}<-3 $
- $ -3<\mathcal{R}e\{s\}<-1 $
But it is given that the FT of e2tx(t) converges and hence s = − 2 belongs to the ROC of the Laplace transform of x(t).
Hence the ROC is $ -3<\mathcal{R}e\{s\}<-1 $.
Since the ROC is $ -3<\mathcal{R}e\{s\}<-1 $, we deduce that the given signal is a sum of a right-sided signal and a left-sided signal. Thus, x(t) should be a two-sided signal.
Hence:
a) No
b) No
c) Yes
Can you explain how you got s = -2 in more detail? I keep getting that the FT of exp(2t)x(t) = X(jw-2), which makes me think, for s = jw, X(s-2) --> s = 2.
- TA's comment: Since the FT of $ e^{2t}x(t) $ converges then the following integral converges:
- $ \color{blue}\int_{-\infty}^{\infty}e^{2t}x(t)e^{-j\omega t}dt=\int_{-\infty}^{\infty}x(t)e^{-(-2+j\omega)t}dt $
- Comparing the above integral with the definition of the Laplace transform we notice that it is $ X(s) $ but with $ \color{blue}\mathcal{R}e\{s\}=-2 $ and hence the Laplace transform of $ x(t) $ converges for all s with $ \color{blue}\mathcal{R}e\{s\}=-2 $.
Question 6
In order to find the inverse Laplace transform of X(s), we need to find its partial fraction expansion.
First we compute the roots of the denominator, and then we get:
- $ X(s)=\frac{2(s+2)}{s^2+7s+12}=\frac{2(s+2)}{(s+3)(s+4)} $
Now we write:
- $ X(s)=\frac{A}{s+3}+\frac{B}{s+4} $
Multiplying both sides by (s + 3)(s + 4) and simplifying, we get:
- 2s + 4 = (A + B)s + 4A + 3B
Comparing and solving, we have that: A = − 2 and B = 4.
Thus,
- $ X(s)=-\frac{2}{s+3}+\frac{4}{s+4} $
Now since the ROC is $ \mathcal{R}e\{s\}>-3 $, then x(t) should be a right sided signal or equivalently the sum of right sided signals. Hence,
- x(t) = [ − 2e − 3t + 4e − 4t]u(t)