| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | = 6 Finals = | |
| − | '''Example (Important because it was dealt in the class)''' | + | '''Example (Important because it was dealt in the class)''' |
| − | Let <math>\mathbf{X}\left(t\right)</math> | + | Let <math class="inline">\mathbf{X}\left(t\right)</math> be a WSS random process with PSD <math class="inline">S_{\mathbf{XX}}\left(\omega\right)</math> and let <math class="inline">\mathbf{Y}\left(t\right)</math> be the “smoothed” random process given by <math class="inline">\mathbf{Y}\left(t\right)=\frac{1}{2T}\int_{t-T}^{t+T}\mathbf{X}\left(\alpha\right)d\alpha.</math> |
| − | <br> | + | <br>This can be represented by a LTI system |
| − | This can be represented by a LTI system | + | |
| − | [[Image: | + | [[Image:Pasted22.png]] |
| + | |||
| − | with impulse response <math>h\left(t\right)=\frac{1}{2T}\mathbf{1}_{\left[-T,T\right]}\left(t\right)</math>. | + | with impulse response <math class="inline">h\left(t\right)=\frac{1}{2T}\mathbf{1}_{\left[-T,T\right]}\left(t\right)</math>. What is the PSD <math class="inline">S_{\mathbf{YY}}\left(\omega\right)</math> of <math class="inline">\mathbf{Y}\left(t\right)</math> ? |
| − | '''Solution''' | + | '''Solution''' |
| − | <math>H\left(\omega\right)=\int_{-\infty}^{\infty}h\left(t\right)e^{-i\omega t}dt=\int_{-\infty}^{\infty}\frac{1}{2T}\mathbf{1}_{\left[-T,T\right]}\left(t\right)e^{-i\omega t}dt=\frac{1}{2T}\int_{-T}^{T}e^{-i\omega t}dt</math><math>=\left.\frac{1}{2T}\frac{e^{-i\omega t}}{-i\omega}\right|_{-T}^{T}=\frac{1}{2T}\frac{e^{-i\omega T}-e^{i\omega T}}{-i\omega}=\frac{1}{2T}\frac{\left(\cos\omega T-i\sin\omega T\right)-\left(\cos\omega T+i\sin\omega T\right)}{-i\omega}</math>< | + | <math class="inline">H\left(\omega\right)=\int_{-\infty}^{\infty}h\left(t\right)e^{-i\omega t}dt=\int_{-\infty}^{\infty}\frac{1}{2T}\mathbf{1}_{\left[-T,T\right]}\left(t\right)e^{-i\omega t}dt=\frac{1}{2T}\int_{-T}^{T}e^{-i\omega t}dt</math><math class="inline">=\left.\frac{1}{2T}\frac{e^{-i\omega t}}{-i\omega}\right|_{-T}^{T}=\frac{1}{2T}\frac{e^{-i\omega T}-e^{i\omega T}}{-i\omega}=\frac{1}{2T}\frac{\left(\cos\omega T-i\sin\omega T\right)-\left(\cos\omega T+i\sin\omega T\right)}{-i\omega}</math><span class="texhtml"> </span> |
| − | + | {| | |
| + | |- style="vertical-align: bottom; text-align: center" | ||
| + | | | ||
| + | | 1 | ||
| + | | 2sinω''T'' | ||
| + | | | ||
| + | | sinω''T'' | ||
| + | | | ||
| + | |- style="text-align: center" | ||
| + | | = | ||
| + | | | ||
| + | ---- | ||
| − | + | | | |
| + | ---- | ||
| − | + | | = | |
| + | | | ||
| + | ---- | ||
| − | + | | . | |
| + | |- style="vertical-align: top; text-align: center" | ||
| + | | | ||
| + | | 2''T'' | ||
| + | | ω | ||
| + | | | ||
| + | | ω''T'' | ||
| + | | | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | <math class="inline">S_{\mathbf{YY}}\left(\omega\right)=S_{\mathbf{XX}}\left(\omega\right)\left|H\left(\omega\right)\right|^{2}=S_{\mathbf{XX}}\left(\omega\right)\left|\frac{\sin\omega T}{\omega T}\right|^{2}.</math> | |
| − | <math> | + | Note that <math class="inline">h\left(t\right)</math> acts as a crude low-pass filter that attenuates high-frequency power. |
| − | + | [[Image:Pasted23.png]] | |
| − | + | Example (True or False) | |
| − | + | Let <math class="inline">\mathbf{X}\left(t\right)</math> and <math class="inline">\mathbf{Y}\left(t\right)</math> be two zero-mean statistically independent, jointly wide-sense stationary random processes. Then the cross-correlation function <math class="inline">R_{\mathbf{XY}}\left(\tau\right)=0</math> . | |
| − | ''False.'' | + | '''Solution''' |
| + | |||
| + | ''True.'' | ||
| + | |||
| + | <math class="inline">R_{\mathbf{XY}}\left(t_{1},t_{2}\right)=E\left[\mathbf{X}\left(t_{1}\right)\mathbf{Y}^{*}\left(t_{2}\right)\right]=E\left[\mathbf{X}\left(t_{1}\right)\right]E\left[\mathbf{Y}^{*}\left(t_{2}\right)\right]=0\cdot0=0.</math> | ||
| + | |||
| + | '''Example (True or False)''' | ||
| + | |||
| + | The cross-correlation function <math class="inline">R_{\mathbf{XY}}\left(\tau\right)</math> of two real, jointly wide-sense stationary random process <math class="inline">\mathbf{X}\left(t\right)</math> and <math class="inline">\mathbf{Y}\left(t\right)</math> is an even function of <span class="texhtml">τ</span> . | ||
| + | |||
| + | '''Solution''' | ||
| + | |||
| + | ''False.'' | ||
| + | |||
| + | *[[ECE 600 Finals MRB 1992 Final|1992 Final]] | ||
| + | *[[ECE 600 Finals MRB 1994 Final|1994 Final]] | ||
| + | *[[ECE 600 Finals MRB 2004 Final|2004 Spring Final]] | ||
| + | |||
| + | ---- | ||
| + | [[ECE600|Back to ECE600]] | ||
Latest revision as of 06:16, 1 December 2010
6 Finals
Example (Important because it was dealt in the class)
Let $ \mathbf{X}\left(t\right) $ be a WSS random process with PSD $ S_{\mathbf{XX}}\left(\omega\right) $ and let $ \mathbf{Y}\left(t\right) $ be the “smoothed” random process given by $ \mathbf{Y}\left(t\right)=\frac{1}{2T}\int_{t-T}^{t+T}\mathbf{X}\left(\alpha\right)d\alpha. $
This can be represented by a LTI system
with impulse response $ h\left(t\right)=\frac{1}{2T}\mathbf{1}_{\left[-T,T\right]}\left(t\right) $. What is the PSD $ S_{\mathbf{YY}}\left(\omega\right) $ of $ \mathbf{Y}\left(t\right) $ ?
Solution
$ H\left(\omega\right)=\int_{-\infty}^{\infty}h\left(t\right)e^{-i\omega t}dt=\int_{-\infty}^{\infty}\frac{1}{2T}\mathbf{1}_{\left[-T,T\right]}\left(t\right)e^{-i\omega t}dt=\frac{1}{2T}\int_{-T}^{T}e^{-i\omega t}dt $$ =\left.\frac{1}{2T}\frac{e^{-i\omega t}}{-i\omega}\right|_{-T}^{T}=\frac{1}{2T}\frac{e^{-i\omega T}-e^{i\omega T}}{-i\omega}=\frac{1}{2T}\frac{\left(\cos\omega T-i\sin\omega T\right)-\left(\cos\omega T+i\sin\omega T\right)}{-i\omega} $
| 1 | 2sinωT | sinωT | |||
| = |
|
|
= |
|
. |
| 2T | ω | ωT |
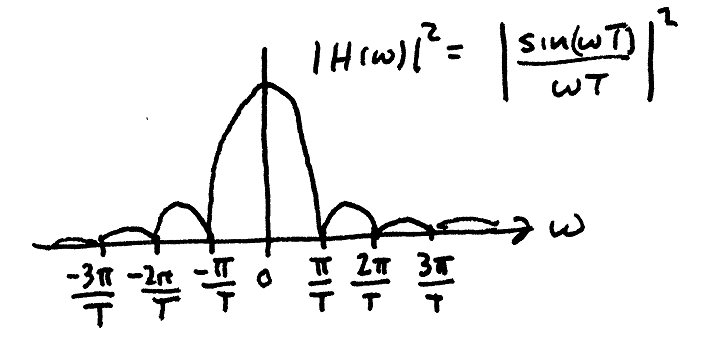
$ S_{\mathbf{YY}}\left(\omega\right)=S_{\mathbf{XX}}\left(\omega\right)\left|H\left(\omega\right)\right|^{2}=S_{\mathbf{XX}}\left(\omega\right)\left|\frac{\sin\omega T}{\omega T}\right|^{2}. $
Note that $ h\left(t\right) $ acts as a crude low-pass filter that attenuates high-frequency power.
Example (True or False)
Let $ \mathbf{X}\left(t\right) $ and $ \mathbf{Y}\left(t\right) $ be two zero-mean statistically independent, jointly wide-sense stationary random processes. Then the cross-correlation function $ R_{\mathbf{XY}}\left(\tau\right)=0 $ .
Solution
True.
$ R_{\mathbf{XY}}\left(t_{1},t_{2}\right)=E\left[\mathbf{X}\left(t_{1}\right)\mathbf{Y}^{*}\left(t_{2}\right)\right]=E\left[\mathbf{X}\left(t_{1}\right)\right]E\left[\mathbf{Y}^{*}\left(t_{2}\right)\right]=0\cdot0=0. $
Example (True or False)
The cross-correlation function $ R_{\mathbf{XY}}\left(\tau\right) $ of two real, jointly wide-sense stationary random process $ \mathbf{X}\left(t\right) $ and $ \mathbf{Y}\left(t\right) $ is an even function of τ .
Solution
False.