(New page: == Chebyshev inequality == Let <math>\mathbf{X}</math> be a random variable with mean <math>\mu</math> and variance <math>\sigma^{2}</math>. Then <math>\forall\epsilon>0</math> <math> ...) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | == Chebyshev inequality == | + | [[Category:random_variables]] |
| + | [[Category:ECE600]] | ||
| + | [[Category:Sangchun_Han]] | ||
| + | |||
| + | = Two Proofs of Chebyshev inequality= | ||
| + | by [[user:han84|Sangchun Han]], PhD student in [[ECE]] | ||
| + | ---- | ||
| + | == Question: Prove Chebyshev's inequality: == | ||
Let <math>\mathbf{X}</math> be a random variable with mean <math>\mu</math> and variance <math>\sigma^{2}</math>. Then <math>\forall\epsilon>0</math> | Let <math>\mathbf{X}</math> be a random variable with mean <math>\mu</math> and variance <math>\sigma^{2}</math>. Then <math>\forall\epsilon>0</math> | ||
| − | <math> | + | :<math> |
p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. | p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. | ||
</math> | </math> | ||
| − | + | ---- | |
| + | ==Answers== | ||
=== Proof 1 === | === Proof 1 === | ||
[[Image:ECE600_Note_Chebyshev_inequality1.jpg]] | [[Image:ECE600_Note_Chebyshev_inequality1.jpg]] | ||
| Line 39: | Line 47: | ||
\therefore p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. | \therefore p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. | ||
</math> | </math> | ||
| − | + | ---- | |
| + | ==Discussion== | ||
| + | ---- | ||
=== Proof 2 === | === Proof 2 === | ||
| Line 57: | Line 67: | ||
\therefore p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. | \therefore p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. | ||
</math> | </math> | ||
| + | ---- | ||
| + | ==Discussion== | ||
| + | ---- | ||
| + | [[ECE600|Back to ECE600]] | ||
| + | |||
| + | [[2010_Fall_ECE_600_Comer|Back to ECE 600, Fall 2010, Prof. Comer]] | ||
Latest revision as of 10:26, 16 November 2010
Contents
Two Proofs of Chebyshev inequality
by Sangchun Han, PhD student in ECE
Question: Prove Chebyshev's inequality:
Let $ \mathbf{X} $ be a random variable with mean $ \mu $ and variance $ \sigma^{2} $. Then $ \forall\epsilon>0 $
- $ p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. $
Answers
Proof 1
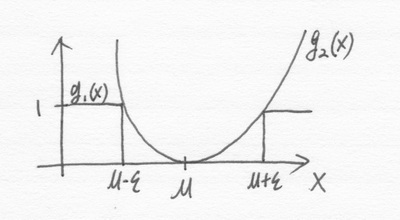
Let $ g_{1}\left(\mathbf{X}\right)=\mathbf{1}_{\left\{ r\in\mathbf{R}:\left|\mathbf{X}-\mu\right|\geq\epsilon\right\} }\left(\mathbf{X}\right) $ and $ g_{2}\left(\mathbf{X}\right)=\frac{\left(\mathbf{X}-\mu\right)^{2}}{\epsilon^{2}}. $
Let $ \phi\left(\mathbf{X}\right)=g_{2}\left(\mathbf{X}\right)-g_{1}\left(\mathbf{X}\right)\Longrightarrow\phi\left(\mathbf{X}\right)\geq0,\;\forall\mathbf{X}\in\mathbf{R}. $
$ E\left[\phi\left(\mathbf{X}\right)\right]=E\left[g_{2}\left(\mathbf{X}\right)-g_{1}\left(\mathbf{X}\right)\right]=E\left[g_{2}\left(\mathbf{X}\right)\right]-E\left[g_{1}\left(\mathbf{X}\right)\right]=\frac{\sigma^{2}}{\epsilon^{2}}-p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right) $ and $ E\left[\phi\left(\mathbf{X}\right)\right]\geq0. $
$ \because E\left[g_{2}\left(\mathbf{X}\right)\right]=E\left[\frac{\left(\mathbf{X}-\mu\right)^{2}}{\epsilon^{2}}\right]=\frac{1}{\epsilon^{2}}E\left[\left(\mathbf{X}-\mu\right)^{2}\right]=\frac{\sigma^{2}}{\epsilon^{2}}. $
$ \therefore p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. $
Discussion
Proof 2
$ E\left[\mathbf{X}\right]=\int_{0}^{\epsilon}xf_{\mathbf{X}}\left(x\right)dx+\int_{\epsilon}^{\infty}xf_{\mathbf{X}}\left(x\right)dx\geq\int_{\epsilon}^{\infty}xf_{\mathbf{X}}\left(x\right)dx\geq\int_{\epsilon}^{\infty}\epsilon f_{\mathbf{X}}\left(x\right)dx=\epsilon P\left(\left\{ \mathbf{X}\geq\epsilon\right\} \right). $
$ P\left(\left\{ \mathbf{X}\geq\epsilon\right\} \right)\leq\frac{E\left[\mathbf{X}\right]}{\epsilon}. $
$ P\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)=P\left(\left\{ \left(\mathbf{X}-\mu\right)^{2}\geq\epsilon^{2}\right\} \right)\leq\frac{E\left[\left(\mathbf{X}-\mu\right)^{2}\right]}{\epsilon^{2}}=\frac{\sigma^{2}}{\epsilon^{2}}. $
$ \therefore p\left(\left\{ \left|\mathbf{X}-\mu\right|\geq\epsilon\right\} \right)\leq\frac{\sigma^{2}}{\epsilon^{2}}. $