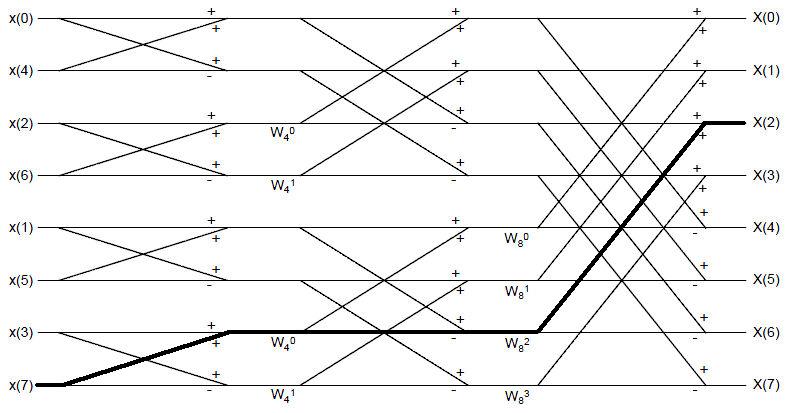
(New page: Image:Week8_Q3_FFT.jpg a) We decimate 3 times to compute DFT. The gain of one path equals to the product of gain of each decimate. According to the figure. <math>\text{ Gain }=(W_N^0...) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Week8 Quiz Question 3 Solution== | ||
| + | |||
[[Image:Week8_Q3_FFT.jpg]] | [[Image:Week8_Q3_FFT.jpg]] | ||
| Line 38: | Line 40: | ||
----------------------- | ----------------------- | ||
| − | [[ | + | [[ECE438_Week8_Quiz|Back to Quiz Pool]] |
Latest revision as of 16:27, 12 October 2010
Week8 Quiz Question 3 Solution
a) We decimate 3 times to compute DFT. The gain of one path equals to the product of gain of each decimate.
According to the figure. $ \text{ Gain }=(W_N^0)*(-1)*(W_N^2)=-W_N^2 $
b) Only one. In general, there is only one path between each input sample and each output sample.
c) $ x[0]\text{ to }X[2]\text{ : The gain is }1 $
$ x[1]\text{ to }X[2]\text{ : The gain is }W_N^2 $
$ x[2]\text{ to }X[2]\text{ : The gain is }-W_N^0=-1 $
$ x[3]\text{ to }X[2]\text{ : The gain is }-W_N^0 W_N^2=-W_N^2 $
$ x[4]\text{ to }X[2]\text{ : The gain is }W_N^0=1 $
$ x[5]\text{ to }X[2]\text{ : The gain is }W_N^0 W_N^2=W_N^2 $
$ x[6]\text{ to }X[2]\text{ : The gain is }-W_N^0 W_N^0=-1 $
$ x[7]\text{ to }X[2]\text{ : The gain is }-W_N^0 W_N^0 W_N^2=-W_N^2\text{, as in Part (a)} $
$ \text{Since }X[k]=\sum_{n=0}^{N-1}x[n]W_N^{nk} \text{, k=0,1,...,N-1} $
Now
$ \begin{align} X[2] &= \sum_{n=0}^7 x[n]W_8^{2n} \\ &= x[0]+x[1]W_8^2+x[2]W_8^4+x[3]W_8^6+x[4]W_8^8+x[5]W_8^10+x[6]W_8^12+x[7]W_8^14 \\ &= x[0]+x[1]W_8^2+x[2](-1)+x[3](-W_8^2)+x[4](1)+x[5]W_8^2+x[6](-1)+x[7](-W_8^2) \end{align} $
Thus, each input sample contributes the proper amount to the output DFT sample.