| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | =[[Hw3_ECE662Spring2010|Homework 3]] discussion, [[ECE662]], Spring 2010, [[user:mboutin|Prof. Boutin]]= | |
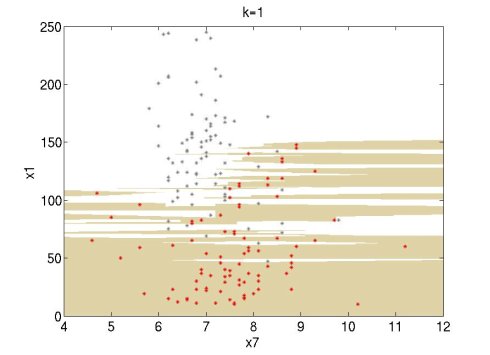
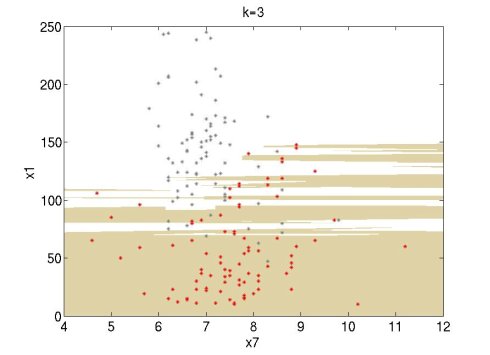
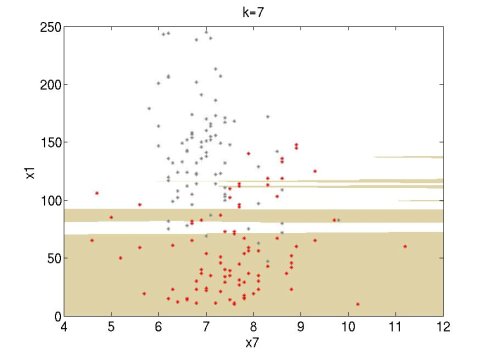
| − | I tried it and it works well. I did some experiments using the Wine data set of UCI (http://archive.ics.uci.edu/ml/datasets.html). I used attributes 1 and 7 of the red wine data set (red points) and the white wine data set (grey points). For this simple experiment, I used only the first 100 data points of each set. The following figures show the classification regions using k=1, 3, 7. The red wine region is brown and the white wine region is white. The regions are constructed using MATLAB's contourf function. | + | |
| + | I found a MATLAB [http://www.mathworks.com/matlabcentral/fileexchange/15562-k-nearest-neighbors function] for finding the k-nearest neighbors (kNN) within a set of points, which could be useful for homework 3. | ||
| + | |||
| + | I tried it and it works well. I did some experiments using the Wine data set of UCI (http://archive.ics.uci.edu/ml/datasets.html). I used attributes 1 and 7 of the red wine data set (red points) and the white wine data set (grey points). For this simple experiment, I used only the first 100 data points of each set. The following figures show the classification regions using k=1, 3, 7. The red wine region is brown and the white wine region is white. The regions are constructed using MATLAB's [http://www.mathworks.com/access/helpdesk/help/techdoc/ref/contourf.html contourf] function. | ||
[[Image:nn_k_1.jpg]] [[Image:nn_k_3.jpg]] [[Image:nn_k_7.jpg]] | [[Image:nn_k_1.jpg]] [[Image:nn_k_3.jpg]] [[Image:nn_k_7.jpg]] | ||
| + | |||
| + | --[[User:ilaguna|ilaguna]] 15:40, 7 April 2010 (UTC) | ||
| + | |||
| + | "Traveling Salesman Problem" (TSP) is one of the interesting applications of K-nearest neighbors (KNN) method. As you know, TSP is one of the most important problem in algorithm design area. KNN is a sub-optimal approach for this problem. You can find more info about it in this page http://en.wikipedia.org/wiki/Nearest_neighbour_algorithm and there is an interesting java applet in this webpage: http://www.wiley.com/college/mat/gilbert139343/java/java09_s.html. | ||
| + | |||
| + | Have fun,--[[User:Gmoayeri|Gmoayeri]] 20:24, 9 May 2010 (UTC) | ||
| + | |||
| + | |||
| + | =Non-parametric density estimation in R= | ||
| + | If you are using R for this HW then you might find these functions of interest for the non-parametric density estimation: | ||
| + | |||
| + | k-Nearest neighbors and nearest neighbor methods are implemented in these two functions: | ||
| + | |||
| + | knn, knn1 (Package "class"). | ||
| + | |||
| + | In this case you can directly enter your training data, classification of the training data and your test data and it will give you classification for all data. | ||
| + | (more details here: http://stat.ethz.ch/R-manual/R-patched/library/class/html/knn.html ) | ||
| + | |||
| + | |||
| + | I haven't found a method for data classification using Parzen window method, but you can use some packages for kernel density estimation of multivariate data. The best package I found is called "np" and you can estimate the density for a given training and sample data for example using this function: | ||
| + | |||
| + | npudens() | ||
| + | |||
| + | By default it uses the Gaussian kernel but you can specify which kernel to use using parameter "ckertype". The size of the kernel (size of the Parzen window) can be changed by modifying the bandwith of the kernel (parameter "bws") | ||
| + | (see: http://cran.r-project.org/web/packages/np/np.pdf ) | ||
| + | |||
| + | Hope that helps, | ||
| + | |||
| + | --[[User:ostava|ostava]] 20:35, 27 April 2010 (UTC) | ||
| + | |||
| + | ---- | ||
| + | [[2010_Spring_ECE_662_mboutin|back to ECE662, Spring 2010, Prof. Boutin]] | ||
Latest revision as of 15:24, 9 May 2010
Homework 3 discussion, ECE662, Spring 2010, Prof. Boutin
I found a MATLAB function for finding the k-nearest neighbors (kNN) within a set of points, which could be useful for homework 3.
I tried it and it works well. I did some experiments using the Wine data set of UCI (http://archive.ics.uci.edu/ml/datasets.html). I used attributes 1 and 7 of the red wine data set (red points) and the white wine data set (grey points). For this simple experiment, I used only the first 100 data points of each set. The following figures show the classification regions using k=1, 3, 7. The red wine region is brown and the white wine region is white. The regions are constructed using MATLAB's contourf function.
--ilaguna 15:40, 7 April 2010 (UTC)
"Traveling Salesman Problem" (TSP) is one of the interesting applications of K-nearest neighbors (KNN) method. As you know, TSP is one of the most important problem in algorithm design area. KNN is a sub-optimal approach for this problem. You can find more info about it in this page http://en.wikipedia.org/wiki/Nearest_neighbour_algorithm and there is an interesting java applet in this webpage: http://www.wiley.com/college/mat/gilbert139343/java/java09_s.html.
Have fun,--Gmoayeri 20:24, 9 May 2010 (UTC)
Non-parametric density estimation in R
If you are using R for this HW then you might find these functions of interest for the non-parametric density estimation:
k-Nearest neighbors and nearest neighbor methods are implemented in these two functions:
knn, knn1 (Package "class").
In this case you can directly enter your training data, classification of the training data and your test data and it will give you classification for all data. (more details here: http://stat.ethz.ch/R-manual/R-patched/library/class/html/knn.html )
I haven't found a method for data classification using Parzen window method, but you can use some packages for kernel density estimation of multivariate data. The best package I found is called "np" and you can estimate the density for a given training and sample data for example using this function:
npudens()
By default it uses the Gaussian kernel but you can specify which kernel to use using parameter "ckertype". The size of the kernel (size of the Parzen window) can be changed by modifying the bandwith of the kernel (parameter "bws") (see: http://cran.r-project.org/web/packages/np/np.pdf )
Hope that helps,
--ostava 20:35, 27 April 2010 (UTC)