| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | =The importance of eliminating aliasing= | ||
Aliasing is what occurs when a signal is not able to be completely reconstructed due to an insufficient sampling rate. This phenomenon may occur if the sampling frequency is below what is known as the Nyquist Frequency. The Nyquist Frequency can be expressed as: <math>F_n = F_s*2</math> where <math>F_s</math> is the highest frequency in the signal. | Aliasing is what occurs when a signal is not able to be completely reconstructed due to an insufficient sampling rate. This phenomenon may occur if the sampling frequency is below what is known as the Nyquist Frequency. The Nyquist Frequency can be expressed as: <math>F_n = F_s*2</math> where <math>F_s</math> is the highest frequency in the signal. | ||
| Line 18: | Line 19: | ||
[[Image:cossample100.jpg]] | [[Image:cossample100.jpg]] | ||
| − | |||
| − | |||
As you can see sampling the signal at over 100Hz there is no threat of aliasing, but let's see what happens when we sample at 75Hz. | As you can see sampling the signal at over 100Hz there is no threat of aliasing, but let's see what happens when we sample at 75Hz. | ||
| Line 34: | Line 33: | ||
The signal is the 2 deltas at <math>\omega=-4*\pi/3</math> and <math>\omega=4*\pi/3</math> | The signal is the 2 deltas at <math>\omega=-4*\pi/3</math> and <math>\omega=4*\pi/3</math> | ||
| − | However, that is not the fundamental frequency of <math>\omega=2*\pi/3</math> | + | However, that is not the fundamental frequency of <math>\omega=2*\pi/3</math> shown on the graph. |
| − | + | ||
| − | While sampling above the Nyquist Frequency will eliminate aliasing it is possible to sample below it and still not get aliasing | + | Note: |
| + | While sampling above the Nyquist Frequency will eliminate aliasing it is possible to sample below it and still not get aliasing. However this depends on the signal itself and is not recommended for general sampling. | ||
| + | ---- | ||
| + | [[ECE301|Back to ECE301]] | ||
| + | [[Category:aliasing]] | ||
Latest revision as of 07:24, 9 March 2011
The importance of eliminating aliasing
Aliasing is what occurs when a signal is not able to be completely reconstructed due to an insufficient sampling rate. This phenomenon may occur if the sampling frequency is below what is known as the Nyquist Frequency. The Nyquist Frequency can be expressed as: $ F_n = F_s*2 $ where $ F_s $ is the highest frequency in the signal.
To show some of the dangers of aliasing here are some examples.
Example 1: Say you have the signal $ x(t)= \cos(2*\Pi*50t) $
Then the Nyquist Frequency would be $ 2*50Hz = 100Hz $
If we sample at 200 Hz, the sampled signal would be
$ x[n] = x(nT)=x(\frac{n}{75})=\cos(\frac{2*\pi*50*n}{200}) $
with a transform of
$ \mathfrak{F}(\omega)=\sum_{n=-\infty}^{\infty}x[n]*e^{-jn\omega} $
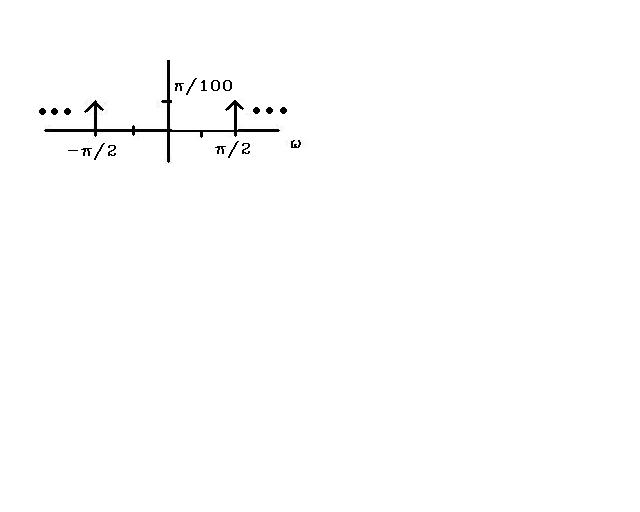
This would look like
As you can see sampling the signal at over 100Hz there is no threat of aliasing, but let's see what happens when we sample at 75Hz.
At 75Hz, $ T_s=\frac{1}{75}s $
Then, $ x[n] = x(nT)=x(\frac{n}{75})=\cos(\frac{2*\pi*50*n}{75}) $
$ \mathfrak{F}(\omega)=\sum_{n=-\infty}^{\infty}x[n]*e^{-jn\omega} $
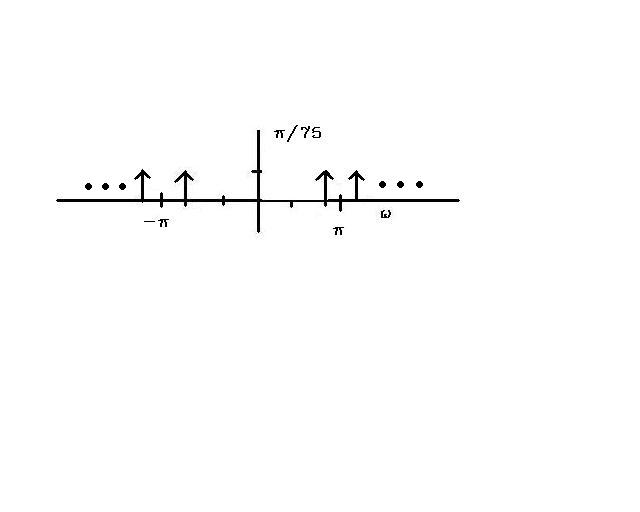
The transform will look something like
The signal is the 2 deltas at $ \omega=-4*\pi/3 $ and $ \omega=4*\pi/3 $ However, that is not the fundamental frequency of $ \omega=2*\pi/3 $ shown on the graph.
Note: While sampling above the Nyquist Frequency will eliminate aliasing it is possible to sample below it and still not get aliasing. However this depends on the signal itself and is not recommended for general sampling.