(New page: Image:xt.jpg Image:xst.jpg Image:x_d.jpg Image:x_f.jpg Image:xf_s.jpg Image:Xw.jpg Part I: how to convert CT signals to DT signals after sampling. Introduce variab...) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[ECE438_(BoutinFall2009)|Back to ECE438 course page]] | ||
| + | |||
| + | '''ECE 438 Fall Homework 3''' | ||
| + | |||
[[Image:xt.jpg]] | [[Image:xt.jpg]] | ||
[[Image:xst.jpg]] | [[Image:xst.jpg]] | ||
| Line 5: | Line 9: | ||
[[Image:xf_s.jpg]] | [[Image:xf_s.jpg]] | ||
[[Image:Xw.jpg]] | [[Image:Xw.jpg]] | ||
| − | |||
Part I: how to convert CT signals to DT signals after sampling. | Part I: how to convert CT signals to DT signals after sampling. | ||
Introduce variables: | Introduce variables: | ||
Latest revision as of 10:36, 23 September 2009
ECE 438 Fall Homework 3
Part I: how to convert CT signals to DT signals after sampling.
Introduce variables:
xc(t)=continuous time signal
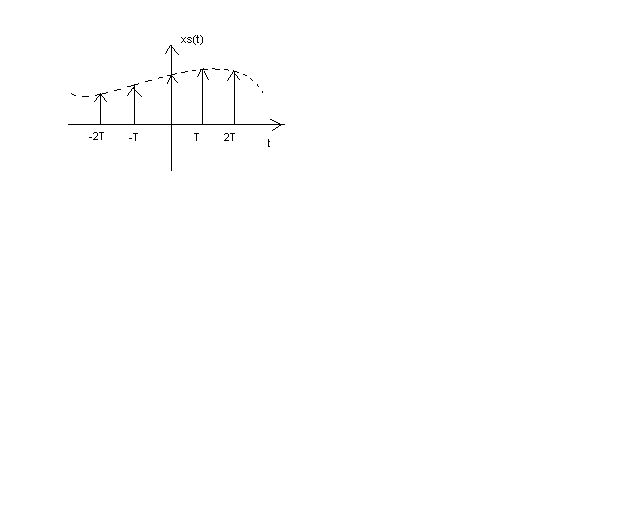
xs(t)=signals after sampling
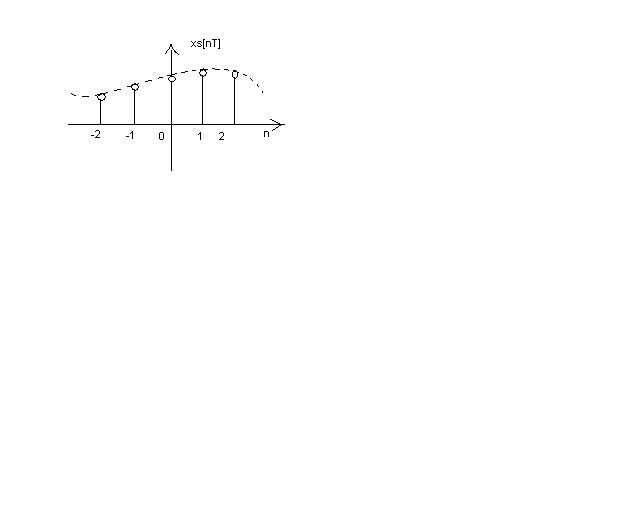
x[n]=discrete time signal
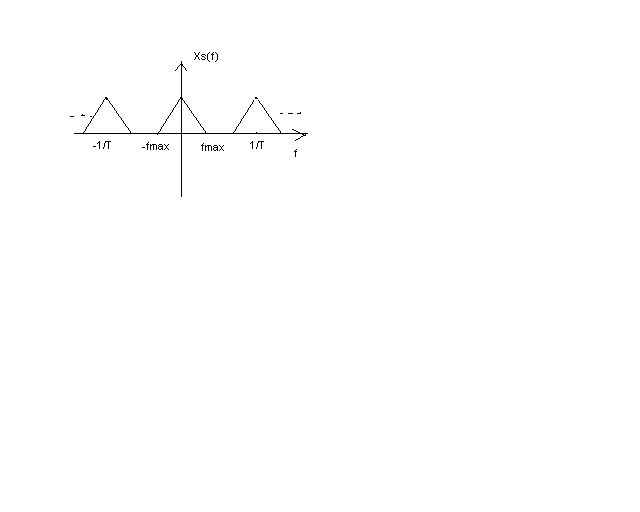
Background: DTFT Xd(ejw)= ∑n=-∞∞ xd[n]e-jwn; -----(1) Sampling, xs(t)=xc(t)pT(t)= ∑n=-∞∞ xc[nTs] δ(t-nTs), where pT(t)= ∑n=-∞∞ δ(t-nTs)
Xs(f)= CTFT{ ∑n=-∞∞ xc[nTs] δ(t-nTs)}
where 1. CTFT{δ(t-nTs)}=∫- ∞∞ δ(t-nTs)e-j2πftdt=e-j2πfnTs
2. xc[nTs] is a function of a variable n, and can be rewritten as x[n]
Therefore, Xs(f)= ∑n=-∞∞ x[n]e-j2πfnTs OR X(w)= ∑n=-∞∞ x[n]e-j2πwnTs -------(2)
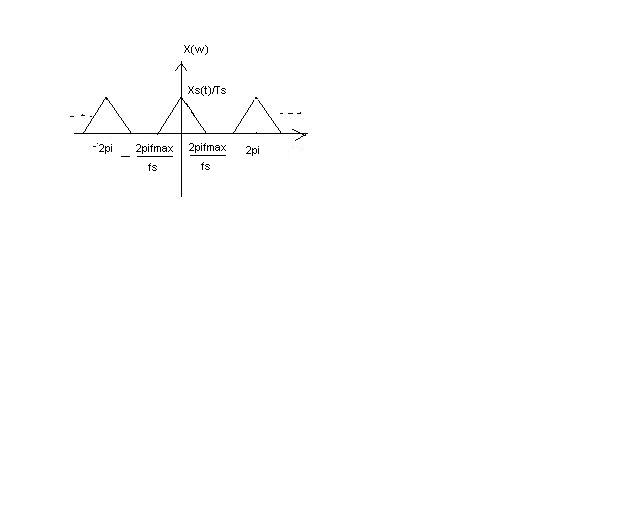
If 2πTs=1, fs=2π, equation (2) can be rewritten as ∑n=-∞∞ x[n]e-jwn,(3)
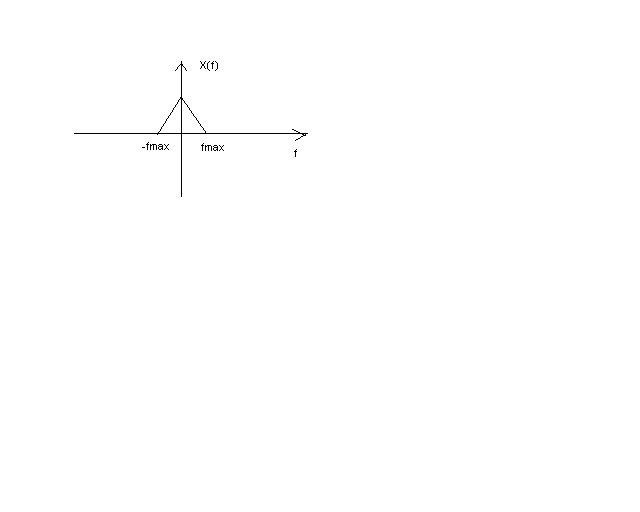
What we can conclude from here is that: if we rescale sampling rate fs as 2π, the sampling signals- a train of impulses can be redrawn to DT signals. The complete expression is X(ejw)=Xs(w/(2πTs))=1/Ts∑n=-∞∞ Xc(w/(2πTs)-n/Ts) We rescaled the original fmax as 2πfmax/fs; also, the amplitude was fs times the initial amplitude from xs(t).
