| Line 30: | Line 30: | ||
<math>x[n]=1 + (\sqrt{2}e^{5} - j\sqrt{2}e^5)e^{j(3\pi/2*n)}</math> | <math>x[n]=1 + (\sqrt{2}e^{5} - j\sqrt{2}e^5)e^{j(3\pi/2*n)}</math> | ||
| − | find the period N. <math>\omega_0=3\pi/2</math>. <math>P=2\pi/\omega_0=4/3</math>. The LCM of 1 and 4/3 is | + | find the period N. <math>\omega_0=3\pi/2</math>. <math>P=2\pi/\omega_0=4/3</math>. The LCM of 1 and 4/3 is 4. Therefore N=4 |
Choose values of <math>a_k</math> that match the forier series repersentation of x[n] | Choose values of <math>a_k</math> that match the forier series repersentation of x[n] | ||
| − | <math>x[n]=\sum_{k=<n>}^{}a_ke^{jk(2\pi/ | + | <math>x[n]=\sum_{k=<n>}^{}a_ke^{jk(2\pi/4)n}</math> |
<math>a_0=1</math> | <math>a_0=1</math> | ||
| − | <math> | + | <math>a_3=\sqrt{2}e^{5} - j\sqrt{2}e^5</math> |
1)b) | 1)b) | ||
| Line 48: | Line 48: | ||
<math>(1/N)*\sum_{n=<N>}|x[n]|^2=\sum_{k=<N>}|a_k|^2</math> | <math>(1/N)*\sum_{n=<N>}|x[n]|^2=\sum_{k=<N>}|a_k|^2</math> | ||
| − | <math>(1/N)*\sum_{n=<N>}|x[n]|^2=1^2+|(-2je^{\pi/4}e^{5})|^2=1 + | + | <math>(1/N)*\sum_{n=<N>}|x[n]|^2=1^2+|(-2je^{\pi/4}e^{5})|^2=1 + 4e^{10}</math> |
| − | <math>(1/N)*\sum_{n=<N>}|x[n]|^2=1 + | + | <math>(1/N)*\sum_{n=<N>}|x[n]|^2=1 + 4e^{10}</math> |
| Line 68: | Line 68: | ||
| − | Periodic signals have the fourier transform of <math>X(e^{jw})=\sum_{k=-\infty}^{infty}2\pi a_k\delta(\omega-k\omega_0)</math> | + | Periodic signals have the fourier transform of <math>X(e^{jw})=\sum_{k=-\infty}^{\infty}2\pi a_k\delta(\omega-k\omega_0)</math> |
T=5 | T=5 | ||
| Line 78: | Line 78: | ||
<math>Y(e^{j\omega})=X(e^{j\omega})H(e^{j\omega})</math> | <math>Y(e^{j\omega})=X(e^{j\omega})H(e^{j\omega})</math> | ||
| − | <math>Y(e^{j\omega})=\sum_{k=-\infty}^{infty}2\pi a_k\delta(\omega-k\omega_0)(1/(3+j | + | <math>Y(e^{j\omega})=\sum_{k=-\infty}^{\infty}2\pi a_k\delta(\omega-k\omega_0)(1/(3+j\omega))</math> |
| − | <math>Y(e^{j\omega})=\sum_{k=-\infty}^{infty}2\pi a_k(1/(3+jk | + | <math>Y(e^{j\omega})=\sum_{k=-\infty}^{\infty}2\pi a_k(1/(3+jk\omega_0)\delta(\omega-k\omega_0))</math> |
| − | <math>Y(e^{j\omega})=\sum_{k=-\infty}^{infty}2\pi(a_k/(3+jk2 | + | <math>Y(e^{j\omega})=\sum_{k=-\infty}^{\infty}2\pi(a_k/(3+jk2\pi/5))\delta(\omega-k\omega_0))</math> |
| − | notice <math>b_k=a_k/(3+jk2 | + | notice <math>b_k=a_k/(3+jk2\pi/5)</math> |
| − | <math>b_{-3}=-4j/(3-j6 | + | <math>b_{-3}=-4j/(3-j6\pi/5)</math> |
| − | <math>b_{-1}=2/(3-j2 | + | <math>b_{-1}=2/(3-j2\pi/5)</math> |
| − | <math>b_{1}=2/(3+j2 | + | <math>b_{1}=2/(3+j2\pi/5)</math> |
| − | <math>b_{3}=4j/(3+j6 | + | <math>b_{3}=4j/(3+j6\pi/5</math> |
<math>b_k=0</math> for all other k | <math>b_k=0</math> for all other k | ||
Latest revision as of 10:10, 22 July 2008
Read the discussion page using the discussion tab above. (Aung - 11:09 pm 07/18/08)
Contents
Problems
1)a)If a discrete time singal x[n] is periodic with period N, then the Fourier series coefficients $ a_k $ of the signal x[n] is also periodic with period N. For the periodic signal x[n], find the values of $ a_0,a_1,...,a_{N-1}. $ Express your answer in a + jb form.
$ x[n]=1 - 2je^{5+j(3\pi/2*n+\pi/4)} $
1)b)Evaluate the value of $ (1/N)*\sum_{n=<N>}|x[n]|^2 $ for the signal x[n] given in part (a).
2)a)Let's consider a continuous-time periodic signal x(t) with period T = 5 whose non-zero Fourier series coefficients $ a_k $ are given by
$ a_1=a_{-1}=2,a_3=a*_{-3}=4j $
If x(t) is the input to a particular LTI system characterized by the frequency response
$ H(j\omega)=1/(3+j\omega) $
then the output is y(t).
Is the output signal y(t) periodic? Answer YES or NO only.
2)b)If your answer to part (a) is YES, then let $ b_k $ be the fourier series coefficients of y(t) and find the values of $ b_k $. You need not simplify the complex numbers. If your answer to part (a) is NO, then explain why y(t) is not periodic.
Solutions
1)a) Change the equation to look like a forier series. $ x[n]=1-2je^{5+j(3\pi/2*n+\pi/4)}= $ $ x[n]=1 - 2je^{\pi/4}e^{5}e^{j(3\pi/2)*n}= $ $ x[n]=1 + (\sqrt{2}e^{5} - j\sqrt{2}e^5)e^{j(3\pi/2*n)} $
find the period N. $ \omega_0=3\pi/2 $. $ P=2\pi/\omega_0=4/3 $. The LCM of 1 and 4/3 is 4. Therefore N=4
Choose values of $ a_k $ that match the forier series repersentation of x[n]
$ x[n]=\sum_{k=<n>}^{}a_ke^{jk(2\pi/4)n} $
$ a_0=1 $
$ a_3=\sqrt{2}e^{5} - j\sqrt{2}e^5 $
1)b) Some energy therom states that: $ \sum_{n=<N>}|x[n]|^2=N*sum_{k=<N>}|a_k|^2 $
Therefore:
$ (1/N)*\sum_{n=<N>}|x[n]|^2=\sum_{k=<N>}|a_k|^2 $
$ (1/N)*\sum_{n=<N>}|x[n]|^2=1^2+|(-2je^{\pi/4}e^{5})|^2=1 + 4e^{10} $
$ (1/N)*\sum_{n=<N>}|x[n]|^2=1 + 4e^{10} $
--Krtownse 15:53, 18 July 2008 (EDT)
2)a) YES
2)b)First thing: state $ a_k $ clearly:
$ a_{-3}=-4j $
$ a_{-1}=2 $
$ a_{1}=2 $
$ a_{3}=4j $
Periodic signals have the fourier transform of $ X(e^{jw})=\sum_{k=-\infty}^{\infty}2\pi a_k\delta(\omega-k\omega_0) $
T=5
$ w_0=2\pi/T=2\pi/5 $
y(t)=x(t)*h(t) (convulution)
$ Y(e^{j\omega})=X(e^{j\omega})H(e^{j\omega}) $
$ Y(e^{j\omega})=\sum_{k=-\infty}^{\infty}2\pi a_k\delta(\omega-k\omega_0)(1/(3+j\omega)) $
$ Y(e^{j\omega})=\sum_{k=-\infty}^{\infty}2\pi a_k(1/(3+jk\omega_0)\delta(\omega-k\omega_0)) $
$ Y(e^{j\omega})=\sum_{k=-\infty}^{\infty}2\pi(a_k/(3+jk2\pi/5))\delta(\omega-k\omega_0)) $
notice $ b_k=a_k/(3+jk2\pi/5) $
$ b_{-3}=-4j/(3-j6\pi/5) $
$ b_{-1}=2/(3-j2\pi/5) $
$ b_{1}=2/(3+j2\pi/5) $
$ b_{3}=4j/(3+j6\pi/5 $
$ b_k=0 $ for all other k
--Krtownse 19:55, 18 July 2008 (EDT)

Problems
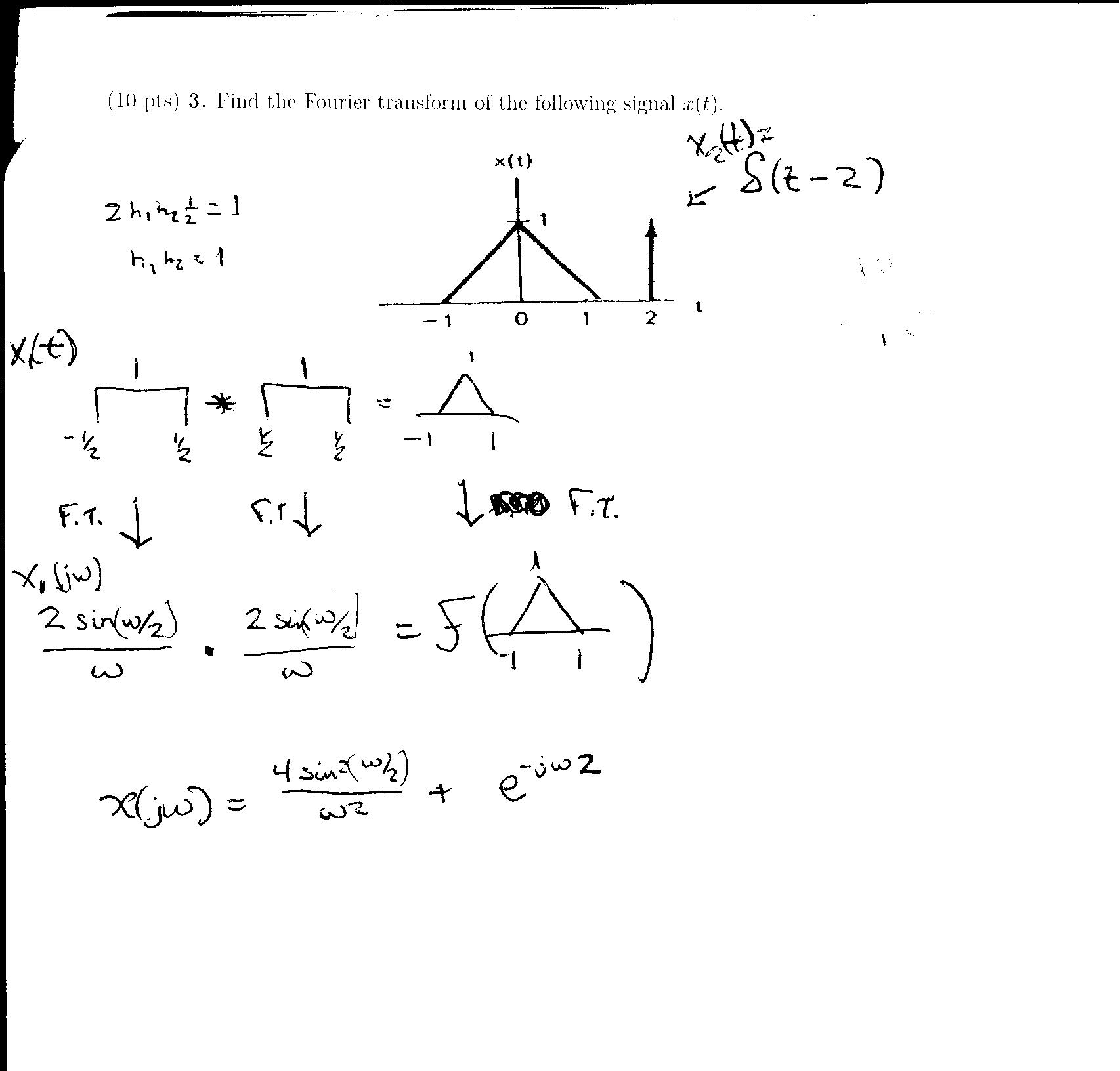
3. Find the Fourier Transform of the following signal x(t)
We were given that x(t) was a triangle with height 1 and a base from -1 to 1, plus a delta function shifted by 2.
For the sake of this problem we'll say: $ x(t) = x_1(t) + x_2(t) similarly; x(j\omega) = x_1(j\omega) + x_2(j\omega) $
The delta part of the function is farely simple, so we'll say
$ x_2(t) = \delta(t-2) $
therefore
$ x_2(j\omega) = e^{-2j\omega} $
The tricky part is the triangle, which we'll say is:
$ x_1(t) $ = square wave from -.5 to .5 w/height of 1 convulved with a square wave from -.5 to .5 w/height of 1.
Lecture 15 pg. 18 gives details of the properties for these types of functions.
Take a look at the image below for a visual representation of $ x_1(t) $
The solution to this problem is the answer given below $ x_1(t) $
--Pmavery_OldKiwi 17:34 p.m. 21, July 2008
Problems
4.
Solutions
Part A
Parts B & C
--Pmavery_OldKiwi 17:45 p.m. 21, July 2008