| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | In the K Nearest Neighbor (K-NN)technique, we need to store n samples of the training set. If n is very large, this storage will require a big memory. Moreover, the computation for the distances from a new sample to n training samples will be very huge. Editting technique is a way to reduce this memory and computation expenses. | + | In the K Nearest Neighbor (K-NN) technique, we need to store n samples of the training set. If n is very large, this storage will require a big memory. Moreover, the computation for the distances from a new sample to n training samples will be very huge. Editting technique is a way to reduce this memory and computation expenses. |
The basic idea of this technique is to remove away from the training set any samples which contribute to the misclassification. | The basic idea of this technique is to remove away from the training set any samples which contribute to the misclassification. | ||
| Line 6: | Line 6: | ||
[[Image:Fig1_OldKiwi.jpg]] | [[Image:Fig1_OldKiwi.jpg]] | ||
| + | |||
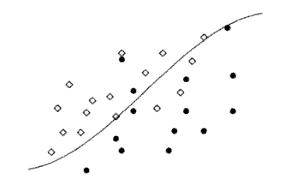
'''Figure 1:''' Two overlapping distributions along with the Bayes decision boundary | '''Figure 1:''' Two overlapping distributions along with the Bayes decision boundary | ||
[[Image:Fig2_OldKiwi.jpg]] | [[Image:Fig2_OldKiwi.jpg]] | ||
| + | |||
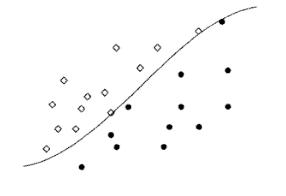
'''Figure 2:''' The distributions in Fig. 1 after removing misclassified samples | '''Figure 2:''' The distributions in Fig. 1 after removing misclassified samples | ||
The followings are the algorithm of the editing technique for the K-NN rule: | The followings are the algorithm of the editing technique for the K-NN rule: | ||
| − | 1. Divide the training set to N partitions: <math>R_1,R_2,...,R_N</math>. | + | '''1.''' Divide the training set <math>R</math> to <math> N</math> partitions: <math>R_1,R_2,...,R_N</math>. |
| − | 2. Classify the samples in the set <math>R_i</math> using K-NN with the union of the "next" <math>M</math> sets <math>R_{\left( {i + 1} \right)\bmod N} \cup ... \cup R_{\left( {i + M - 1} \right)\bmod N}</math> as the design set, for <math>i=1,...,N</math> where <math> | + | |
| + | '''2.''' Classify the samples in the set <math>R_i</math> using K-NN with the union of the "next" <math>M</math> sets <math>R_{\left( {i + 1} \right)\bmod N} \cup ... \cup R_{\left( {i + M - 1} \right)\bmod N}</math> as the design set, for <math>i=1,...,N</math> where <math>1 \le M \le N - 1</math>. Let <math>S </math> be the set of misclassified samples. | ||
| + | |||
| + | '''3.''' <math>R=R-S</math> | ||
| + | |||
| + | '''4.''' Repeat to 1 until <math>S</math> is empty. | ||
| + | |||
| + | |||
| + | Reference: Andrew Webb, "Statistical Pattern Recognition" , 2nd, Wiley, 2001. | ||
Latest revision as of 10:48, 7 April 2008
In the K Nearest Neighbor (K-NN) technique, we need to store n samples of the training set. If n is very large, this storage will require a big memory. Moreover, the computation for the distances from a new sample to n training samples will be very huge. Editting technique is a way to reduce this memory and computation expenses.
The basic idea of this technique is to remove away from the training set any samples which contribute to the misclassification.
Figure 1 below shows the overlapping distributions of the training set of two classes along with their Bayes boundary. In the figure, in each region, we can observe some samples which are misclassified by Bayes rule. Removing these misclassfied sample will generate two homogeneous sets of samples with the a nearest neighbor decision boundary approximate the Bayes decision boundary (Fig. 2).
Figure 1: Two overlapping distributions along with the Bayes decision boundary
Figure 2: The distributions in Fig. 1 after removing misclassified samples
The followings are the algorithm of the editing technique for the K-NN rule:
1. Divide the training set $ R $ to $ N $ partitions: $ R_1,R_2,...,R_N $.
2. Classify the samples in the set $ R_i $ using K-NN with the union of the "next" $ M $ sets $ R_{\left( {i + 1} \right)\bmod N} \cup ... \cup R_{\left( {i + M - 1} \right)\bmod N} $ as the design set, for $ i=1,...,N $ where $ 1 \le M \le N - 1 $. Let $ S $ be the set of misclassified samples.
3. $ R=R-S $
4. Repeat to 1 until $ S $ is empty.
Reference: Andrew Webb, "Statistical Pattern Recognition" , 2nd, Wiley, 2001.