m (→Observation 2) |
(Removed broken (accidentaly replaced) animation which was not relavant to the discussion any more.) |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
In this derivation, we assume the dimension of the space being projected to, k, is k=1. | In this derivation, we assume the dimension of the space being projected to, k, is k=1. | ||
| − | We attempt to find a linear projection (line that passes through the origin) s.t. the projected data can be "best" separated. | + | We attempt to find a linear projection (line that passes through the origin) s.t. the projected data can be "best" separated. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Assume <math>y_1,..., y_{d_1}</math> belongs to Class 1 and <math>y_{d_1+1}</math>,..., <math>y_d</math> belongs to Class 2. | Assume <math>y_1,..., y_{d_1}</math> belongs to Class 1 and <math>y_{d_1+1}</math>,..., <math>y_d</math> belongs to Class 2. | ||
| Line 16: | Line 12: | ||
=== Observation 1 === | === Observation 1 === | ||
| − | <math>m1 = \vec{w} \frac{1}{d_1} \sum_{i=1}^{d_1} y_i</math>, which is the projection of the sample mean for Class 1. | + | <math>\tilde{m1} = \vec{w} \frac{1}{d_1} \sum_{i=1}^{d_1} y_i</math>, which is the projection of the sample mean for Class 1. |
Also, <math>\tilde{m_2} = \frac{1}{d-d_1}\sum_{i=d_1+1}^{d} \vec{w} \cdot y_i = \vec{w} \cdot m_2</math> . | Also, <math>\tilde{m_2} = \frac{1}{d-d_1}\sum_{i=d_1+1}^{d} \vec{w} \cdot y_i = \vec{w} \cdot m_2</math> . | ||
Latest revision as of 10:50, 22 April 2008
See also: Fisher Linear Discriminant_OldKiwi
In this derivation, we assume the dimension of the space being projected to, k, is k=1.
We attempt to find a linear projection (line that passes through the origin) s.t. the projected data can be "best" separated.
Assume $ y_1,..., y_{d_1} $ belongs to Class 1 and $ y_{d_1+1} $,..., $ y_d $ belongs to Class 2.
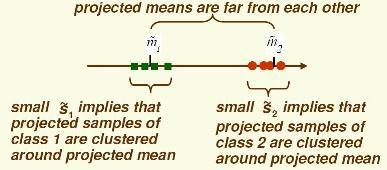
Consider the sample mean of the projected data for each class
$ \tilde{m_1} = \frac{1}{d_1} \sum_{i=1}^{d_1} \pi(y_i) = \frac{1}{d_1}\sum_{i=1}^{d_1} \vec{w} \cdot y_i $, if $ ||\omega || =1 $
Observation 1
$ \tilde{m1} = \vec{w} \frac{1}{d_1} \sum_{i=1}^{d_1} y_i $, which is the projection of the sample mean for Class 1.
Also, $ \tilde{m_2} = \frac{1}{d-d_1}\sum_{i=d_1+1}^{d} \vec{w} \cdot y_i = \vec{w} \cdot m_2 $ .
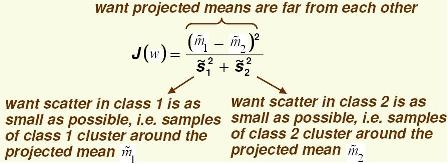
Consider the scatter projections:
$ \tilde{S_1}^2 = \sum_{i=1}^{d_1} (\vec{w} \cdot y_i - \tilde{m_1})^2 $
$ \tilde{S_2}^2 = \sum_{i=d_1+1}^{d} (\vec{w} \cdot y_i - \tilde{m_2})^2 $
Define the following cost function, $ J(\vec{w}) = \frac{|\tilde{m1} - \tilde{m2}|^2}{\tilde{S_1}^2+ \tilde{S_2}^2} $ .
The above equation is the "Fisher linear discriminant_OldKiwi".
Observation 2
Demanding $ ||\tilde{m_1} - \tilde{m_2}|| $ to be maximized would not do, since $ ||\tilde{m_1} - \tilde{m_2}|| = |\vec{w} \cdot m_1 - \vec{w} \cdot m_2 | = | \vec{w} \cdot (m_1 - m_2)| \rightarrow \infty $
Need to fix $ || \omega || = 1 $ , resulting in a Constrained Optimization Problem.
By dividing by $ \tilde{S_1}^2 + \tilde{S_2}^2 $ we demand that $ \vec{w} \cdot (m_1 - m_2) $ be large in comparison with the scatter. This allows you to bypass the coordinate scale problem because $ J(\vec{w}) $ is independent of $ \omega $.
$ |\tilde{m_1} - \tilde{m_2}|^2 = | w(m_1 - m_2)|^2 = |w|^2 | \frac{w}{|w|}(m_1-m_2)|^2 $
Similarly,
$ \tilde{S_1}^2 = \sum (\vec{w}(y_i - m_1))^2 = |w|^2 \sum (\frac{w}{|W|} (y_i - m_1))^2 $
and,
$ \tilde{S_2}^2 = \sum (\vec{w}(y_i - m_1))^2 = |w|^2 \sum (\frac{w}{|W|} (y_i - m_2))^2 $
and,
$ J(\vec{w}) = \frac{|m_1-m_2|^2}{S_1^2+S_2^2} =\frac{|w|^2 | \frac{w}{|w|}(m_1-m_2)|^2}{|w|^2(\sum (\frac{w}{|W|} (y_i - m_1))^2 + \sum (\frac{w}{|W|} (y_i - m_2))^2 )} $ is independent of $ ||\omega|| $.
Importance of scatter:
If we find $ \omega $ which makes $ Jw $ large, we are guaranteed that the classes are well-separated.
We can write $ Jw $ using matrices:
$ J(\vec{w}) = \frac{\vec{w}^{\top}S_B \vec{w}}{\vec{w}^{\top}S_w \vec{w}} $, which is called the "[Generalized Rayleigh Quotient]".
(Lecture 11_OldKiwi begins here)
Last time we considered $ J(\vec{w})=\frac {{\vec{w}}^{T}{S}_{B}\vec{w}} {{\vec{w}}^{T}{S}_{W}\vec{w}} $, explicit function of $ \vec{w} $
one can do this because
(numerator of J) = $ \| \tilde{m_1}-\tilde{m_2} \|^2 = \| w(m_1-m_2) \|^2 = \| (m_1-m_2)^T w \|^2 $
$ =w^T (m_1-m_2)(m_1^T-m_2^T)w $
where, $ (m_1-m_2)(m_1^T-m_2^T) =S_B $ is 'between class scatter matrix'.
(denominator of J) = $ \tilde{s_1}^2 + \tilde{s_2}^2 $
$ \tilde{s_1}^2 =\displaystyle \sum_{\vec y \; in \; class} (w y_i- \tilde{m_i} )^2 $
$ = \displaystyle \sum_{\vec{y} \; in \; class} w^T (y_i-m_i)(y_i^T-m_i^T)w $
$ w^T \displaystyle \sum_{\vec{y} \; in \; class} (y_i-m_i)(y_i^T-m_i^T)w $
where, $ \displaystyle \sum_{\vec y \; in \; class} (y_i-m_i)(y_i^T-m_i^T) =S_w $ is 'within class scattter matrix'.