| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:MA453Spring2009Walther]] | [[Category:MA453Spring2009Walther]] | ||
| − | If we draw a 'non-square rectangle' as shown: [[Image: | + | ---- |
| + | |||
| + | Edition 6: # 13: | ||
| + | Q: Describe the symmetries of a nonsquare rectangle. Construct the corresponding Cayley table for it. | ||
| + | |||
| + | A: The symmetries are relatively easy. See Ed. 6 page 32 for the symmetries of a square. The only symmetries that apply to our particular rectangle are: a flip about the vertical axis (V); a flip about the horizontal axis (H); rotation of 0 degrees (R0) and a rotation of 180 degrees (R180). | ||
| + | |||
| + | The Cayley table is relatively straight forward. The trickiest part was identifying the rotations followed by flips, or vice versa. The best tip is to draw it out for yourself, and remember that each element shows once in each column and row. | ||
| + | |||
| + | Hint: Vertical flip * R180 (rotation first, flip second) => Horizontal flip | ||
| + | Vertical flip * Horizontal flip (H first, V second) => Rotation of 180 degrees | ||
| + | ---- | ||
| + | |||
| + | If we draw a 'non-square rectangle' as shown: [[Image:Rect.jpg]] | ||
| + | |||
| + | The ''Caylay Table'' I found was: [[Image:Rect-caylay.jpg]] | ||
| + | where 1 is do nothing, and R is a 180 deg rotation in either direction | ||
| + | |||
| + | I got the same thing. --[[User:Aifrank|Aifrank]] 13:16, 28 January 2009 (UTC) | ||
| + | |||
Ignore everything below, wrong chapter!!--[[User:Bcaulkin|Bcaulkin]] 22:58, 27 January 2009 (UTC) | Ignore everything below, wrong chapter!!--[[User:Bcaulkin|Bcaulkin]] 22:58, 27 January 2009 (UTC) | ||
Latest revision as of 08:16, 28 January 2009
Edition 6: # 13: Q: Describe the symmetries of a nonsquare rectangle. Construct the corresponding Cayley table for it.
A: The symmetries are relatively easy. See Ed. 6 page 32 for the symmetries of a square. The only symmetries that apply to our particular rectangle are: a flip about the vertical axis (V); a flip about the horizontal axis (H); rotation of 0 degrees (R0) and a rotation of 180 degrees (R180).
The Cayley table is relatively straight forward. The trickiest part was identifying the rotations followed by flips, or vice versa. The best tip is to draw it out for yourself, and remember that each element shows once in each column and row.
Hint: Vertical flip * R180 (rotation first, flip second) => Horizontal flip Vertical flip * Horizontal flip (H first, V second) => Rotation of 180 degrees
If we draw a 'non-square rectangle' as shown: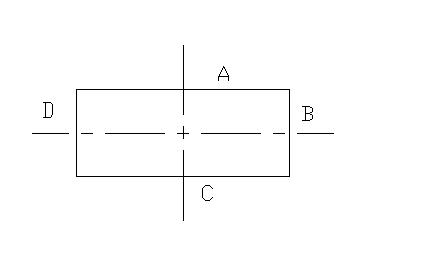 
The Caylay Table I found was: 
where 1 is do nothing, and R is a 180 deg rotation in either direction
I got the same thing. --Aifrank 13:16, 28 January 2009 (UTC)
Ignore everything below, wrong chapter!!--Bcaulkin 22:58, 27 January 2009 (UTC)
"An abstract algebra teacher intended to give a typist a list of nine integers that form a group under multiplication modulo 91. Instead, one of the nine integers was left out, so that the list appeared as 1, 9, 16, 22, 53, 74, 79, 81. Which integer was left out?"
It's easy to list all the cosets of (Z mod 91, *), so that cannot possibly what this question is asking about.
- 1=1*1, 9=3*3, 22=2*11, 53=53*1, 74=2*37, 79=79*1, 81=9*9=3*3*3*3
All but one has only two prime factors. Prime Factorization Table was helpful for this...
The differences between each integer is 8, 13, 31, 21, 5, 2
- Nothing special there...
Either there's a trick, or this is insanely easy... (perhaps I'm slow...)
