| (One intermediate revision by one other user not shown) | |||
| Line 22: | Line 22: | ||
[[Image:q2_MA453Fall2008walther.jpg]] | [[Image:q2_MA453Fall2008walther.jpg]] | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | [[Image:453math_hw0001_MA453Fall2008walther.jpg]] | ||
| + | --[[User:Akcooper|Akcooper]] 16:09, 3 October 2008 (UTC) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | If A_3 is normal in S_3, then for every element of S_3, the left and right cosets of A_3 are equal. | ||
| + | A_3 = {1,l,r} and S_3 = {1,l,r,a,b,c} | ||
| + | |||
| + | 1*{1,l,r} = {1,l,r} = {1,l,r}*1 | ||
| + | |||
| + | l*{1,l,r} = {1,l,r} = {1,l,r}*l | ||
| + | |||
| + | r*{1,l,r} = {1,l,r} = {1,l,r}*r | ||
| + | |||
| + | a*{1,l,r} = {a,b,c} = {1,l,r}*a | ||
| + | |||
| + | b*{1,l,r} = {a,b,c} = {1,l,r}*b | ||
| + | |||
| + | c*{1,l,r} = {a,b,c} = {1,l,r}*c | ||
| + | |||
| + | Left and right cosets of A_3 for every element in S_3 match. This proves A_3 is normal in S_3. | ||
| + | |||
| + | -Ozgur | ||
Latest revision as of 14:12, 4 October 2008
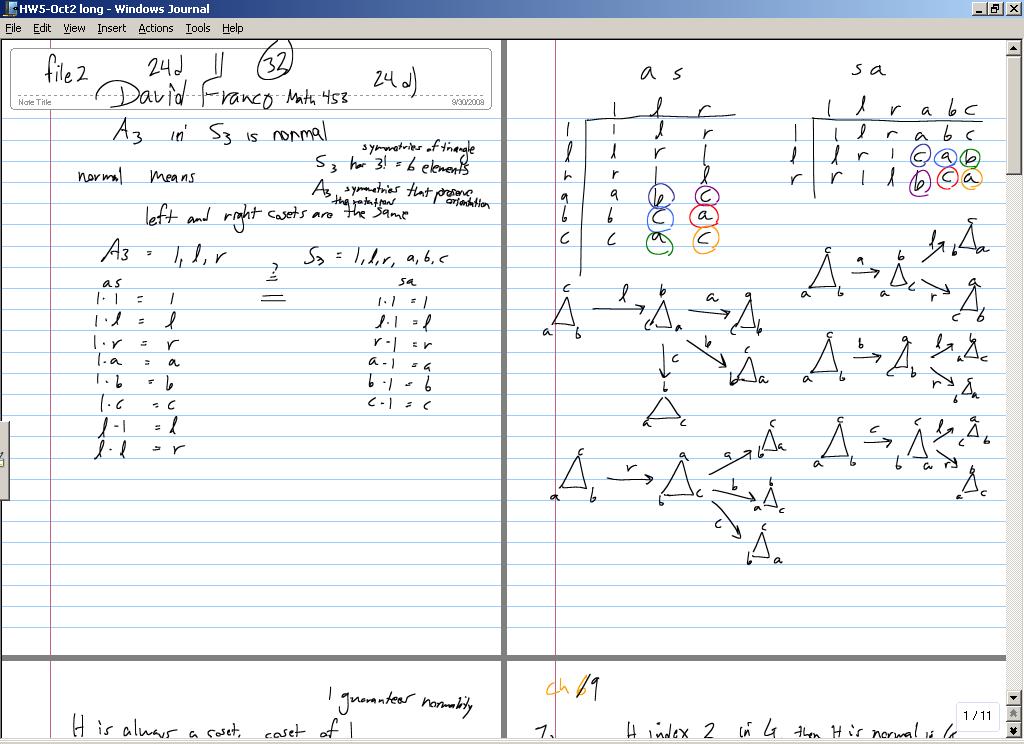
Prove that A_3 inside S_3 is normal.
To prove this use the definition that if a group is normal then as a collection left cosets equal right cosets.
I used S_3 to equal a symmetric triangle with {1,l,r,a,b,c} A_3 the group of even permutations in S_3 which are {1,l,r}
Right Cosets Left Cosets
A_3 * 1 1 * A_3
--Robertsr 19:58, 1 October 2008 (UTC)
I used what we proved in Ch 9 problem 7 to prove this. In that problem, we proved that if H has index 2 in G, then H is normal in G. A_3 has index 2 in S_3 because by Corollary 1 of Lagrange's Theorem, the index of H in G = |G|/|H|. In this case, G = S_3 and H = A_3. We know that |S_3| = 3!, and by Theorem 5.7 we know that |A_3| = 3!/2. Therefore, the index of A_3 in S_3 = 3!/(3!/2) = 2, and A_3 is normal in S_3.
I used a similar method found above. I knew that |S_3| = 3! and |A_3| = 3!/2 and the index of these two was |A_3|/|S_3| which gives you an index of 2. Then I remembered a previous problem I did on this hw and remembered that if a subgroup has order 2 then the group is normal. In this case the subgroup was S_3 and A_3 was the group. Therefore A_3 and S_3 are normal
 --Akcooper 16:09, 3 October 2008 (UTC)
--Akcooper 16:09, 3 October 2008 (UTC)
If A_3 is normal in S_3, then for every element of S_3, the left and right cosets of A_3 are equal.
A_3 = {1,l,r} and S_3 = {1,l,r,a,b,c}
1*{1,l,r} = {1,l,r} = {1,l,r}*1
l*{1,l,r} = {1,l,r} = {1,l,r}*l
r*{1,l,r} = {1,l,r} = {1,l,r}*r
a*{1,l,r} = {a,b,c} = {1,l,r}*a
b*{1,l,r} = {a,b,c} = {1,l,r}*b
c*{1,l,r} = {a,b,c} = {1,l,r}*c
Left and right cosets of A_3 for every element in S_3 match. This proves A_3 is normal in S_3.
-Ozgur