| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | If you name the | + | =[[HW2_MA453Fall2008walther|HW2]], Chapter 1 problem 13, Discussion, [[MA453]], [[user:walther|Prof. Walther]]= |
| + | |||
| + | Problem Statement: | ||
| + | |||
| + | '''Can somebody please write the problem statement?''' | ||
| + | |||
| + | ------- | ||
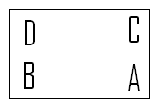
| + | If you name the vertices of the four rectangles A, B, C, and D. | ||
The rectangle would appear thus: | The rectangle would appear thus: | ||
| Line 6: | Line 13: | ||
The rectangle would have four transformations: | The rectangle would have four transformations: | ||
| − | Rotation of 0º (or 360º) : <math>R_{ | + | Rotation of 0º (or 360º) : <math>R_{0}</math> |
[[Image:R0_MA453Fall2008walther.png]] | [[Image:R0_MA453Fall2008walther.png]] | ||
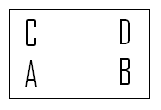
| − | Rotation of 180º: <math>R_{ | + | Rotation of 180º: <math>R_{180}</math> |
[[Image:R180_MA453Fall2008walther.png]] | [[Image:R180_MA453Fall2008walther.png]] | ||
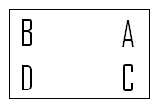
| − | Flip About a Horizontal Axis: H | + | Flip About a Horizontal Axis: <math>H</math> |
[[Image:H_MA453Fall2008walther.png]] | [[Image:H_MA453Fall2008walther.png]] | ||
| − | Flip About a Vertical Axis: V | + | Flip About a Vertical Axis: <math>V</math> |
[[Image:V_MA453Fall2008walther.png]] | [[Image:V_MA453Fall2008walther.png]] | ||
From this, the Cayley table can easily be constructed. | From this, the Cayley table can easily be constructed. | ||
| + | ---- | ||
| + | [[HW2_MA453Fall2008walther|Back to HW2]] | ||
| + | |||
| + | [[Main_Page_MA453Fall2008walther|Back to MA453 Fall 2008 Prof. Walther]] | ||
Latest revision as of 15:31, 22 October 2010
HW2, Chapter 1 problem 13, Discussion, MA453, Prof. Walther
Problem Statement:
Can somebody please write the problem statement?
If you name the vertices of the four rectangles A, B, C, and D.
The rectangle would appear thus:
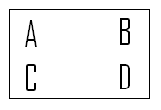
The rectangle would have four transformations:
Rotation of 0º (or 360º) : $ R_{0} $
Rotation of 180º: $ R_{180} $
Flip About a Horizontal Axis: $ H $
Flip About a Vertical Axis: $ V $
From this, the Cayley table can easily be constructed.