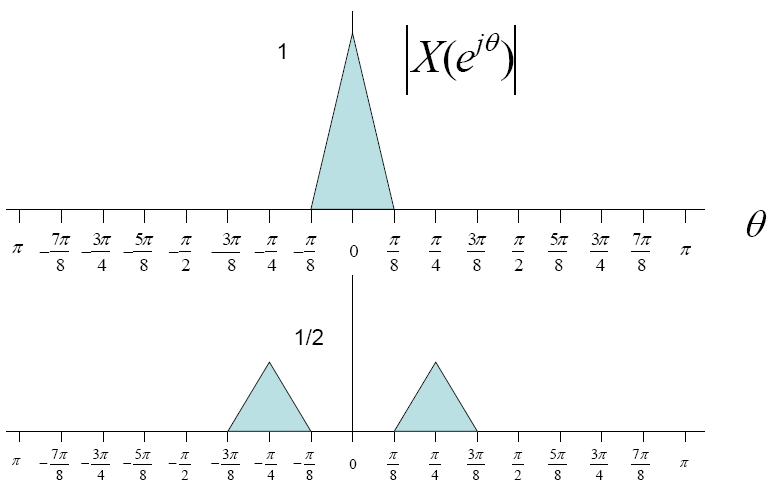| Line 4: | Line 4: | ||
Now suppose the input signal was multiplied by a cosine wave then the fourier transform of the wave would look as follows | Now suppose the input signal was multiplied by a cosine wave then the fourier transform of the wave would look as follows | ||
| − | <math>x(t)*cos(t)</math> ⇒ <math>\frac{1}{2}[X(e^{j(\theta - \pi/4)}) | + | <math>x(t)*cos(\frac{\pi t}{4})</math> ⇒ <math>\frac{1}{2}[X(e^{j(\theta - \pi/4)}) |
+ X(e^{j(\theta + \pi/4)}) ]</math>.<br> | + X(e^{j(\theta + \pi/4)}) ]</math>.<br> | ||
Latest revision as of 09:24, 24 October 2008
Now we know that
$ x(t) $ ⇒ $ X(\omega) $
Now suppose the input signal was multiplied by a cosine wave then the fourier transform of the wave would look as follows
$ x(t)*cos(\frac{\pi t}{4}) $ ⇒ $ \frac{1}{2}[X(e^{j(\theta - \pi/4)}) + X(e^{j(\theta + \pi/4)}) ] $.
In short we are getting two side bands which look something like this