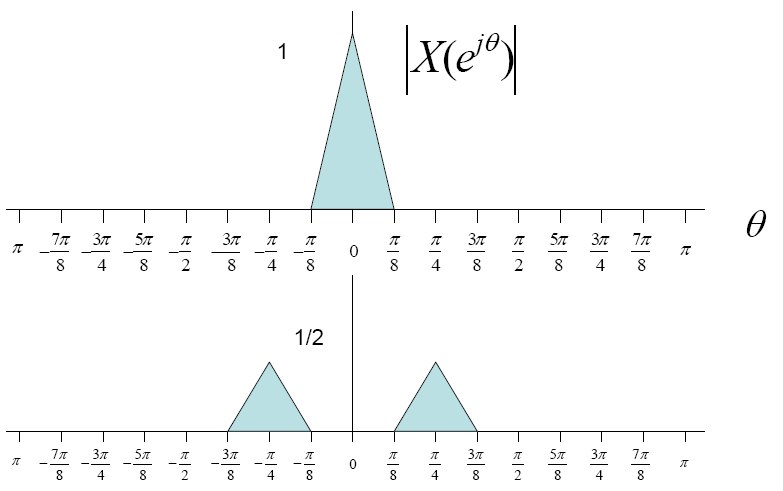(→x(t)*cos(t) ⇒ \frac{\pi}{j}[\delta(\omega - \pi) - \delta(\omega + \pi)].) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
Now suppose the input signal was multiplied by a cosine wave then the fourier transform of the wave would look as follows | Now suppose the input signal was multiplied by a cosine wave then the fourier transform of the wave would look as follows | ||
| − | + | <math>x(t)*cos(\frac{\pi t}{4})</math> ⇒ <math>\frac{1}{2}[X(e^{j(\theta - \pi/4)}) | |
| − | + X(e^{j(\theta + \pi/4)}) ]</math>. | + | + X(e^{j(\theta + \pi/4)}) ]</math>.<br> |
| + | |||
| + | In short we are getting two side bands which look something like this | ||
| + | |||
| + | [[Image:Modulation_ECE301Fall2008mboutin.gif]] | ||
Latest revision as of 09:24, 24 October 2008
Now we know that
$ x(t) $ ⇒ $ X(\omega) $
Now suppose the input signal was multiplied by a cosine wave then the fourier transform of the wave would look as follows
$ x(t)*cos(\frac{\pi t}{4}) $ ⇒ $ \frac{1}{2}[X(e^{j(\theta - \pi/4)}) + X(e^{j(\theta + \pi/4)}) ] $.
In short we are getting two side bands which look something like this