| (2 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
| − | <math> | + | <math>X=2*\sqrt{R^2-D^2}</math> if <math> 0<D<R \,\ </math> |
| − | <math> | + | <math>X=2*R \,\ </math> if <math>D=0 \,\ </math> |
| − | <math> | + | <math>X=0 \,\ </math> |
| + | else | ||
| + | |||
| + | so its PDF will be | ||
| + | <math>\int_0^{2*R} \sqrt{R^2-D^2} dD</math> | ||
Latest revision as of 09:43, 7 October 2008
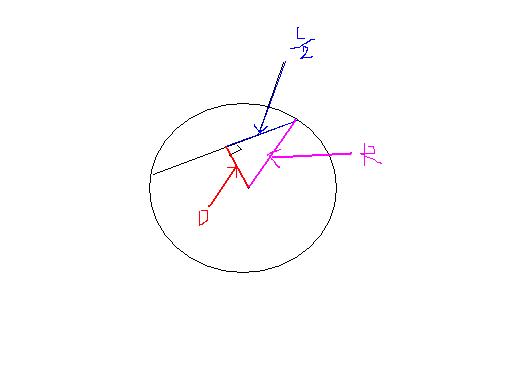
Blue line => $ L/2 = \sqrt{R^2-D^2} $
Length $ = 2*(L/2)=2*\sqrt{R^2-D^2} $
let X be the length of chord
$ X=2*\sqrt{R^2-D^2} $ if $ 0<D<R \,\ $
$ X=2*R \,\ $ if $ D=0 \,\ $
$ X=0 \,\ $ else
so its PDF will be $ \int_0^{2*R} \sqrt{R^2-D^2} dD $