(New page: == Basics of Linearity == Image:ECE301HW3.JPG We are given the following information: For input <math>x(t) = e</math> <sup>(2jt)</sup> the output <math> y(t) = te</math><sup>(-2jt)<...) |
m (→Basics of Linearity) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
We are given the following information: | We are given the following information: | ||
| − | For input <math>x(t) = e</math> <sup>(2jt)</sup> the output <math> y(t) = te</math><sup>(-2jt)</sup>. | + | * For input <math>x(t) = e</math> <sup>(2jt)</sup> the output <math> y(t) = te</math><sup>(-2jt)</sup>. |
| − | For input <math>x(t) = e</math> <sup>(-2jt)</sup> the output <math> y(t) = te</math><sup>(2jt)</sup>. | + | * For input <math>x(t) = e</math> <sup>(-2jt)</sup> the output <math> y(t) = te</math><sup>(2jt)</sup>. |
| + | |||
| + | * The system is Linear. | ||
| + | |||
| + | |||
| + | We can break down the input <math> \,\ x(t) = cos(2t) </math> into <math> \,\ x(t) = \frac{1}{2} * (e</math><sup>(j2t)</sup> <math> \,\ + e</math><sup>(-j2t)</sup><math> \,\ )</math>. | ||
| + | |||
| + | Now we can use the property of linearity to determine the output. | ||
| + | |||
| + | |||
| + | We already know the outputs of the two individual parts of <math> cos(2t) </math>. All we have to do is add them together to find the output <math> z(t) </math>. | ||
| + | |||
| + | <math> \,\ \frac{1}{2} * (e</math><sup>(j2t)</sup> <math> \,\ + e</math><sup>(-j2t)</sup><math> \,\ ) \rArr </math> SYSTEM <math> \,\ \rArr \frac{1}{2} * te</math><sup>(-2jt)</sup> + <math> \,\ \frac{1}{2} * te</math><sup>(2jt)</sup> | ||
| + | |||
| + | <math> \,\ \frac{1}{2} * te</math><sup>(-2jt)</sup> + <math> \,\ \frac{1}{2} * te</math><sup>(2jt)</sup> <math> = t * \frac{1}{2} * (e</math><sup>(j2t)</sup> <math> \,\ + e</math><sup>(-j2t)</sup><math> \,\ ) </math> | ||
| + | |||
| + | <math> t * \frac{1}{2} * (e</math><sup>(j2t)</sup> <math> \,\ + e</math><sup>(-j2t)</sup><math> \,\ ) = t*cos(2t) </math> | ||
| + | |||
| + | |||
| + | Therefore, the input signal <math> \,\ x(t) = cos(2t) </math> yields an output signal of <math> \,\ z(t) = tcos(2t) </math> | ||
Latest revision as of 12:29, 16 September 2008
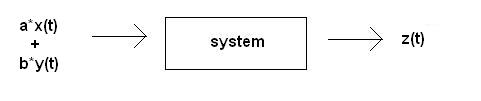
Basics of Linearity
We are given the following information:
- For input $ x(t) = e $ (2jt) the output $ y(t) = te $(-2jt).
- For input $ x(t) = e $ (-2jt) the output $ y(t) = te $(2jt).
- The system is Linear.
We can break down the input $ \,\ x(t) = cos(2t) $ into $ \,\ x(t) = \frac{1}{2} * (e $(j2t) $ \,\ + e $(-j2t)$ \,\ ) $.
Now we can use the property of linearity to determine the output.
We already know the outputs of the two individual parts of $ cos(2t) $. All we have to do is add them together to find the output $ z(t) $.
$ \,\ \frac{1}{2} * (e $(j2t) $ \,\ + e $(-j2t)$ \,\ ) \rArr $ SYSTEM $ \,\ \rArr \frac{1}{2} * te $(-2jt) + $ \,\ \frac{1}{2} * te $(2jt)
$ \,\ \frac{1}{2} * te $(-2jt) + $ \,\ \frac{1}{2} * te $(2jt) $ = t * \frac{1}{2} * (e $(j2t) $ \,\ + e $(-j2t)$ \,\ ) $
$ t * \frac{1}{2} * (e $(j2t) $ \,\ + e $(-j2t)$ \,\ ) = t*cos(2t) $
Therefore, the input signal $ \,\ x(t) = cos(2t) $ yields an output signal of $ \,\ z(t) = tcos(2t) $