(New page: The code given by the assignment was to plot 13 cycles of a 13Hz sinusoid. <pre> F0 =13; T0 =1/F0; Ts = 0.07; t = 0:Ts:13*T0; x = real(exp(j*(2*pi*F0*t-pi/2))); plot(t,x) </pre> The resu...) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
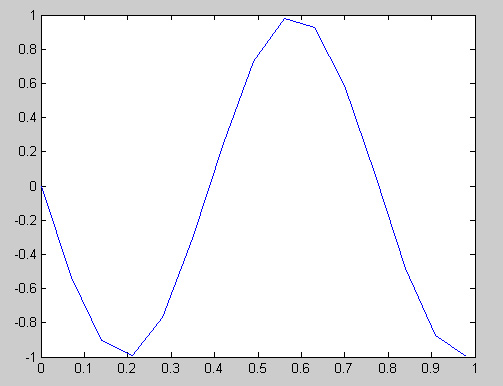
The resulting graph: | The resulting graph: | ||
| + | |||
[[Image:HW2PartBPic1_ECE301Fall2008mboutin.jpg]] | [[Image:HW2PartBPic1_ECE301Fall2008mboutin.jpg]] | ||
| − | As you can see, over | + | As you can see, over one second, the graph completes only a little bit more than one cycle. It should have thirteen cycles instead. The reason would be that the time step, Ts, was set too high and therefore was not allowing for enough values to be calculated. The remedy would be to decrease the time step by many magnitudes. Due to the fact that there needs to be 1/13 second for a cycle to complete, I decided that there should be least 1000 time steps per cycle, which gives us 13000 samples per second. |
Ts was changed to 1/13000 instead of 0.07: | Ts was changed to 1/13000 instead of 0.07: | ||
| Line 25: | Line 26: | ||
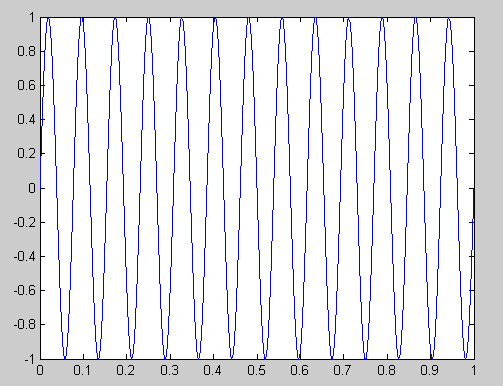
The resulting graph actually has 13 cycles over one second of time: | The resulting graph actually has 13 cycles over one second of time: | ||
| + | |||
[[Image:HW2PartBPic2_ECE301Fall2008mboutin.jpg]] | [[Image:HW2PartBPic2_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 07:34, 12 September 2008
The code given by the assignment was to plot 13 cycles of a 13Hz sinusoid.
F0 =13; T0 =1/F0; Ts = 0.07; t = 0:Ts:13*T0; x = real(exp(j*(2*pi*F0*t-pi/2))); plot(t,x)
The resulting graph:
As you can see, over one second, the graph completes only a little bit more than one cycle. It should have thirteen cycles instead. The reason would be that the time step, Ts, was set too high and therefore was not allowing for enough values to be calculated. The remedy would be to decrease the time step by many magnitudes. Due to the fact that there needs to be 1/13 second for a cycle to complete, I decided that there should be least 1000 time steps per cycle, which gives us 13000 samples per second.
Ts was changed to 1/13000 instead of 0.07:
F0 =13; T0 =1/F0; Ts = 1/13000; t = 0:Ts:13*T0; x = real(exp(j*(2*pi*F0*t-pi/2))); plot(t,x)
The resulting graph actually has 13 cycles over one second of time: