| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Definition== | ||
| + | A function is linear if there is a single unique x that corresponds to each y. | ||
| + | |||
| + | ==Linear== | ||
<math>y=e^x</math> | <math>y=e^x</math> | ||
<br> | <br> | ||
[[Image:linear_ECE301Fall2008mboutin.jpg]] | [[Image:linear_ECE301Fall2008mboutin.jpg]] | ||
<br> | <br> | ||
| − | This function is linear because for each y value has only one corresponding x | + | This function is linear because for each y value has only one corresponding x value. |
| + | ==Nonlinear== | ||
<math>y=x^4</math> | <math>y=x^4</math> | ||
<br> | <br> | ||
Latest revision as of 11:39, 12 September 2008
Definition
A function is linear if there is a single unique x that corresponds to each y.
Linear
$ y=e^x $
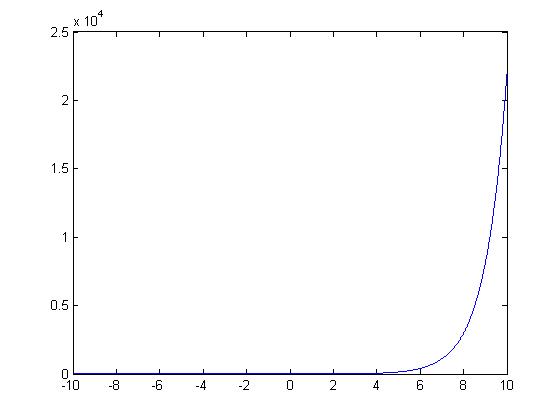
This function is linear because for each y value has only one corresponding x value.
Nonlinear
$ y=x^4 $
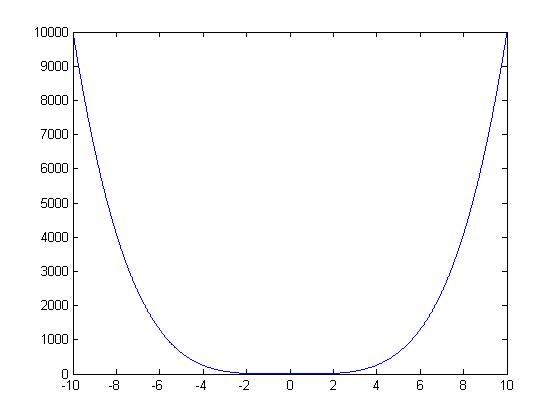
This function is not linear because for every y value there are two possible x values that could produce the same result.

