(New page: == Linearity and Time Invariance == a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class:) |
(→Linearity and Time Invariance) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Homework 2_ECE301Fall2008mboutin]] - [[HW2-A Phil Cannon_ECE301Fall2008mboutin|'''A''']] - [[HW2-B Phil Cannon_ECE301Fall2008mboutin|'''B''']] - [[HW2-C Phil Cannon_ECE301Fall2008mboutin|'''C''']] - [[HW2-D Phil Cannon_ECE301Fall2008mboutin|'''D''']] - [[HW2-E Phil Cannon_ECE301Fall2008mboutin|'''E''']] | ||
| + | |||
== Linearity and Time Invariance == | == Linearity and Time Invariance == | ||
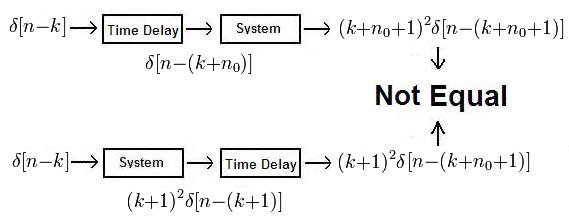
a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class: | a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class: | ||
| + | |||
| + | [[Image:Hw2E_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | b). Assuming the system were linear it would require an input <math>X[n]=u[n]\!</math> to yield <math>Y[n]=u[n-1]\!</math>. | ||
Latest revision as of 16:04, 11 September 2008
Homework 2_ECE301Fall2008mboutin - A - B - C - D - E
Linearity and Time Invariance
a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class:
b). Assuming the system were linear it would require an input $ X[n]=u[n]\! $ to yield $ Y[n]=u[n-1]\! $.