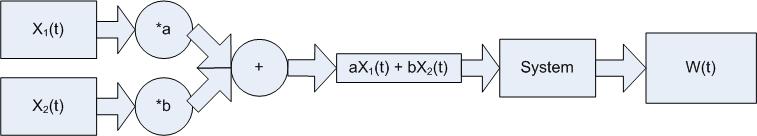(New page: == Definition == == Examples == Linear: Non-Linear:) |
(→Examples) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
| + | If Z(t) and W(t) in the following are equal the system is linear. | ||
| + | |||
| + | [[Image:Linearity Part 1_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[Image:Linearity Part 2_ECE301Fall2008mboutin.jpg]] | ||
== Examples == | == Examples == | ||
Linear: | Linear: | ||
| + | |||
| + | An example of an linear function is <math>\ y(t) = 3x(t + 8)</math> | ||
| + | |||
| + | because the result of the 1st method above yields <math>\ 3ax(t + 8) + 3bx(t + 8)</math> | ||
| + | |||
| + | and the result of the 2nd method above yields <math>\ 3[ax(t + 8) + bx(t + 8)]</math>. Because they yield the same result the system is linear. | ||
Non-Linear: | Non-Linear: | ||
| + | |||
| + | An example of a non-linear function is <math>\ y(t) = e^{x(t)} </math> | ||
| + | |||
| + | because the result of the 1st method above yields <math>\ e^{ax(t)} + e^{bx(t)}</math> | ||
| + | |||
| + | and the result of the 2nd method above yields <math>\ e^{ax(t) + bx(t)}</math>, which is not equal to the first result. | ||
Latest revision as of 10:22, 12 September 2008
Definition
If Z(t) and W(t) in the following are equal the system is linear.
Examples
Linear:
An example of an linear function is $ \ y(t) = 3x(t + 8) $
because the result of the 1st method above yields $ \ 3ax(t + 8) + 3bx(t + 8) $
and the result of the 2nd method above yields $ \ 3[ax(t + 8) + bx(t + 8)] $. Because they yield the same result the system is linear.
Non-Linear:
An example of a non-linear function is $ \ y(t) = e^{x(t)} $
because the result of the 1st method above yields $ \ e^{ax(t)} + e^{bx(t)} $
and the result of the 2nd method above yields $ \ e^{ax(t) + bx(t)} $, which is not equal to the first result.