(→Part 2) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 44: | Line 44: | ||
== Part 2 == | == Part 2 == | ||
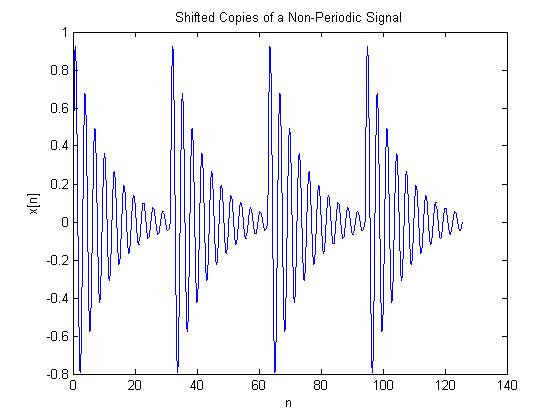
| − | If we use the function <math>x[n]=e^{-n/10}*sin(2n)</math> and add shifted copies of the signal together, we obtain | + | If we use the function <math>x[n]=e^{-n/10}*sin(2n)</math> and add shifted copies of the signal together, we obtain a periodic signal. |
| − | a periodic signal. | + | |
| + | Note: The exponent in the above equation was changed from -n/20 (from hw1) to -n/10 because it made the graph look better. | ||
<pre> | <pre> | ||
Latest revision as of 08:59, 12 September 2008
Part 1
Seems like a lot of people used the cosine function in hw1 so thats the one i'll use now.
%{
Jeremiah Wise
9/11/08
HW #2 Part A 1
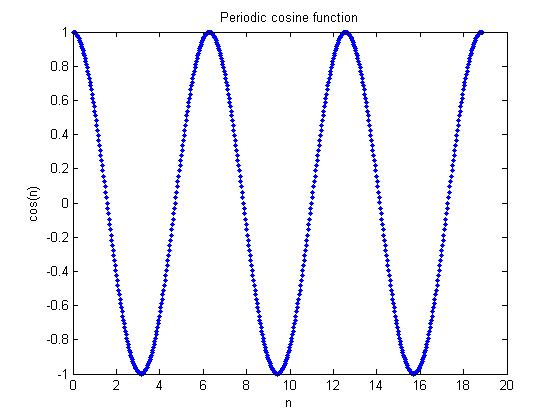
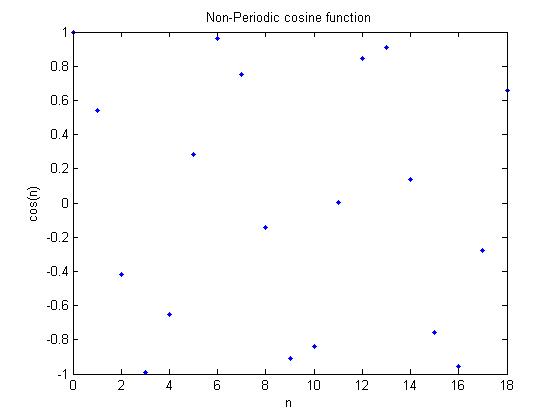
This program plots and displays a cosine wave
in DT. The first plot is periodic and the second
is not.
%}
%Periodic signal
delta = pi/100;
n = [0 : delta : 6 * pi];
plot(n, cos(n), '.');
title('Periodic cosine function');
xlabel('n');
ylabel('cos(n)');
%Non-Periodic Signal
figure(2)
delta = 1;
n = [0 : delta : 6 * pi];
plot(n, cos(n), '.');
title('Non-Periodic cosine function');
xlabel('n');
ylabel('cos(n)');
Part 2
If we use the function $ x[n]=e^{-n/10}*sin(2n) $ and add shifted copies of the signal together, we obtain a periodic signal.
Note: The exponent in the above equation was changed from -n/20 (from hw1) to -n/10 because it made the graph look better.
%{
Jeremiah Wise
9/12/08
HW #2 Part A 2
This program plots and displays a function that has been made periodic
by adding together shifted copies of that function.
%}
delta = 1 / 1000;
n = [0 : delta : 10 * pi];
x = exp(-n / 10) .* sin(2 * n);
for k = 1 : 1 : 2
n = [n (n + k*10*pi)];
x = [x x];
end
plot(n,x);
title('Shifted Copies of a Non-Periodic Signal');
xlabel('n');
ylabel('x[n]');