| (21 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Periodic CT Signal== | ==Periodic CT Signal== | ||
| − | + | From Homework 1: | |
<math>x(t)\;=\;sin(\frac{3}{4}t)</math> | <math>x(t)\;=\;sin(\frac{3}{4}t)</math> | ||
| − | Sampling the signal at a frequency that is | + | Sampling the signal at a frequency that is a rational multiple of the frequency of the signal will result in a periodic DT signal. Sampling the signal at a frequency that is not a rational multiple of the frequency of the signal will result in a non-periodic DT signal. |
| − | <math>2 | + | <math>2\pi f=\frac{3}{4}</math> |
<math>f=\frac{3}{8\pi}</math> | <math>f=\frac{3}{8\pi}</math> | ||
==Periodic DT Signal== | ==Periodic DT Signal== | ||
| − | Sampling the signal at a frequency (four times the original frequency ) | + | Sampling the signal at a frequency <math>f=\frac{3}{2\pi}</math> (four times the original frequency) yields a new frequency for the periodic DT signal <math>f_{DT}=\frac{1}{4}</math>, resulting in <math>x(t)=sin(\frac{1}{2}\pi t)</math>, which is clearly periodic (the repeating pattern: 0,1,0,-1,0,1,0). |
| + | |||
| + | ==Non-Periodic DT Signal== | ||
| + | Sampling the signal at a frequency <math>f=3</math> (<math>8\pi</math> times the original frequency) yields a new frequency for the periodic DT signal <math>f_{DT}=\frac{1}{8\pi}</math>, resulting in <math>x(t)=sin(\frac{1}{4}t)</math>, which is clearly non-periodic. There is no integer multiple of <math>\frac{1}{f_{DT}}=8\pi</math> that is also an integer. | ||
| + | |||
| + | ==Shifted Copies of a Non-Periodic Signal== | ||
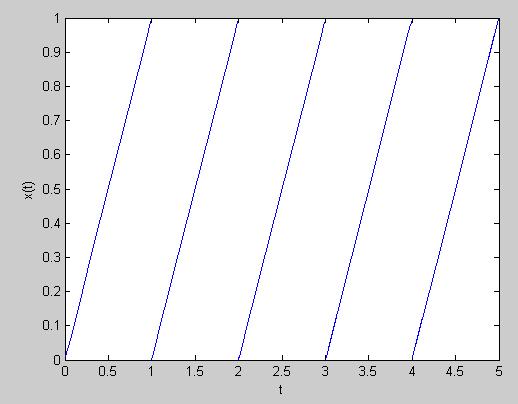
| + | A very obvious non-periodic signal from HW1 is <math>x(t) = t</math>. By concatenating an infinite number of shifted copies of <math>x(t)</math> together, the following signal is obtained: | ||
| + | |||
| + | [[Image:Rampsjp_ECE301Fall2008mboutin.JPG]] | ||
Latest revision as of 15:20, 11 September 2008
Contents
Periodic CT Signal
From Homework 1:
$ x(t)\;=\;sin(\frac{3}{4}t) $
Sampling the signal at a frequency that is a rational multiple of the frequency of the signal will result in a periodic DT signal. Sampling the signal at a frequency that is not a rational multiple of the frequency of the signal will result in a non-periodic DT signal.
$ 2\pi f=\frac{3}{4} $
$ f=\frac{3}{8\pi} $
Periodic DT Signal
Sampling the signal at a frequency $ f=\frac{3}{2\pi} $ (four times the original frequency) yields a new frequency for the periodic DT signal $ f_{DT}=\frac{1}{4} $, resulting in $ x(t)=sin(\frac{1}{2}\pi t) $, which is clearly periodic (the repeating pattern: 0,1,0,-1,0,1,0).
Non-Periodic DT Signal
Sampling the signal at a frequency $ f=3 $ ($ 8\pi $ times the original frequency) yields a new frequency for the periodic DT signal $ f_{DT}=\frac{1}{8\pi} $, resulting in $ x(t)=sin(\frac{1}{4}t) $, which is clearly non-periodic. There is no integer multiple of $ \frac{1}{f_{DT}}=8\pi $ that is also an integer.
Shifted Copies of a Non-Periodic Signal
A very obvious non-periodic signal from HW1 is $ x(t) = t $. By concatenating an infinite number of shifted copies of $ x(t) $ together, the following signal is obtained: