(→Examples) |
|||
| Line 20: | Line 20: | ||
</pre> | </pre> | ||
Therefore, this system is linear | Therefore, this system is linear | ||
| + | |||
| + | |||
| + | A Non-linear System: | ||
| + | |||
| + | <math> y(t) = x(t)^2 </math> | ||
| + | |||
| + | <pre> | ||
| + | x1(t) -> Ax1(t) | ||
| + | |+| Ax(t) + Bx(t) -System-> (Ax(t) + Bx(t))^2 | ||
| + | x2(t) -> Bx2(t) | ||
| + | |||
| + | x1(t) -System-> x1(t)^2 -> Ax1(t)^2 | ||
| + | |+| Ax1(t)^2 + Bx2(t)^2 | ||
| + | x2(t) -System-> x2(t)^2 -> Bx2(t)^2 | ||
| + | </pre> | ||
| + | |||
| + | Therefore, this system is non-linear | ||
Latest revision as of 11:14, 11 September 2008
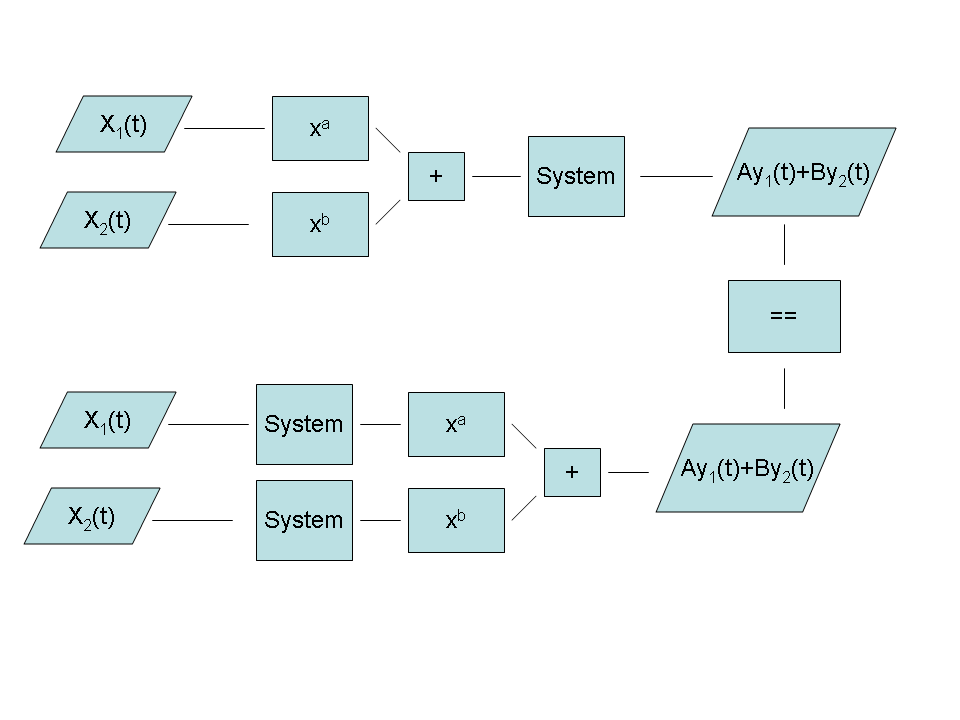
A system is called linear if:
Examples
A Linear System:
$ y(t) = 2x(2t) $
x1(t) -> Ax1(t)
|+| Ax(t) + Bx(t) -System-> 2Ax1(2t) + 2Bx2(2t)
x2(t) -> Bx2(t)
x1(t) -System-> 2x1(2t) -> 2Ax1(2t)
|+| 2Ax1(2t) + 2Bx2(2t)
x2(t) -System-> 2x2(2t) -> 2Bx2(2t)
Therefore, this system is linear
A Non-linear System:
$ y(t) = x(t)^2 $
x1(t) -> Ax1(t)
|+| Ax(t) + Bx(t) -System-> (Ax(t) + Bx(t))^2
x2(t) -> Bx2(t)
x1(t) -System-> x1(t)^2 -> Ax1(t)^2
|+| Ax1(t)^2 + Bx2(t)^2
x2(t) -System-> x2(t)^2 -> Bx2(t)^2
Therefore, this system is non-linear