(→Part 1) |
(→Part 2) |
||
| (17 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
<math>\,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\,</math> | <math>\,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\,</math> | ||
| − | + | is periodic, since | |
| − | <math>\,y[n]=y[n+ | + | <math>\,\exists N\in \mathbb{Z}, N\not= 0\,</math> such that <math>\,y[n]=y[n+N], \forall n\in \mathbb{Z}\,</math> |
| + | <math>\,2cos(\frac{2\pi n}{10})=2cos(\frac{2\pi n}{10}+\frac{2\pi N}{10})\,</math> | ||
| − | This can be seen in the following plot | + | This is true when |
| + | |||
| + | <math>\,\frac{2\pi N}{10}=2\pi \,</math> | ||
| + | |||
| + | <math>\,N=10\,</math> | ||
| + | |||
| + | |||
| + | This can be seen in the following plot: | ||
[[Image:Jkubasci dt periodic_ECE301Fall2008mboutin.jpg]] | [[Image:Jkubasci dt periodic_ECE301Fall2008mboutin.jpg]] | ||
| Line 26: | Line 34: | ||
<math>\,z[n]=x[\frac{n}{2\pi}]=2cos(n)\,</math> | <math>\,z[n]=x[\frac{n}{2\pi}]=2cos(n)\,</math> | ||
| − | + | is not periodic in DT, since there is no integer <math>N\in \mathbb{Z}, N\not= 0</math> such that | |
| − | This can be seen in the following plot | + | <math>\,z[n]=z[n+N], \forall n\in \mathbb{Z}\,</math> |
| + | |||
| + | <math>\,2cos(n)=2cos(n+N)\,</math> | ||
| + | |||
| + | This would be true when | ||
| + | |||
| + | <math>\,N=2\pi k, k\in \mathbb{Z}, k\not= 0\,</math> | ||
| + | |||
| + | <math>\,\frac{N}{k}=2\pi \,</math> | ||
| + | |||
| + | but, <math>2\pi</math> is irrational, thus there are no values for the integers <math>\,N,k\,</math> that will satisfy this equation. | ||
| + | |||
| + | This can be seen in the following plot: | ||
[[Image:Jkubasci dt nonperiodic_ECE301Fall2008mboutin.jpg]] | [[Image:Jkubasci dt nonperiodic_ECE301Fall2008mboutin.jpg]] | ||
== Part 2 == | == Part 2 == | ||
| + | The non-periodic function was chosen from HW1: [[HW1.4 Ben Horst_ECE301Fall2008mboutin]]. It appears to be possible with this function since the function decays in the positive and negative x directions. | ||
| + | |||
| + | <math>\,x(t)=\frac{sin(t)}{t}\,</math> | ||
| + | |||
| + | |||
| + | The function could be made periodic by: | ||
| + | |||
| + | <math>\,y(t)=\sum_{k\in \mathbb{Z}}x(t+2\pi k)=\sum_{k\in \mathbb{Z}}\frac{sin(t+2\pi k)}{t+2\pi k}\,</math> | ||
| + | |||
| + | |||
| + | '''Proof:''' | ||
| + | |||
| + | Need to show <math>\,\exists T\in \mathbb{R}, T\not= 0\,</math> such that | ||
| + | |||
| + | <math>\,y(t)=y(t+T), \forall t\in \mathbb{R}\,</math> | ||
| + | |||
| + | <math>\,\sum_{k\in \mathbb{Z}}\frac{sin(t+2\pi k)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t+T+2\pi k)}{t+T+2\pi k}\,</math> | ||
| + | |||
| + | <math>\,\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t+T)}{t+T+2\pi k}\,</math> | ||
| + | |||
| + | |||
| + | Choose <math>\,T=2\pi \,</math> | ||
| + | |||
| + | <math>\,\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t+2\pi )}{t+2\pi +2\pi k}\,</math> | ||
| + | |||
| + | <math>\,\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi (k+1)}\,</math> | ||
| + | |||
| + | |||
| + | With the infinite sum, there will be always be matching terms for the <math>k</math> and <math>k+1</math>, since we are covering all <math>k\in \mathbb{Z}</math> with the summation. Therefore, the two are equal and <math>\,y(t)\,</math> is periodic. | ||
Latest revision as of 05:47, 12 September 2008
Part 1
The function was chosen at random from HW1: HW1.4 Hang Zhang - Periodic vs Non-period Functions_ECE301Fall2008mboutin
$ \,x(t)=2cos(2\pi t)\, $
Periodic Signal in DT:
If $ x(t) $ is sampled at $ period=0.1 $, the function
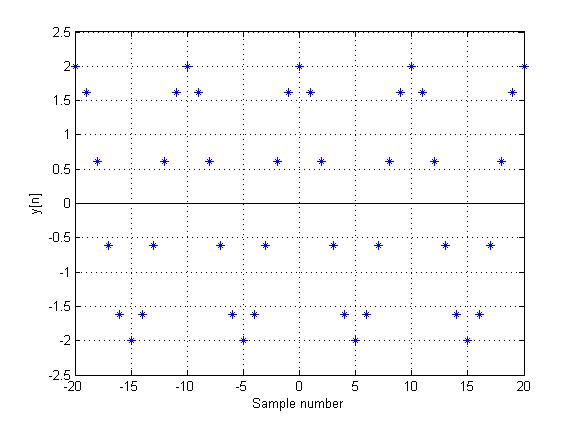
$ \,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\, $
is periodic, since
$ \,\exists N\in \mathbb{Z}, N\not= 0\, $ such that $ \,y[n]=y[n+N], \forall n\in \mathbb{Z}\, $
$ \,2cos(\frac{2\pi n}{10})=2cos(\frac{2\pi n}{10}+\frac{2\pi N}{10})\, $
This is true when
$ \,\frac{2\pi N}{10}=2\pi \, $
$ \,N=10\, $
This can be seen in the following plot:
Non-Periodic Signal in DT:
However, if $ x(t) $ is sampled at $ period=1/2\pi $, the function
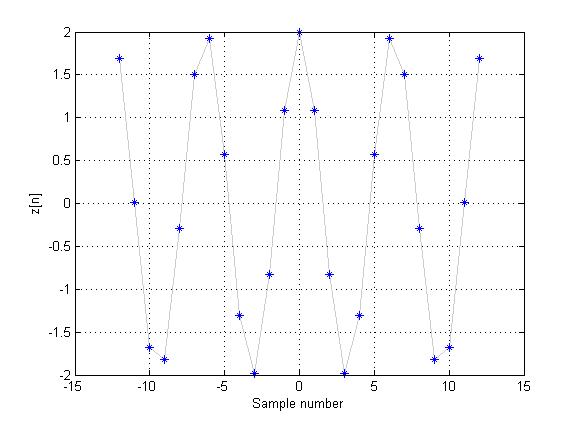
$ \,z[n]=x[\frac{n}{2\pi}]=2cos(n)\, $
is not periodic in DT, since there is no integer $ N\in \mathbb{Z}, N\not= 0 $ such that
$ \,z[n]=z[n+N], \forall n\in \mathbb{Z}\, $
$ \,2cos(n)=2cos(n+N)\, $
This would be true when
$ \,N=2\pi k, k\in \mathbb{Z}, k\not= 0\, $
$ \,\frac{N}{k}=2\pi \, $
but, $ 2\pi $ is irrational, thus there are no values for the integers $ \,N,k\, $ that will satisfy this equation.
This can be seen in the following plot:
Part 2
The non-periodic function was chosen from HW1: HW1.4 Ben Horst_ECE301Fall2008mboutin. It appears to be possible with this function since the function decays in the positive and negative x directions.
$ \,x(t)=\frac{sin(t)}{t}\, $
The function could be made periodic by:
$ \,y(t)=\sum_{k\in \mathbb{Z}}x(t+2\pi k)=\sum_{k\in \mathbb{Z}}\frac{sin(t+2\pi k)}{t+2\pi k}\, $
Proof:
Need to show $ \,\exists T\in \mathbb{R}, T\not= 0\, $ such that
$ \,y(t)=y(t+T), \forall t\in \mathbb{R}\, $
$ \,\sum_{k\in \mathbb{Z}}\frac{sin(t+2\pi k)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t+T+2\pi k)}{t+T+2\pi k}\, $
$ \,\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t+T)}{t+T+2\pi k}\, $
Choose $ \,T=2\pi \, $
$ \,\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t+2\pi )}{t+2\pi +2\pi k}\, $
$ \,\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi k}=\sum_{k\in \mathbb{Z}}\frac{sin(t)}{t+2\pi (k+1)}\, $
With the infinite sum, there will be always be matching terms for the $ k $ and $ k+1 $, since we are covering all $ k\in \mathbb{Z} $ with the summation. Therefore, the two are equal and $ \,y(t)\, $ is periodic.