(New page: == Part A, 1. == Using a CT signal that was posted in Homework 1, it is possible to create both a periodic and non-periodic DT signal, depending on what sampling frequency one chooses. Th...) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == Part A | + | == Part A: Periodic Signals Revisited == |
| − | + | By sampling a CT periodic signal at different frequencies, one can produce both a periodic and non-periodic DT signal. I chose to use the tangent signal from Homework 1. | |
| + | |||
:<center><math>\tan\theta = \frac{\sin\theta}{\cos\theta}\,</math></center> | :<center><math>\tan\theta = \frac{\sin\theta}{\cos\theta}\,</math></center> | ||
| Line 8: | Line 9: | ||
<center>[[Image:tangent_ECE301Fall2008mboutin.jpg]]</center> | <center>[[Image:tangent_ECE301Fall2008mboutin.jpg]]</center> | ||
| + | |||
| + | |||
| + | |||
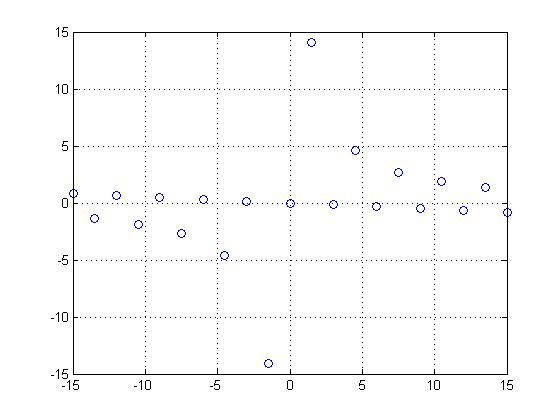
| + | By sampling the signal with x[n]=tan[k+n] and k=1.5, it is possible to produce a non-periodic DT signal. | ||
| + | |||
| + | <center>[[Image:tan_nonperiodic_ECE301Fall2008mboutin.jpg]]</center> | ||
| + | |||
| + | |||
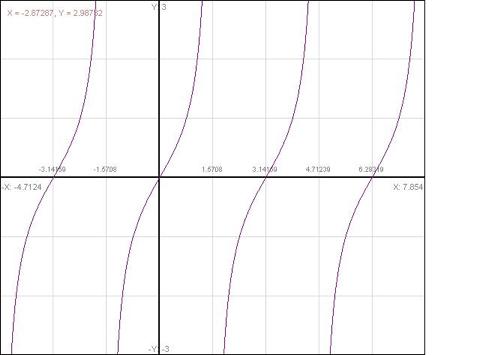
| + | By sampling the signal with x[n]=tan[k+n] and <math>k = {\pi\over 8}</math> | ||
| + | |||
| + | |||
| + | <center>[[Image:tan_periodic_ECE301Fall2008mboutin.jpg]]</center> | ||
| + | |||
| + | |||
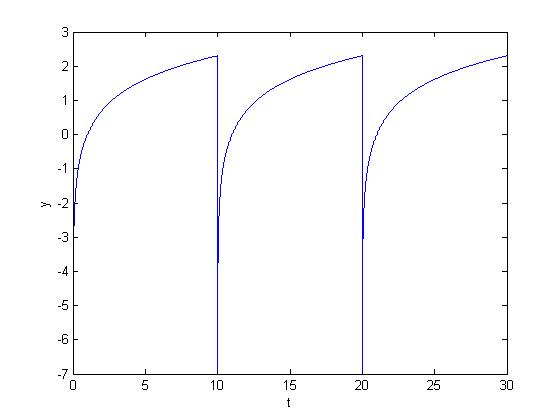
| + | One can also create a periodic signal by adding together an infinite number of shifted copies of a non-periodic signal periodically, either in CT or DT. I will use the natural logarithm function in CT to show this property. y=ln(x) | ||
| + | |||
| + | |||
| + | <center>[[Image:ln_periodic_ECE301Fall2008mboutin.jpg]]</center> | ||
Latest revision as of 09:46, 11 September 2008
Part A: Periodic Signals Revisited
By sampling a CT periodic signal at different frequencies, one can produce both a periodic and non-periodic DT signal. I chose to use the tangent signal from Homework 1.
$ \tan\theta = \frac{\sin\theta}{\cos\theta}\, $
By sampling the signal with x[n]=tan[k+n] and k=1.5, it is possible to produce a non-periodic DT signal.
By sampling the signal with x[n]=tan[k+n] and $ k = {\pi\over 8} $
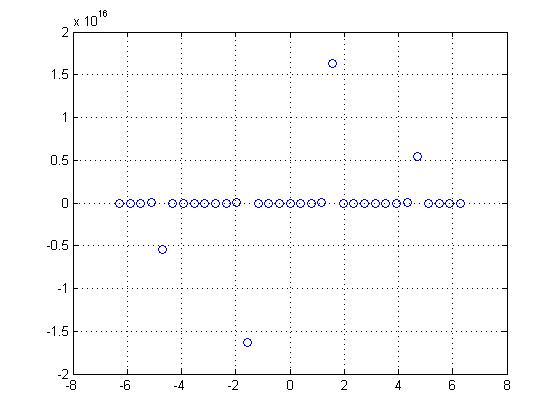
One can also create a periodic signal by adding together an infinite number of shifted copies of a non-periodic signal periodically, either in CT or DT. I will use the natural logarithm function in CT to show this property. y=ln(x)