(→Question 2) |
(→Question 2) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 43: | Line 43: | ||
and the plot | and the plot | ||
| − | [[Image: | + | |
| + | |||
| + | [[Image: Periodic_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 15:24, 11 September 2008
Question 1
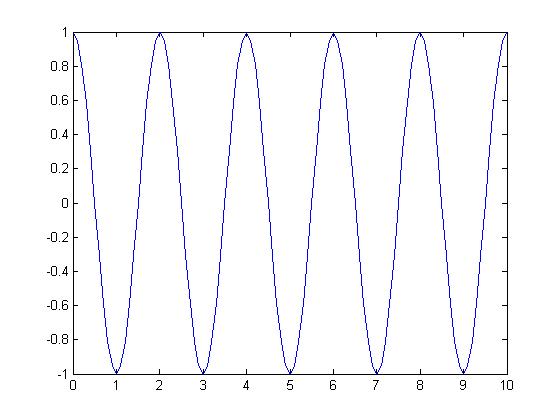
I chose the signal $ x[n]=e^{j\pi n} \, $ which Jeff Kubascik posted on his HW1.
Recall that this signal is periodic if $ T = {\omega_0\over2\pi}\, $ is rational.
Say I choose the sampling period $ T_s=.1\, $
The output will be:
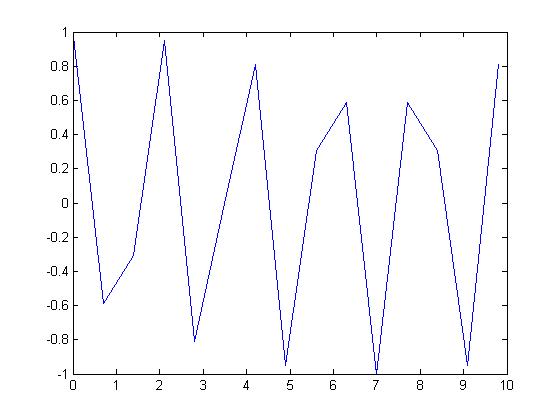
But if I choose the sampling period to be $ T_s=.7\, $
Question 2
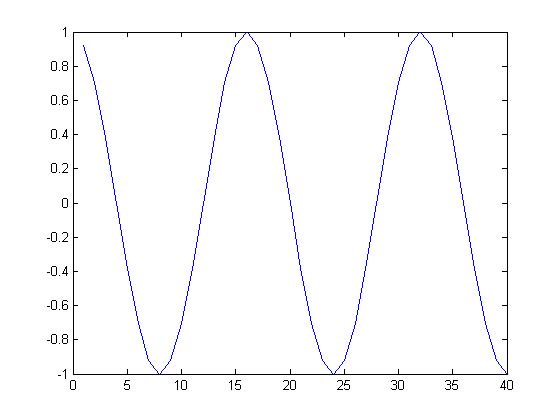
I'm including the code for this part because I found help using Tyler Houlihan's work. He apparently also received help from Wei Jian Chan's HW. I used Tyler's code as a base to recreate a periodic signal from:
$ e^{-t}sin(t)\, $
Here's the code:
%Creating 3 time vectors t=[0:0.001:1.5;0:0.001:1.5;0:0.001:1.5]; %setting the three variables, with their offsets y =exp(-t(1,:)).*sin(t(1,:)); y2=exp(-t(2,:)).*sin(t(2,:)); y3=exp(-t(3,:)).*sin(t(3,:)); %concatenating them, ie putting them after another y4=[y,y2,y3]; %making the new time axis for the whole thing t=0:0.001:4.502; %plotting plot(t,y4);
and the plot