(New page: == Part C: Linearity == A linear system is a system such that for any constants <math> a </math> and <math> b </math> on the complex plane, inputs <math> x(t) </math> and <math> y(t) </ma...) |
(→Part C: Linearity) |
||
| Line 2: | Line 2: | ||
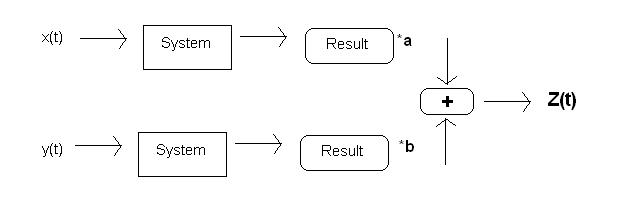
A linear system is a system such that for any constants <math> a </math> and <math> b </math> on the complex plane, inputs <math> x(t) </math> and <math> y(t) </math> produce the same <math> z(t) </math> no matter which of the following two paths they take through the system: | A linear system is a system such that for any constants <math> a </math> and <math> b </math> on the complex plane, inputs <math> x(t) </math> and <math> y(t) </math> produce the same <math> z(t) </math> no matter which of the following two paths they take through the system: | ||
| + | |||
| + | [[Image:Partc1_ECE301Fall2008mboutin.JPG]] | ||
Revision as of 15:35, 10 September 2008
Part C: Linearity
A linear system is a system such that for any constants $ a $ and $ b $ on the complex plane, inputs $ x(t) $ and $ y(t) $ produce the same $ z(t) $ no matter which of the following two paths they take through the system: