| (12 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
Solutions | Solutions | ||
| − | The Hydrogen Atom | + | The Hydrogen Atom and Atomic Theory |
Quantum Tunneling | Quantum Tunneling | ||
| Line 25: | Line 25: | ||
<center><math> \hat H \psi = E \psi</math></center> | <center><math> \hat H \psi = E \psi</math></center> | ||
| − | First postulated in 1925 by its namesake discoverer, Erwin | + | First postulated in 1925 by its namesake discoverer, Erwin Schrödinger, the Schrödinger equation is used to describe the wavefunction of particles – that is, an equation that unifies the wave and particle nature of the energy of matter. In its most simple form, it is expressed as a partial differential equation between its energy, representing the wave characteristic, and the Hamiltonian, describing its particle nature (Atkins 17). Depending on constraints, the Hamiltonian takes different values - we will be studying in detail the Hamiltonian for a relatively simple equation. The equation became the foundation for the field known today as quantum mechanics. Although expressible in many different forms, in this paper we limit our scope to perhaps the most famous and simple systems, the particle-in-a-box. We will then examine applications of the Schrödinger equation in atomic theory and quantum tunneling. |
== The Wavefunction == | == The Wavefunction == | ||
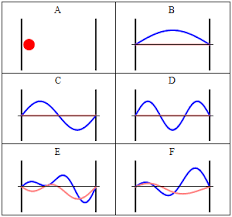
| − | + | In order to begin our exploration of the wonder of the Schrödinger equation, we must begin, (as always?), with definition. Central to the Schrödinger equation is the idea of a wavefunction, an equation which, very simply, takes on values based upon the position of the particle in question. Prior to Schrödinger's formulation, physicists had no way of describing both the particle and wave nature of particles in a single equation. Schrödinger's insight was to use the wavefunction as a wave analog to the precise momentum and directions of particles (after all, such terms are meaningless in waves). For our explicit investigation (and my sanity/calculus knowledge) we will limit our calculation to the 1D particle-in-a-box model, but we will discuss radial and angular wavefunctions as applied in hydrogenlike wavefunctions stemming from the Bohr model. | |
| − | In order to begin our exploration of the wonder of the | + | |
[[Image:download.png]] | [[Image:download.png]] | ||
| − | We use <math> \psi(x) </math> to represent a '''continuous''' wavefunction (abbreviated henceforth as <math> \psi </math>) , but what does it mean? Physically, a wavefunction has no direct significance; however, the '' Born '' interpretation of the wavefunction states the probability of finding a particle in a given region is proportional to the value of the wavefunction <math> \psi </math> squared. Indeed, <math> \psi^2 </math> is given its own definition as a probability density, which we have encountered before - the probability of finding the particle in the region divided by the region's volume. | + | We use <math> \psi(x) </math> to represent a '''continuous''' wavefunction (abbreviated henceforth as <math> \psi </math>) , but what does it mean? Physically, a wavefunction has no direct significance; however, the '' Born '' interpretation of the wavefunction states the probability of finding a particle in a given region is proportional to the value of the wavefunction <math> \psi </math> squared (Atkins 17). Indeed, <math> \psi^2 </math> is given its own definition as a probability density, which we have encountered before - the probability of finding the particle in the region divided by the region's volume. |
| − | |||
| − | |||
| − | |||
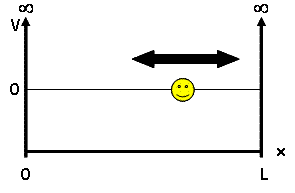
== Particle-in-a-box == | == Particle-in-a-box == | ||
| Line 45: | Line 41: | ||
[[Image:ParticleInABox.gif]] | [[Image:ParticleInABox.gif]] | ||
| − | So what, then, is our equation? We replace our hamiltonian <math> \hat H </math> with something a little more concrete, and | + | So what, then, is our equation? We replace our hamiltonian <math> \hat H </math> with something a little more concrete, and Schrödinger determines this time-independent equation to be: |
| − | <center><math> -\frac {h^2}{8m \pi^2} \frac {d^2\psi}{dx^2} + V(x)\psi = E\psi</math></center> | + | <center><math> -\frac {h^2}{8m \pi^2} \frac {d^2\psi}{dx^2} + V(x)\psi = E\psi</math> (Atkins 18) </center> |
But as we have just defined, our potential energy <math> V(x) </math> is 0 everywhere inside the box, leading us to the result | But as we have just defined, our potential energy <math> V(x) </math> is 0 everywhere inside the box, leading us to the result | ||
| Line 61: | Line 57: | ||
== Solutions == | == Solutions == | ||
| − | Armed with our new equation, we now attempt to determine our allowed wavefunctions. The solutions for this form of | + | Armed with our new equation, we now attempt to determine our allowed wavefunctions. The solutions for this form of Schrödinger's equation are well-documented, and are given in the form: |
<center><math> \psi(x) = A\sin kx + B\cos kx</math></center> | <center><math> \psi(x) = A\sin kx + B\cos kx</math></center> | ||
| Line 101: | Line 97: | ||
One of the most striking implications of this result is the variable <math> n </math>; as it can only take on integral values, the energy of the particle is '''quantized''', restricted to discrete values. This has profound implications for quantum mechanics - classically, a particle can take on a range of any amount of total energy; however, quantum mechanics dictates that, since only certain wavefunctions 'fit' inside the box, particles can only have certain energy levels. Included below is a link to a helpful tool that visualizes quantized energy levels in the particle in a box model: | One of the most striking implications of this result is the variable <math> n </math>; as it can only take on integral values, the energy of the particle is '''quantized''', restricted to discrete values. This has profound implications for quantum mechanics - classically, a particle can take on a range of any amount of total energy; however, quantum mechanics dictates that, since only certain wavefunctions 'fit' inside the box, particles can only have certain energy levels. Included below is a link to a helpful tool that visualizes quantized energy levels in the particle in a box model: | ||
| − | [ | + | [http://www.falstad.com/qm1d/ ParticleInABox] |
| + | |||
| + | ==The Hydrogen Atom and Atomic Theory== | ||
| + | |||
| + | Having completed our study into the wavefunction in 1D, we now turn to a 'more practical' application in atomic theory- the hydrogen atom. Instead of a box bound in 1 direction, we can think of an electron going about a nucleus as a particle, but bound in 3 dimensional space by the attraction at the center of the atom. Our wavefunctions, too, now reside in 3 coordinates - <math> r, \theta, \phi </math>, which we have met before as spherical coordinates. Each wavefunction now represents what is known as an atomic orbital - a quantized, discrete energy level which can be occupied by an electron. Each wavefunction can be written as a combination of 2 wavefunctions: the radial wavefunction <math> R(r) </math> and the angular wavefunction <math> Y(\theta, \phi)</math> (Atkins 22). Derivation of the wavefunctions from the time-independent is beyond the scope of this paper, but we will examine briefly the wavefunction corresponding to the ground state hydrogen atom ( <math> n = 1 </math>): | ||
| + | |||
| + | <center> <math> \psi (r, \theta, \phi) = \frac {e^{-r/a_{0}}}{(\pi (a_{0})^{3})^{1/2}} </math></center> | ||
| + | |||
| + | with <math> a_{0} </math> representing a mélange of fundamental constants known as the Bohr radius and equivalent to 52.9pm (Atkins 24). | ||
| + | |||
| + | Further wavefunctions for higher energy levels are more complex and are listed briefly in the table below: | ||
| + | |||
| + | <center> [[Image:WavefunctionTable.png]] </center> | ||
| + | |||
| + | These wavefunctions form the basis for atomic orbital theory as well as the accepted theory for electron distribution in subshells based upon quantum number. | ||
| + | |||
| + | ==Quantum Tunnelling== | ||
| + | |||
| + | Our final examination into a result of the Schrödinger equation is the phenomenon of quantum tunnelling. Recall our conditions for the particle-in-a-box system; we said that the particle was defined to exist between two '''impassable''' wells of infinite potential energy. Quantum tunnelling is the effect where a particle approaching a boundary manages to pass through this potential barrier. The reasoning for this comes from the interpretation of Schrödinger's wavefunction and from Heisenberg's uncertainty principle. We said that the square of the wavefunction defined a probability density where the particle may exist. The uncertainty principle states that both a particles' momentum and position cannot be known simultaneously. As a result, the probability of a particle appearing in a given space cannot be 1 (or 0) since that would define its position. If we attempted to set the particle's position (i.e. a probability of 1) we would need to set its momentum to <math> \infty </math>, a mathematical impossibility. Thus, we '''must''' acknowledge, however infinitesimal, the probability of the particle appearing on ('tunneling to') the other side of the barrier proportional to the inverse of the determination of its location - in other words, never for scales relevant to classical mechanics (Oregon 1). On a quantum scale, however, tunneling can (and does) occur frequently, and amazingly is the basis for several practical applications, including the scanning tunneling microscope which enables imaging of the smallest components of the atom. | ||
| + | |||
| + | |||
| + | == References and Further Readings== | ||
| + | |||
| + | Relevant Wikipedia Articles (images included) | ||
| + | |||
| + | [https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation Schrödinger equation] | ||
| + | |||
| + | [https://en.wikipedia.org/wiki/Quantum_tunnelling Quantum tunnelling] | ||
| + | |||
| + | Other texts used: (images from text as well) | ||
| + | |||
| + | Atkins, Peter, and Loretta Jones. Chemical Principles: The Quest for Insight. W H Freeman & Company, 2007. (particle-in-a-box) | ||
| + | |||
| + | Schiff, Leonard I. Quantum Mechanics. 1955. (Hydrogen Wavefunctions, 2nd chapter is a good introduction to the Schrödinger equation) | ||
| + | |||
| + | "Quantum Tunneling." University of Oregon. Accessed December 6, 2020. https://abyss.uoregon.edu/~js/glossary/quantum_tunneling.html. (Quantum Tunnelling) | ||
| + | |||
| + | [[Category:MA271Fall2020Walther]] | ||
Latest revision as of 19:34, 6 December 2020
Contents
Schrödinger Equation
Varun Chheda
Dr. Walther
Table of Contents
Introduction
The Wavefunction
Particle-in-a-box
Solutions
The Hydrogen Atom and Atomic Theory
Quantum Tunneling
References and Further Readings
Introduction
First postulated in 1925 by its namesake discoverer, Erwin Schrödinger, the Schrödinger equation is used to describe the wavefunction of particles – that is, an equation that unifies the wave and particle nature of the energy of matter. In its most simple form, it is expressed as a partial differential equation between its energy, representing the wave characteristic, and the Hamiltonian, describing its particle nature (Atkins 17). Depending on constraints, the Hamiltonian takes different values - we will be studying in detail the Hamiltonian for a relatively simple equation. The equation became the foundation for the field known today as quantum mechanics. Although expressible in many different forms, in this paper we limit our scope to perhaps the most famous and simple systems, the particle-in-a-box. We will then examine applications of the Schrödinger equation in atomic theory and quantum tunneling.
The Wavefunction
In order to begin our exploration of the wonder of the Schrödinger equation, we must begin, (as always?), with definition. Central to the Schrödinger equation is the idea of a wavefunction, an equation which, very simply, takes on values based upon the position of the particle in question. Prior to Schrödinger's formulation, physicists had no way of describing both the particle and wave nature of particles in a single equation. Schrödinger's insight was to use the wavefunction as a wave analog to the precise momentum and directions of particles (after all, such terms are meaningless in waves). For our explicit investigation (and my sanity/calculus knowledge) we will limit our calculation to the 1D particle-in-a-box model, but we will discuss radial and angular wavefunctions as applied in hydrogenlike wavefunctions stemming from the Bohr model.
We use $ \psi(x) $ to represent a continuous wavefunction (abbreviated henceforth as $ \psi $) , but what does it mean? Physically, a wavefunction has no direct significance; however, the Born interpretation of the wavefunction states the probability of finding a particle in a given region is proportional to the value of the wavefunction $ \psi $ squared (Atkins 17). Indeed, $ \psi^2 $ is given its own definition as a probability density, which we have encountered before - the probability of finding the particle in the region divided by the region's volume.
Particle-in-a-box
For our discussion, we will be looking at the particle-in-a-box model - a system which defines a particle of mass $ m $ and some potential energy $ V(x) $. This mass is placed into a 'box', a 1D universe of length $ L $ where potential energy is 0 inside the box but infinite outside, confining our particle to the inside of the box:
So what, then, is our equation? We replace our hamiltonian $ \hat H $ with something a little more concrete, and Schrödinger determines this time-independent equation to be:
But as we have just defined, our potential energy $ V(x) $ is 0 everywhere inside the box, leading us to the result
where $ h $ represents Planck's constant.
(We note that the term $ \frac {d^2\psi}{dx^2} $ is analogous to the curvature of the wavefunction!)
Before we go on to look at solutions to this equation, we must first ask what does this equation mean? Since we have defined our wavefunction across a universe ranging from 0 to $ V(x) $, its curvature basically represents its change in energy as it moves across its defined values. The negative sign is of great implication - as the 'value' of the potential energy of our wavefunction decreases, it is converted into kinetic energy. So even if our wavefunction curves downward measured across its potential energy, it represents a positive increase in its kinetic energy, heeding conservation. Consequently, the rate of change of energy - the curvature - is now interpreted to represent the momentum, implying its particle-like nature as well.
Solutions
Armed with our new equation, we now attempt to determine our allowed wavefunctions. The solutions for this form of Schrödinger's equation are well-documented, and are given in the form:
with $ A, B, $ and $ k $ constants.
We can verify this result by simply plugging the solution into the differential:
Substituting into our original equation gives
Indeed, we see that both the right and left hand sides of the equation are of the same form, and are equivalent if our constant $ k^2 = \frac{mE}{2\pi^2} $. As a result,
Having found our solution, we must still determine the values of our constants $ A, B, $ and $ k $ satisfying our constraints. Recall our initial condition: our particle cannot exist at either of the boundaries $ x = 0 $ or $ x = L $, so both $ \psi(0), \psi(L) = 0 $; this is only possible if $ B = 0 $. We now have
We use now our second boundary condition, $ L = 0 $. Since setting $ A = 0 $ makes our wavefunction 0 everywhere, we must impose another condition - in this case, we let $ kL = n\pi $, with $ n = 1, 2, 3, ... $
We now determine our final constant. Recall our definition of the probability density - the square of the wavefunction. Since the particle must exist inside the box, we have
The integral evaluates to $ \frac{L}{2} $, so $ A = (\frac{2}{L})^{\frac{1}{2}} $. We can now write our final wavefunction as
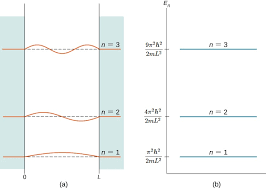
One of the most striking implications of this result is the variable $ n $; as it can only take on integral values, the energy of the particle is quantized, restricted to discrete values. This has profound implications for quantum mechanics - classically, a particle can take on a range of any amount of total energy; however, quantum mechanics dictates that, since only certain wavefunctions 'fit' inside the box, particles can only have certain energy levels. Included below is a link to a helpful tool that visualizes quantized energy levels in the particle in a box model:
The Hydrogen Atom and Atomic Theory
Having completed our study into the wavefunction in 1D, we now turn to a 'more practical' application in atomic theory- the hydrogen atom. Instead of a box bound in 1 direction, we can think of an electron going about a nucleus as a particle, but bound in 3 dimensional space by the attraction at the center of the atom. Our wavefunctions, too, now reside in 3 coordinates - $ r, \theta, \phi $, which we have met before as spherical coordinates. Each wavefunction now represents what is known as an atomic orbital - a quantized, discrete energy level which can be occupied by an electron. Each wavefunction can be written as a combination of 2 wavefunctions: the radial wavefunction $ R(r) $ and the angular wavefunction $ Y(\theta, \phi) $ (Atkins 22). Derivation of the wavefunctions from the time-independent is beyond the scope of this paper, but we will examine briefly the wavefunction corresponding to the ground state hydrogen atom ( $ n = 1 $):
with $ a_{0} $ representing a mélange of fundamental constants known as the Bohr radius and equivalent to 52.9pm (Atkins 24).
Further wavefunctions for higher energy levels are more complex and are listed briefly in the table below:

These wavefunctions form the basis for atomic orbital theory as well as the accepted theory for electron distribution in subshells based upon quantum number.
Quantum Tunnelling
Our final examination into a result of the Schrödinger equation is the phenomenon of quantum tunnelling. Recall our conditions for the particle-in-a-box system; we said that the particle was defined to exist between two impassable wells of infinite potential energy. Quantum tunnelling is the effect where a particle approaching a boundary manages to pass through this potential barrier. The reasoning for this comes from the interpretation of Schrödinger's wavefunction and from Heisenberg's uncertainty principle. We said that the square of the wavefunction defined a probability density where the particle may exist. The uncertainty principle states that both a particles' momentum and position cannot be known simultaneously. As a result, the probability of a particle appearing in a given space cannot be 1 (or 0) since that would define its position. If we attempted to set the particle's position (i.e. a probability of 1) we would need to set its momentum to $ \infty $, a mathematical impossibility. Thus, we must acknowledge, however infinitesimal, the probability of the particle appearing on ('tunneling to') the other side of the barrier proportional to the inverse of the determination of its location - in other words, never for scales relevant to classical mechanics (Oregon 1). On a quantum scale, however, tunneling can (and does) occur frequently, and amazingly is the basis for several practical applications, including the scanning tunneling microscope which enables imaging of the smallest components of the atom.
References and Further Readings
Relevant Wikipedia Articles (images included)
Other texts used: (images from text as well)
Atkins, Peter, and Loretta Jones. Chemical Principles: The Quest for Insight. W H Freeman & Company, 2007. (particle-in-a-box)
Schiff, Leonard I. Quantum Mechanics. 1955. (Hydrogen Wavefunctions, 2nd chapter is a good introduction to the Schrödinger equation)
"Quantum Tunneling." University of Oregon. Accessed December 6, 2020. https://abyss.uoregon.edu/~js/glossary/quantum_tunneling.html. (Quantum Tunnelling)