| (One intermediate revision by the same user not shown) | |||
| Line 44: | Line 44: | ||
| − | <center>[[Image:pythag_proof. | + | <center>[[Image:pythag_proof.png]]</center> |
| Line 85: | Line 85: | ||
| − | <center> | + | <center>[[Image:number_variable_thing.jpg]]</center> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 01:05, 6 December 2020
GÖDEL’S FIRST THEOREM
Gödel’s first incompleteness theorem is most simply stated as follows:
“There exists no sufficiently expressive system that is consistent and in which all statements that can be formed by that system can be proven true.”
Additionally, the inverse of this theorem is true. This theorem and its inverse contains many important terms that must be discussed and defined before moving on to a proof of the theorem.
1.1 Systems
To understand Gödel’s first theorem the term “system” must be defined. In the context of Gödel, a system is a set of rules or axioms. All systems, like math, are composed of a set of rules or axioms that define the system. The most commonly known set of axioms in mathematics are Peano Arithmetic. Peano Arithmetic refers to the math that is related to the most intuitive of axioms. A few examples of the Peano Arithmetic axioms are listed here:
x=x If x=y then y=x If x=y and x=z then z=y x+y=y+x
x*(1+y)=xy+x
Proofs can be done in this system to prove, for example, 1+1=2 is true because of these axioms. Mathematics as a field is defined by a larger set of axioms than simple Peano Arithmetic. However, it is important to realize that a different system can be imagined which has the axioms that pi is equal to 5 and if x=y then y≠x. Such a system would be chaotic and useless, but a reminder that a system is as it is chosen to be defined.
Henceforth, for purposes of this discussion, a mathematical system should be understood as a set of rules or axioms that govern mathemetics.
1.2 Consistent/Consistency
Consistency is a description of a system. If a system is consistent then all statements made in that system can be proven true by the axioms of the system, and must not be proven false by the axioms. A simple example of an inconsistent system would be one with the following axioms:
If x=y and x=z then z=y If x=y then y≠x
In this system any number would be both equal to itself and not, and both realities are true using the same set of axioms. This is inconsistent.
Consistency simply refers to the lack of contradiction in a system. A system that is consistent contains no statements that are both true and untrue using the same set of axioms.
1.3 Sufficiently Expressive System
A sufficiently expressive mathematical system is one that can be formed into something that can be fully understandable. In simple terms, if the axioms can be written and checked by a computer they are sufficiently expressive. To be sufficiently expressive, the written or spoken statements are adequate to describe the system fully. Likewise, each step of any proof should be done using the axioms or a derivation of them.
For example, the following is a proof of the Pythagorean theorem:
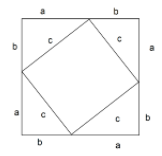
From this image the statement can be made that:
c2=a2+b2+2ab-2ab
c2=a2+b2
This proof can be understood in the context of axioms, as each step of this proof uses the axioms or their derivations. The first uses the identity for both the area of a square, and triangle to formulate an equation to describe the area of the innermost square. The next steps use simple axioms of arithmetic to derive the Pythagorean theorem.
Is it also true that a system that cannot express all of its rules and axioms so that they are understandable is not sufficiently expressive. The expression is insufficient.
All of mathematics is based on the idea that math is sufficiently expressive, all statements that are proven to be true because the steps to their proof are based on the axioms and their derivations.
1.4 Provable and completeness
The most sweeping part of Gödel’s incompleteness theorem is his proof that in any consistent system there exists true statements that cannot be proven. He proves that for any completely consistent set of axioms there are statements which are true, but for which no proof exists. He also maintains that all false statements can be proven false, as they have a counter example. A seemingly promising way to avoid this would be to make statements that are true, but cannot be proven true, to be axioms. Sadly, Gödel’s theorem still applies. If a statement that is true but cannot be proven true becomes an axiom, and the axioms remain consistent, then mathematics has not changed according to Gödel. The new set of axioms will still not be able to prove that all true statements are true.
The idea that there exist and will always exist statements within mathematics that are true but which don’t have a proof is known as incompleteness. A system in which all statements can be proven is complete. Because mathematics is presumed to be consistent, its incompleteness can best be thought of using the following analogy:
Mathematics is best thought of as a tree in an infinite forest whose roots are the axioms and branches and leaves are true statements. Proofs in this analogy are paths that an ant could take that lead to a branch or leaf. Some paths are longer than others, but all of them stay on the tree. If there exists a branch or leaf on an adjacent tree that is just out of reach. This leaf can be thought of as an unprovable true statement. The ant cannot jump from one tree to the next. If the leaf falls to ground and becomes part of the roots (i.e. the axioms) the tree may grow larger but is still not as big as the forest and never will be.
1.5 Inverse
The inverse of Gödel’s theorem is also true: If a mathematical system is complete it is not consistent. Gödel proved that this is the case and for standard mathematics incompleteness is far more preferable. One of the most enjoyable parts of math is that something is either wrong or right. If that is not the case then such a mathematical system is useless as statements that are incorrect and correct have no mathematical meaning. Mathematics' best application is to the physical world and a system that describes the physical world that is inconsistent is dangerous. The cables supporting a bridge cannot be both strong enough and not strong enough, the bridge either stands or it doesn’t. Luckily, it is widely accepted that mathematics is consistent as Gödel’s theorem proves that there are two realities: consistency and completeness, no system can have both. Several Mathematical statements have been shown to have no proof, but aren’t false.
1.6 Gödel’s proof
The following is a proof that a consistent mathematical system must be incomplete using the following steps:
Suppose a set of numbers which describe all mathematical operators and numbers. For example:
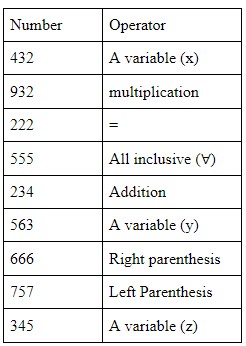
Using this system formulas can simply be written as a string of number with a zero separating each term:
Note that now every formula and identity in a sufficiently expressive system like the one shown has a unique number that corresponds to that exact formula and Identity. Similarly, any proof of an identity can be represented by a listable sequence of numbers. Gödel, using this numbering, makes the conclusion that there are a countably infinite number of valid proofs. This is the important distinction Gödel makes as now there is a numerical method by which all proofs and statements can be listed and checked for accuracy making mathematics sufficiently expressive.
The most commonly accepted proof of Gödel’s first incompleteness theorem and its inverse is the halting problem. The halting problem has strong references to computer science. Gödel first proposed his theorems in the 1930s, well before computer science existed. The Halting Problem will be discussed later. Gödel proved his theorem using logic.
To prove Gödel’s first theorem using logic one must propose the statement:
This statement will have a number, similar in construction to the example above. Likewise, this statement like any other must be correct or incorrect. If one makes the assumption that the statement is incorrect then the statement is assumed provable. However, a statement that is provable must be true. Thus a contradiction has arisen, as a statement that is presumed false has been proven true. If a mathematical statement can both be named false and true then the system in which exists is inconsistent.
If one makes the assumption that the statement is true and therefore it cannot be proven true then the system in which the statement exists is incomplete.
An issue one could take with this proof is that such a statement could be impossible to construct, this is untrue. The logic of the proof still holds. The analysis of a mathematical system here is done from the outside looking in. Meaning that a statement can be unprovable simply by the nature of the selection of a system. Recall, that if an unprovable statement is added to the axioms to create a new system it does not affect the system’s completeness. Just as before, if observing the system from afar another statement can be proposed that is true and unprovable and the new system is incomplete.
By the proposal of this statement Gödel’s first theorem has been proven true:
The inverse has also been proven true. This creates an existential crisis for mathematics as now it is either consistent or complete, it cannot be both.
For more information and a more complete proof of Gödel’s First Theorem, see source 4.

