| Line 5: | Line 5: | ||
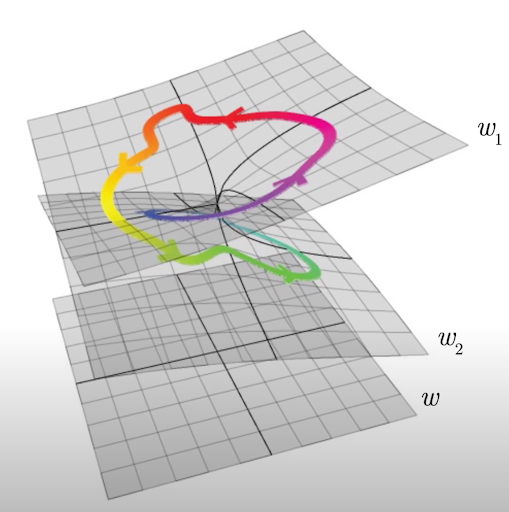
So what exactly are Riemann Surfaces? When one searches on the internet “Riemann Surfaces”, he is greeted with a picture of a very twisted space sitting in a 3-dimensional space. At first, the whole topic seems extremely daunting and incomprehensible, but when broken down, they are not as difficult to understand as one may have originally thought. By definition, a Riemann Surface is a Hausdorff Space that is connected by a complex structure. This surface has an atlas, as mentioned before as a transition map between two spaces, where the different points translate to two points on the higher-dimension complex plane. This idea can be better visualized like this: | So what exactly are Riemann Surfaces? When one searches on the internet “Riemann Surfaces”, he is greeted with a picture of a very twisted space sitting in a 3-dimensional space. At first, the whole topic seems extremely daunting and incomprehensible, but when broken down, they are not as difficult to understand as one may have originally thought. By definition, a Riemann Surface is a Hausdorff Space that is connected by a complex structure. This surface has an atlas, as mentioned before as a transition map between two spaces, where the different points translate to two points on the higher-dimension complex plane. This idea can be better visualized like this: | ||
| − | [[File:Surfaces1.png|framed|center]] | + | [[File:Surfaces1.png|255px|framed|center]] |
The colorful line represents the function that spans the Riemann Surface. The inputs for the function are on the plane-''w'' which consists of a real and imaginary axis. This plane is only two dimensions. The two planes above ''w'' are known as ''branches''. A value will be inputted into w and by a complex atlas, meaning a transition function, will take this value and translate it to where it lies on the branches. This function is also one-to-one and continuous which is an important idea since the domain will make up this curved surface in a higher dimensional space. This makes the once 2-dimensional surface in w greater than 2-dimensions and forms a complex surface. When all these points come together, they form a Riemann Surface. | The colorful line represents the function that spans the Riemann Surface. The inputs for the function are on the plane-''w'' which consists of a real and imaginary axis. This plane is only two dimensions. The two planes above ''w'' are known as ''branches''. A value will be inputted into w and by a complex atlas, meaning a transition function, will take this value and translate it to where it lies on the branches. This function is also one-to-one and continuous which is an important idea since the domain will make up this curved surface in a higher dimensional space. This makes the once 2-dimensional surface in w greater than 2-dimensions and forms a complex surface. When all these points come together, they form a Riemann Surface. | ||
Revision as of 22:39, 5 December 2020
What Are RiemannSurfaces?
So what exactly are Riemann Surfaces? When one searches on the internet “Riemann Surfaces”, he is greeted with a picture of a very twisted space sitting in a 3-dimensional space. At first, the whole topic seems extremely daunting and incomprehensible, but when broken down, they are not as difficult to understand as one may have originally thought. By definition, a Riemann Surface is a Hausdorff Space that is connected by a complex structure. This surface has an atlas, as mentioned before as a transition map between two spaces, where the different points translate to two points on the higher-dimension complex plane. This idea can be better visualized like this:
The colorful line represents the function that spans the Riemann Surface. The inputs for the function are on the plane-w which consists of a real and imaginary axis. This plane is only two dimensions. The two planes above w are known as branches. A value will be inputted into w and by a complex atlas, meaning a transition function, will take this value and translate it to where it lies on the branches. This function is also one-to-one and continuous which is an important idea since the domain will make up this curved surface in a higher dimensional space. This makes the once 2-dimensional surface in w greater than 2-dimensions and forms a complex surface. When all these points come together, they form a Riemann Surface. This fits with the original definition and makes it more comprehensive. Essentially, a Riemann Surface is a surface sitting in the complex plane, which is sometimes hard to visualize given that people do not know exactly what “imaginary” numbers are and what they are supposed to look like. Clearly, the definition is more complex than that, however to simplify this idea, it is easier to think of a Riemann Surface in this way.