| (16 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Application of Leibniz's Rule in Electrostatics= | =Application of Leibniz's Rule in Electrostatics= | ||
| − | From what we've seen about the Feynman/Leibniz rule of integration, we now have an additional method of | + | From what we've seen about the Feynman/Leibniz rule of integration, we now have an additional method of integration that will be assist us in finding solutions for various complex integrals that would have been more difficult to solve before. This, however, doesn't apply solely to the field of mathematics. Since many areas of study utilize the helpfulness of integrating and calculating values through derivates, it can be assumed that they will also benefit a lot from the Feynman technique. Physics in particular has a lot of use for these concepts, with velocity and acceleration being important aspects of the field, and its use continues throughout the rest of the topics. For example, one of these topics is electrostatics, which deals with the idea of calculating electric potential of a particle. |
| − | [[Image:Point_charge.png]] | + | <center>[[Image:Point_charge.png]]</center> |
| + | |||
| + | The simple equation for finding this potential would be <math> V = \frac{kq}{r} </math>, where ''k'' is the electrostatic constant, ''q'' is the charge of the particle, and ''r'' is the distance from the source and the particle. Although calculating the potential for single particles is quite straightforward, the process becomes more complex as we try and solve for ''V'' along different surfaces. Primarily, calculating the potential along rings or discs will involve a variation of integrating the electric potential equation (with other surface area formulas) along these surfaces. | ||
| + | With so many equations that create relationships between values, there are many ways for us to create functions to use with Feynman's rule. | ||
| + | To show an example, a common equation that relates electric field and electric potential is: | ||
| + | <center><math> E = -\nabla V </math></center> | ||
| + | The major takeaway from Feynman/Leibniz's rule is setting a function equal to an integral so that we can differentiate with respect to another variable, leaving an easier expression to integrate. With this equation above, there is a multitude of ways to set ''E'' equal to a function represented by the gradient multiplied with the integral that we get from electric potential. Now, with a new function representing this relationship between ''E'' and ''V'', we can use Feynman's rule to manipulate the gradient and potential integral so that we can solve the solution in an easier way. | ||
[[ Walther MA271 Fall2020 topic14 | Back to Feynman Integrals]] | [[ Walther MA271 Fall2020 topic14 | Back to Feynman Integrals]] | ||
[[Category:MA271Fall2020Walther]] | [[Category:MA271Fall2020Walther]] | ||
Latest revision as of 17:22, 4 December 2020
Application of Leibniz's Rule in Electrostatics
From what we've seen about the Feynman/Leibniz rule of integration, we now have an additional method of integration that will be assist us in finding solutions for various complex integrals that would have been more difficult to solve before. This, however, doesn't apply solely to the field of mathematics. Since many areas of study utilize the helpfulness of integrating and calculating values through derivates, it can be assumed that they will also benefit a lot from the Feynman technique. Physics in particular has a lot of use for these concepts, with velocity and acceleration being important aspects of the field, and its use continues throughout the rest of the topics. For example, one of these topics is electrostatics, which deals with the idea of calculating electric potential of a particle.
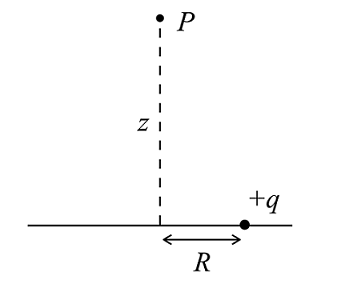
The simple equation for finding this potential would be $ V = \frac{kq}{r} $, where k is the electrostatic constant, q is the charge of the particle, and r is the distance from the source and the particle. Although calculating the potential for single particles is quite straightforward, the process becomes more complex as we try and solve for V along different surfaces. Primarily, calculating the potential along rings or discs will involve a variation of integrating the electric potential equation (with other surface area formulas) along these surfaces. With so many equations that create relationships between values, there are many ways for us to create functions to use with Feynman's rule. To show an example, a common equation that relates electric field and electric potential is:
The major takeaway from Feynman/Leibniz's rule is setting a function equal to an integral so that we can differentiate with respect to another variable, leaving an easier expression to integrate. With this equation above, there is a multitude of ways to set E equal to a function represented by the gradient multiplied with the integral that we get from electric potential. Now, with a new function representing this relationship between E and V, we can use Feynman's rule to manipulate the gradient and potential integral so that we can solve the solution in an easier way.

